大前提
基本的に大学生は遊ぶものだと考えています。勉強だけでなく、サークル、課外活動に精を出した方が、後々の就活、人間関係が豊かになります。
管理人も、学生時代は遊び惚けていました。
ただ一方で、大学受験で満足いく成果が得られなかった方もいらっしゃると思います。そのような場合、大学院で上のレベルの大学にチャレンジしたい思いもあるかもしれません。
そこで、本記事では、いわゆる学歴ロンダリングを狙う大学生が、ロンダを実現するために必要な春休みの勉強内容を学年別に解説していきます。
対象者

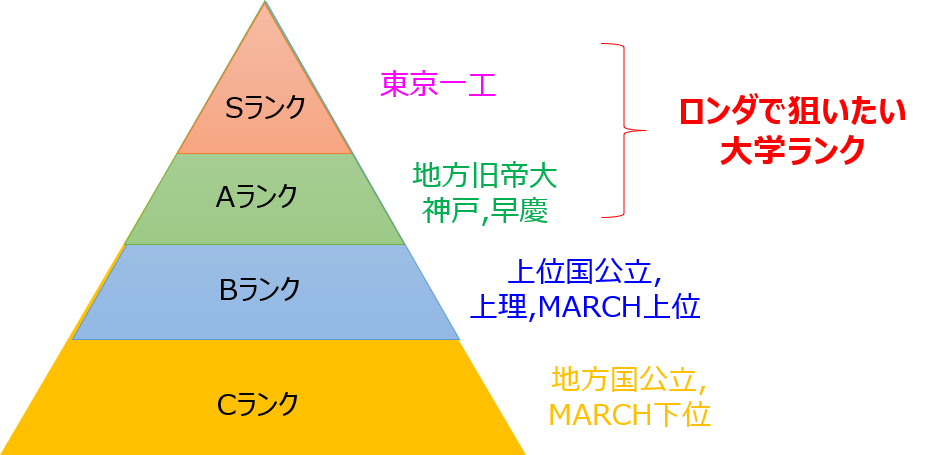
- Bランク以下の大学(旧帝一工+神戸+早慶以外)に通う学生 (高専上位でも可)
- Aランク以上の大学(旧帝一工+神戸+早慶)の大学へ院進を希望している
- 高校数学の基本問題は解けるレベル
- 大学の講義の単位取得状況はぼちぼち(留年していなければ良い。)
AランクとBランクで境界を分けたことには意味があります。
①大企業への就職で優遇されやすいから。
②アカポス(研究職)に就きやすいから。
以上2つの理由が大きいです。それぞれ下記で解説していきます。
大企業への就職について
筆者は東証一部企業を2社経験していますが、どちらの企業もAランク以上の大学出身者が全体の7割を占めています。(Bランクで3割弱、それ以下は若干数)
旧帝一工+神戸+早慶で全体12校ありますが、それだけで大枠を占めるという状況です。Bランクは30校程度ありますが、この中で全体の3割を取りに行かねばなりません。一般的に、Bランクになった途端競争が激しくなることが多いです。
大企業では、Aランク以上の大学は採用予定人数に個別で枠を設けられていることが多いです。そのため、競争すべき人数が少なくなります。
このような都合から、外部の大学へ院進を考える際は、積極的にAランク大学以上を目指した方が良いです。
補足
上記は、大企業の中でもメーカー、インフラ就職を志す学生向けに対しての言葉です。今人気のコンサルを目指す場合は、東京一工+早慶を狙った方が良いです。
ただし、早慶は私立であり、京大は関東の大学と比較して門戸が広くないです。よって、東大と東工大を狙うことが現状の最適解になりそうです。
また、どうしても学科による就職難易度の違いはあります。機電系、情報系ならば、Bランク以下の大学でも希望すれば大企業へ就職できる可能性は高いです。一方で、バイオ系だとSランクの大学でも厳しい場合があります。
ただ、本ブログは電気情報系の学生を対象としたものになります。よって、少なくとも工学部に属している前提で話を進めていきます。
アカポスへ就きやすさについて
これは言うまでもないでしょう。旧帝大+東工大では、研究予算、設備に大変恵まれています。筆者が通っていた東北大も環境に恵まれていました。
他大学では設備の都合で出来ない実験も、上記の大学ならば可能なことが多くなります。当然成果が出やすくなり、将来のアカポスへの近道になります。実際、大学教授の学歴を確認すると、旧帝大+東工大出身者が非常に多いです。
Bランク以下の大学に通う学生で研究職に就きたい方が居れば、大学院入試は最後のチャンスになるでしょう。
具体的な勉強内容
かつては難しい説明が多かった大学の教科書も、最近は分かりやすいものが増えました。書店に赴けば、初学者向けの参考書は多々あります。
全学年共通として、誰かに教えてもらう受け身の姿勢では無く、自身で勉強し、道を切り開いていくことが重要です。
学部1年(新2年)
一般教養で線形代数、微分積分の履修が完了し、大学次第では微分方程式、応用数学(複素関数、ラプラス変換)もかじっている場合もあります。
目指す大学が決まっていない場合が殆どですが、筆者としては電磁気学、電気回路の勉強をオススメします。(特に、電気系のコースへ進む学生)
理由は、殆どの大学の院試で出題されるからです。勉強してみたが、結局院試で使わなかった。という結末がほぼありません。
電磁気学を勉強する上での注意点
初学者には、ベクトル解析の知識不足が壁になります。微積分に向きの概念が生まれただけですが、最低限の計算ができるように勉強した方が良いかもしれません。院試で選択することをここでは想定しないため、下記のような教科書で十分と考えます。
電磁気学については、下記の1冊をオススメします。説明自体は他教科書でも良いかもしれませんが、演習問題の選定が非常に良いです。定期試験、院試で出題されやすい問題をピンポイントで当てていて、詳細に解説しています。試験で点を取るための教科書に向いています。
電気回路を勉強する上での注意点
フェーザ表示の単元の勉強をオススメします。電気回路を勉強し始めると、序盤で出てくる分野になります。コイル、コンデンサ成分を複素数で表す概念さえ理解すれば、後は高校数学の内容で勉強できます。余裕があれば二端子対回路も勉強できれば、学部2年以降楽になります。過渡現象については微分方程式色が強いので、学部2年からの勉強で問題無いです。
初学者向けに1冊だけ本をオススメするならば、管理人としては下記を推します。
新しい電気回路上下 松澤 昭 (著) (オススメ)
情報系の学生に対して
情報系の場合、電磁気、回路を始めとした物理学よりも、数学系の科目の比重が高いことが多いです。そのため、先の分野を勉強するよりも、線形代数、微積分の勉強を深めた方が良い可能性があります。
教科書自体は大学指定のものを既に購入済みだと思いますので、ここでは演習書を紹介します。
詳解と演習大学院入試問題 海老原 円 (著), 太田 雅人 (著)
もし先の勉強へ進まれるなら、論理回路、計算機学、アルゴリズム論をオススメします。論理回路は、高校までに習った関数が0,1出力する場合を考えれば良いです。計算機学に関しては、昨今のPC、スマホブームで基本的な構成は既にご存じかもしれません。アルゴリズム論は、プログラミングをする際に自然に勉強する分野です。どの科目を勉強しても、他科目との親和性が高いです。
下記に管理人がオススメする本を貼ります。
OHM大学テキスト 論理回路 今井正治 (著, 編集)
もしかすると初学者には難しいかもしれません。ただし、論理回路の科目自体の難易度は易しいと管理人は考えています。関数が0,1しか出力しないルールにさえ慣れてしまえば、↑の教科書も読み進めることができると期待しての紹介です。
コンピュータアーキテクチャ(改訂5版) 馬場敬信 (著)
分厚いですが、他教科書で院試向きのものがあるのかと聞かれると厳しいです。よって、上記の本を紹介します。全て読むことは難しいため、パイプライン、2進数の処理など、頻出分野を読み込む辞書的な使い方をオススメします。
Cによるアルゴリズムとデータ構造(改訂2版) 茨木 俊秀 (著)
他の記事でも紹介していますが、初学者でも使用できる内容です。薄すぎず、厚すぎずの分量で、勉強しやすいです。
学部2年(新3年)
専門科目を本格的に習いだし、ひと段落付いた頃だと思います。科目を絞れば、学部2年までに勉強した科目だけで受験できる大学院も出てきます。
ここでは、受験する大学院を数校に絞ることをオススメします。大学入試と同じく日程的に重複する大学も多く、そう何校も受験できないからです。
下記に、大学院ごとの受験日程を示します。
| 大学名 | 試験日程 (2024年実績) |
| 東京大学 | 24/8/26 ※電気系 |
| 京都大学 | 24/8月上旬 ※情報学研究科 |
| 東京工業大学 | 24/8/16 |
| 大阪大学 | 24/8/20~22 |
| 名古屋大学 | 24/8/20~21 |
| 東北大学 | 24/8/27~29 |
| 九州大学 | 24/9/10~11 |
| 北海道大学 | 24/8/27 |
受験する大学院を絞れれば、受験科目で未履修のものが含まれていないか確認しましょう。学部2年の春休みでは、未履修分野を減らす作業に終始した方が良いです。
下記の科目は様々な大学の院試で出題されやすいです。完了していないときは、この春休みで仕上げておくと後々楽です。
電気系科目
電子回路、半導体デバイス、制御工学、量子力学
後段の「選択をオススメする科目」の項にも出てきますが、電子回路、半導体デバイスを早いうちから得点源にしておくと良いです。オススメ教科書は下記です。
半導体デバイス (series電気・電子・情報系 7) 松波 弘之 (著), 吉本 昌弘 (著)
情報系科目
アルゴリズム論、計算機学、情報数学、オートマトン、情報論理学
大学2年の項目で紹介した3科目が核となりますが、情報数学も保険で勉強して良いかもしれません。下記に管理人のオススメ教科書を貼ります。
例題と演習でわかる離散数学 加納 幹雄 (著)
学部3年(新4年)
この学年は勉強を頑張った方が良いです。心配性な内部生も勉強を始めるからです。実際、周りと差が付きづらくなる時期です。
また、ここからは合格点を取る勉強に終始した方が良いです。点数を取りやすい科目に時間を振り、取りづらい科目については最低限の勉強にする濃淡が必要です。
下記に、筆者のオススメ順に科目を並べました。
電気系科目
上に行くほどオススメ
- 電子回路(大変オススメ)
- 電磁気学
- 半導体デバイス
- 量子力学
- 電気回路
- 信号処理
- 制御工学(古典制御のみ)
- 応用数学(フーリエ変換、複素関数、ラプラス変換)
- 一般教養の数学(線形代数、微分積分)
別の記事で科目ごとの特徴を詳しく述べようと思いますが、電子回路を特にオススメします。出題パターンが非常に限られており、回路の計算量も少ないことが多いです。=計算ミスのリスクも少なく、最も得点が安定しやすいです。
下に行くにつれて、計算量が多い科目を並べています。試験での計算ミスのリスクが高いことが理由です。数学は問題が難しいことが多く、完答が狙いにくいためオススメしないです。
ただ、どの科目も大学入試と比較して範囲が狭く、数カ月程度で範囲を一周できることが殆どです。自身の志望する研究室の分野と合わせて科目をセレクトすると良いです。
情報系科目
上に行くほどオススメ
- 論理回路(オススメ)
- アルゴリズム論(オススメ)
- 計算機学
- オートマトン
- 情報論理学
- 応用数学(フーリエ変換、複素関数、ラプラス変換)
- 一般教養の数学(線形代数、微分積分)
論理回路、アルゴリズム論を特にオススメします。早いうちから勉強し、身に付きやすいため即戦力になりやすいです。範囲もあまり広くないことから、志望する大学院の出題科目に入っている際は、選択科目に検討する価値ありです。
計算機学は、知識問題が出題される場合もあります。大学毎に癖がありますので、ピンポイントの対策が難しいのでこの順位です。
それ以下は、特別難しいことは無いですがマニアックな科目になります。対策のしづらさから下位に位置付けています。
最後に
院試のための勉強も重要ですが、大学によってはGPA(内申)を重視される場合があります。志望する大学院の教授の方にコンタクトを取り、考慮の度合いを質問しておくと吉です。