ショットキー接合、オーミック接合とは
金属と半導体接合時に見られる現象です。両者の持つ仕事関数の大小関係により、整流性を示すか、オーム抵抗のように働くか決まります。
バンド図の大小関係により、この現象を説明することができます。
前提知識
金属や、半導体のフェルミ準位にある電子を真空中に取り出すために必要なエネルギーを仕事関数と言います。金属の仕事関数を\(\phi _{m}\)、半導体の仕事関数を\(\phi _{s}\)とします。
また、半導体の伝導帯の底にある電子を真空中に取り出すために必要なエネルギーを電子親和力と言います。\(\chi_{s}\)で表します。
金属と半導体を接触する前は、以下のバンド図になります。

金属-n型半導体接合のバンド図、振る舞い
前提知識の説明により、金属、半導体の仕事関数\(\phi _{m}\)、\(\phi _{s}\)の大小関係が振る舞いに影響します。
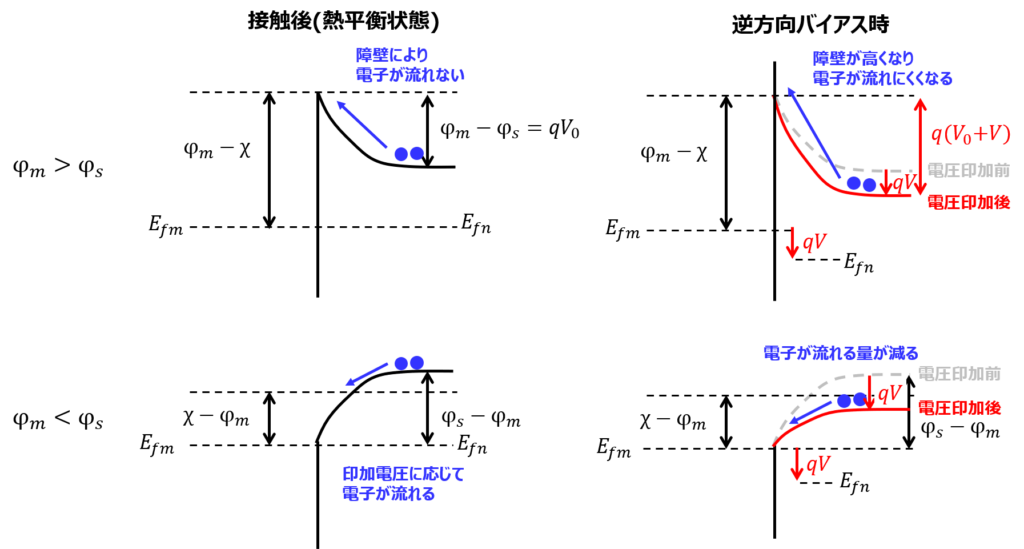
\(\phi _{m}>\phi _{s}\)のとき (ショットキー接合)
半導体側のフェルミ準位\(E_{fs}\)は、金属側の\(E_{fm}\)よりも高いです。
よって、電子が金属側へ移動し、電場が発生します。その結果、拡散電位が形成されます。
この結果、下記のようなバンド図になります。
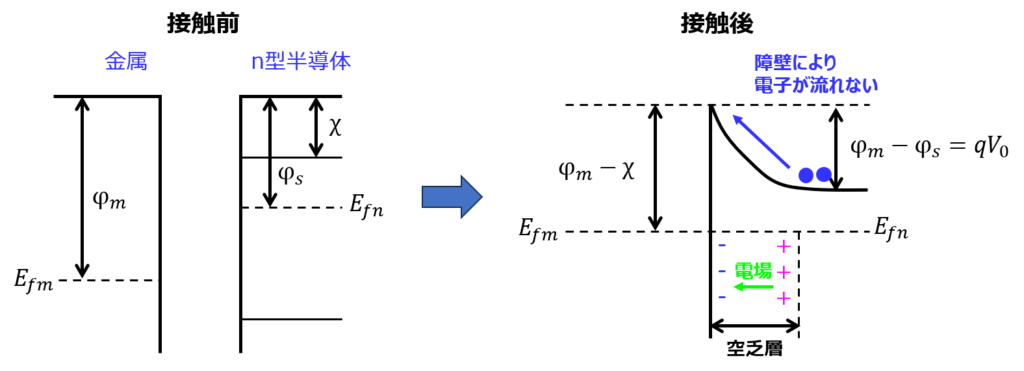
障壁\(qV_{0}=\phi _{m}-\phi _{s}\)により、小さな電圧をかけても電流は流れません。(整流性)
これを、ショットキー接合と言います。
\(\phi _{m}<\phi _{s}\)のとき (オーミック接合)
ショットキー接合とは逆に、金属側のフェルミ準位の方が半導体側よりも高くなります。
ですので、金属側の電子が半導体側へ移動し、拡散電位が形成されます。
この結果、下記のようなバンド図になります。
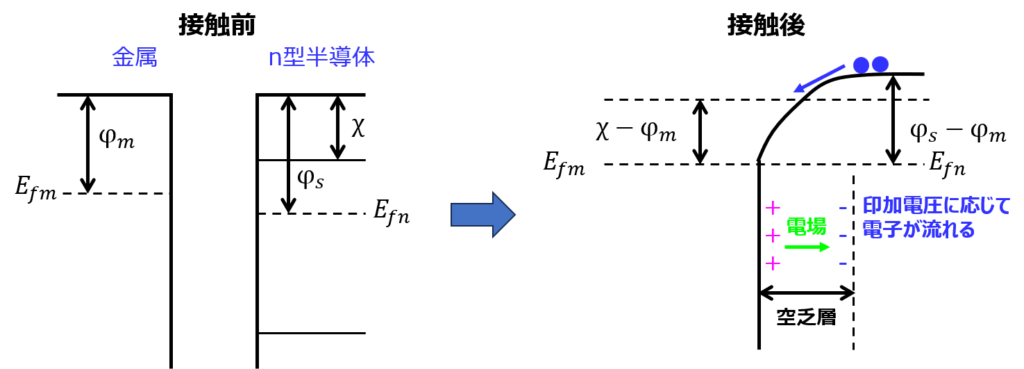
半導体側の伝導帯の準位が金属側に対し高いため、順方向電圧をかけると、その量に応じて電子が流れます。(オーミック接合と言います。)
電圧印加時の振る舞い
前節の説明をバンド図を使用して掘り下げていきます。印加する電圧の方向次第で、電流の流れ方が変わります。
順方向バイアス時 (金属側に正の電圧)
金属側の準位が下がり、障壁高さが低くなります。\(qV_{0}⇒q(V_{0}-V)\)
この結果、半導体側から電子が流れやすくなります。
ショットキー接合時は、ある電圧以上になると、障壁高さが無視できるようになり、電子が流れるようになります。
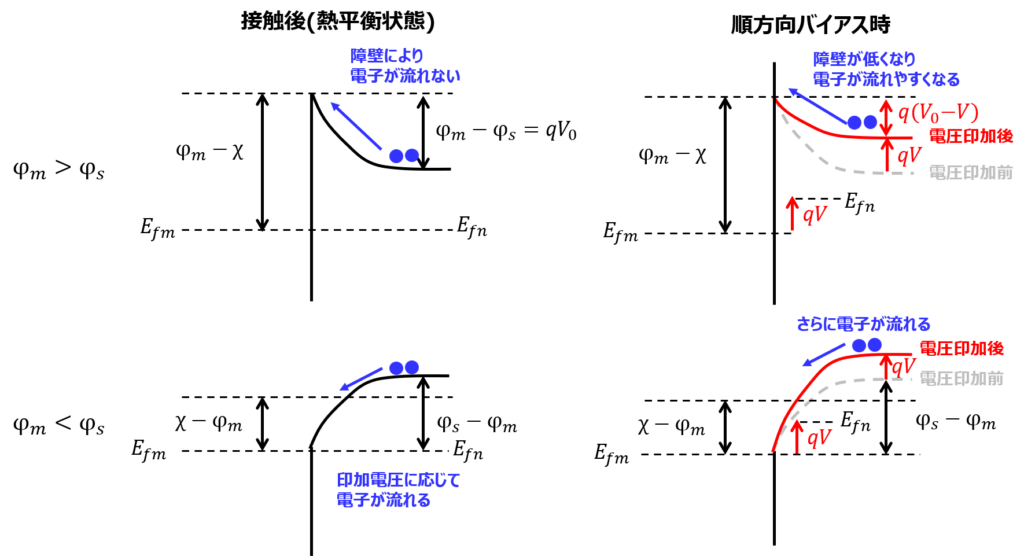
逆方向バイアス時(金属側に負の電圧)
順方向バイアス時と逆の振る舞いになります。障壁高さが高くなり、殆ど電流が流れなくなります。
空乏層の解析
空乏層の長さ\(x_{n}\)は、以前の記事で説明したポアソンの式を利用し、下記の式で表せます。
\begin{aligned}\dfrac{d^{2}V}{dx^{2}}=-\dfrac{qN_{D}}{q}\\ V=qN_{D}\left( x_{n}x-\dfrac{x^{2}}{2}\right) \\ x_{n}=\sqrt{\dfrac{2\varepsilon (V_{0}-V)}{qN_{D}}}\end{aligned}
なお、\(\varepsilon\)は半導体の誘電率。\(N_{D}\)はドナー濃度です。\(V\)は印加した電圧を示しており、順方向が正です。
このとき、空乏層内の単位面積当たりの空間電荷量は以下で表せます。
\begin{eqnarray}Q=qN_{D}x_{n}=\sqrt{2\varepsilon qN_{D}\left( V_{0}-V\right) }\end{eqnarray}
これを用い、単位長さあたりの静電容量は以下で表せます。
\begin{eqnarray}C=-\dfrac{dQ}{dV}=\sqrt{\dfrac{\varepsilon qN_{D}}{2\left( V_{0}-V\right) }}\end{eqnarray}
順方向電圧が印加するほど\(\dfrac{1}{C^{2}\)は小さくなる ⇒ 静電容量が大きくなることが分かりました。(電荷量が小さくなり、空乏層幅が狭くなるため)
金属-p型半導体接合のバンド図、振る舞い
n型半導体と振る舞いが逆になります。
金属から半導体側へ電子が流れるため、電場の向きがn型と逆になります。その結果、仕事関数の大小関係により動作を考えていきます。
\(\phi _{m}>\phi _{s}\)のとき (オーミック接合)
上記の説明により、下記のバンド図になります。p型半導体の場合、価電子帯のエネルギーバンドに注目します。

価電子帯の頂点の準位が、金属側に対し低いことが分かります。このため、正孔は印加した電圧に応じて金属へ流れます。
n型半導体ではショットキー接合だったが、p型半導体の場合はオーミック接合になることが分かりました。
\(\phi _{m}<\phi _{s}\)のとき (ショットキー接合)
こちらも同様の考え方をします。
n型半導体の場合は、伝導帯の底の準位が金属側対し高かったです。
これにより、価電子帯の頂点の準位も、金属側の準位に対し高くなります。
よって、正孔から見ると障壁が発生し、金属に流れないことが分かります。

印可電圧を大きくすると、正孔が流れるようになります。ショットキー接合であることが分かりました。
電圧印加時の振る舞い
p型半導体の場合、金属側に負の電圧をかける逆方向バイアスにすることで、正孔が流れます。
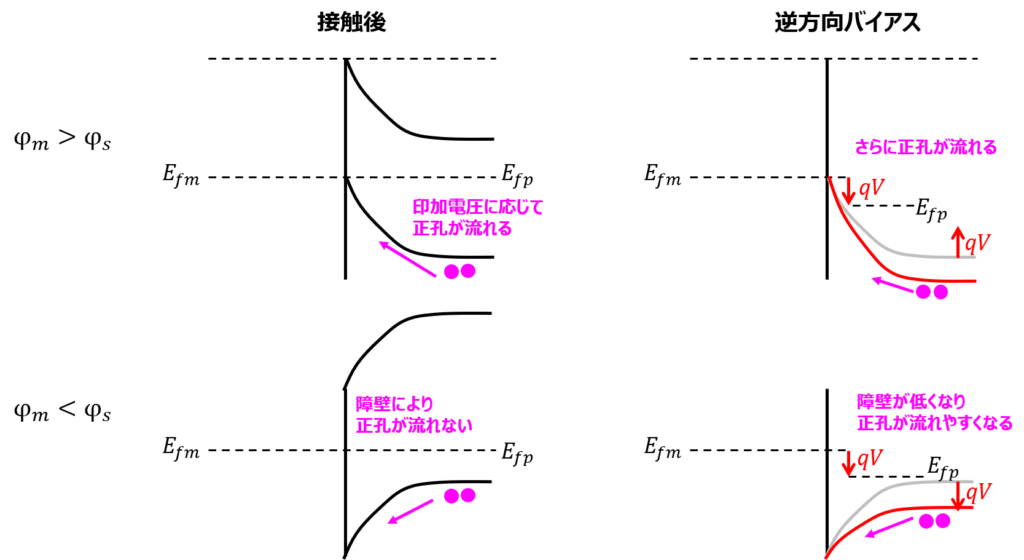
逆に、順方向バイアスの場合は、正孔が流れにくくなります。

最後に
以前の記事では、MOSトランジスタの動作原理、バンド図を説明しました。(院試頻出分野)
仕事関数の大小関係により、バンド図を記載し、動作を説明する一連の流れは、半導体デバイスの院試頻出です。何度も練習し、是非自分のものにしてください。
参考文献
半導体工学 基礎からデバイスまで 第2版:東京電機大学出版 P80-93