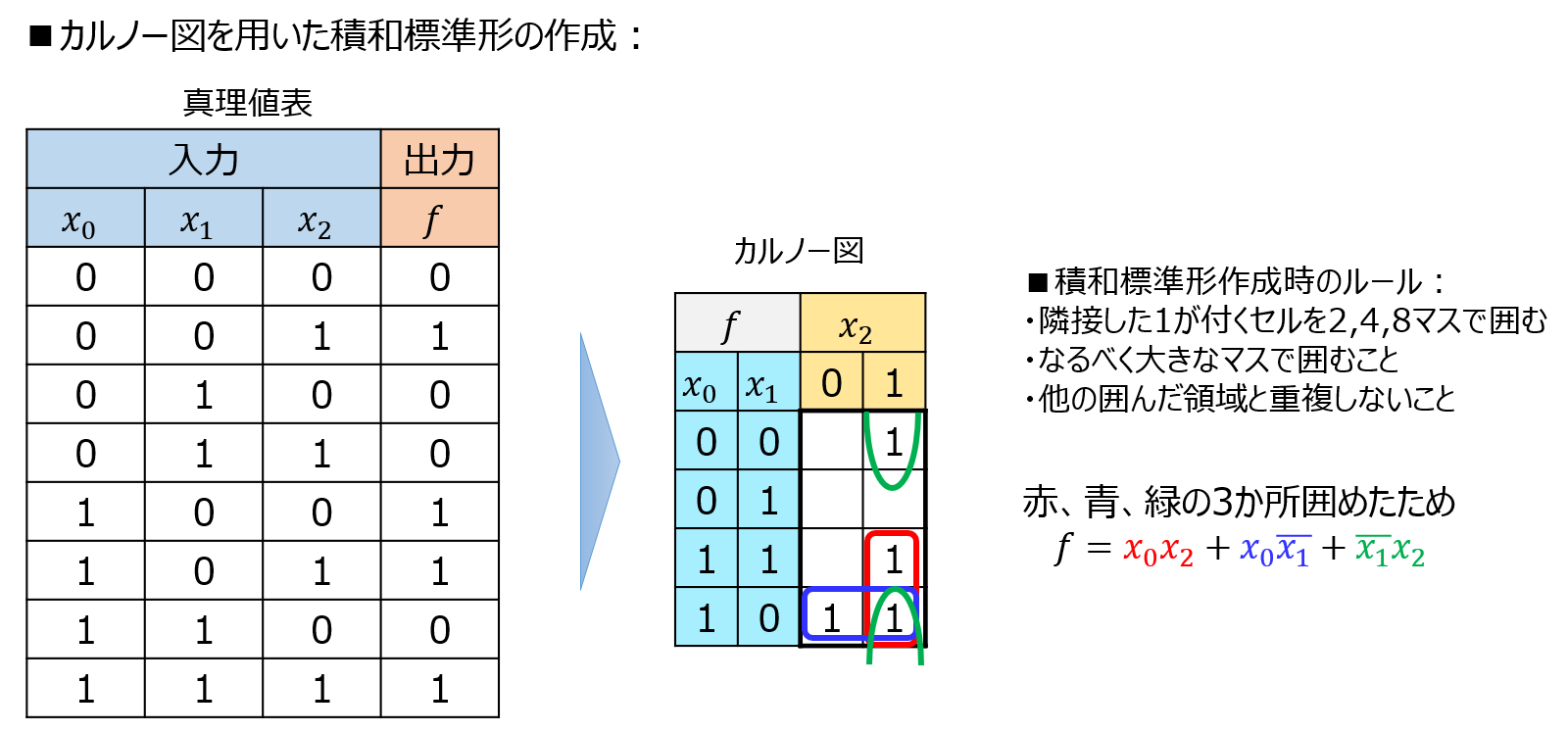
以下の真理値表で表される論理関数の積和標準形、和積標準形を求めよ。
真理値表:
| \(x_{0}\) | \(x_{1}\) | \(x_{2}\) | \(f(x_{0},x_{1},x_{2})\) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
はじめに
論理関数の説明を最初に行い、積和形、和積形との関係を説明していきます。
論理関数とは
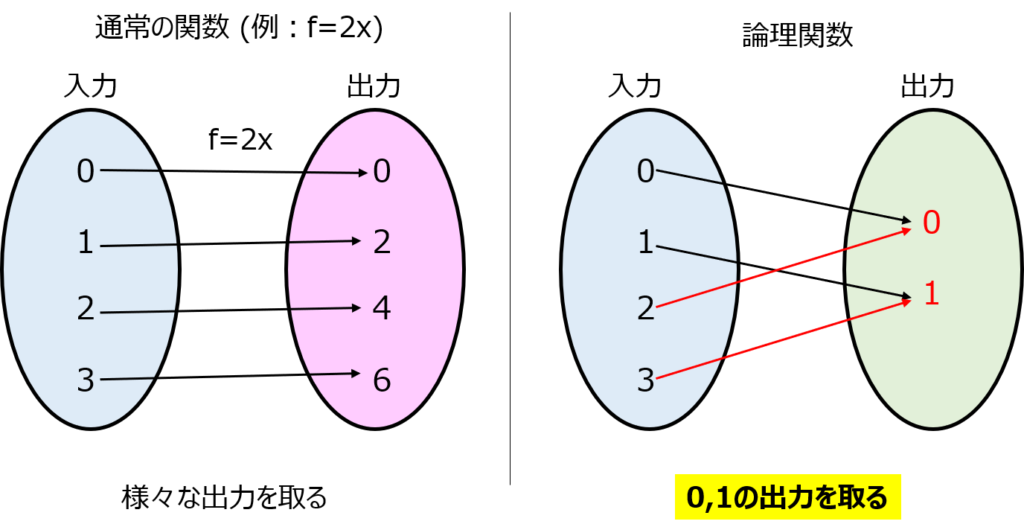
0,1の離散的な2通りの入力に対し、0,1の2通りを出力として返す機能を言います。
中学数学で、y=2xなる概念が出てきたと思います。xを代入すると、2倍した値を出力として返す機能を指しています。
上記の関数は連続的な値に対して、0,1以外の値でも出力を返します。
しかし、論理関数の場合は、計算機での処理を想定しているため、0,1の2通りしかありません。
入力変数に対し出力を返す流れは変わらないものの、入出力の中身が異なることがキーポイントです。
積和系とは
論理関数\(f(x_{0},x_{1},x_{2}, \cdots, x_{n})\)について
\begin{aligned}f(x_{0},x_{1},x_{2}, \cdots, x_{n})=x_{0}x_{1}+x_{1}x_{2}+x_{n-1}x_{n}\end{aligned}など、積項の和として表示したものを言います。
特に、\(x_{1}x_{2}+x_{1}\overline{x_{2}}=x_{1}(x_{2}+\overline{x_{2}})=x_{1}\)などを用いて、マージできる項をくっつけ、(1)式を限界まで簡単化したものを積和標準形(最簡形)と言います。
限界まで簡単化することにより、論理回路を組む際に必要な素子を低減することが出来ます。
和積系とは
積和系とは逆です。
\begin{aligned}f(x_{0},x_{1},x_{2}, \cdots, x_{n})=(x_{0}+x_{1})(x_{1}+x_{2})(x_{n-1}+x_{n})\end{aligned}など、論理関数を和項の積として表示したものを言います。
特に、和項を最大限用いて(2)式を表したものを和積標準形と言います。
標準形の求め方
積和標準形の求め方
カルノー図を用いる方法
院試では、この方法を用いることが多いです。
n変数ならば、\(2^{n}\)のマスを用意し、出力1を返す入力の組み合わせのマスに1を入れます。
1が隣接するマスを2の倍数ずつ囲み、囲んだマスで変数が変化しないものを項として抽出します。
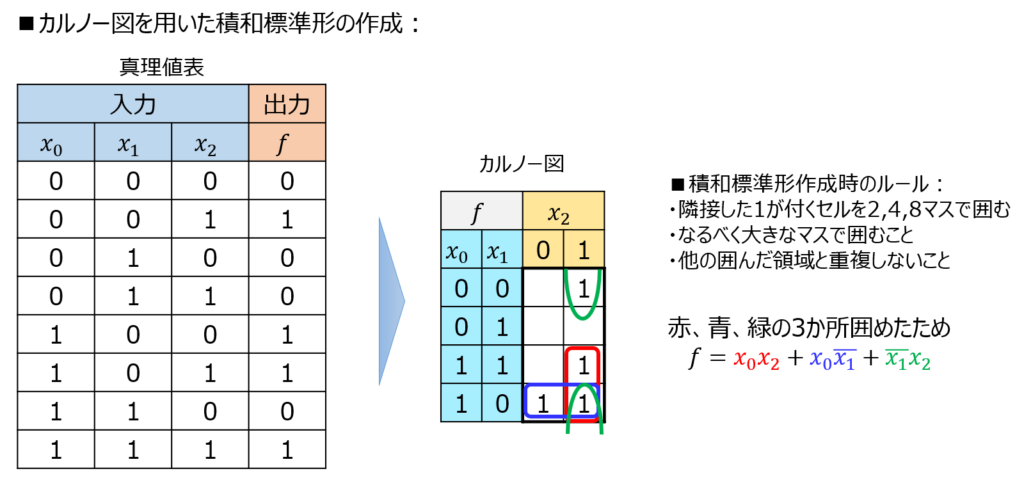
注意点としては、上から順に入力変数の組み合わせが(00,01,“11”,10)になる順にマスを作っていくことです。
これは、2つの入力変数を片方ずつ変えなければいけないルールに基づいた記載になっています。
丸を囲む意味として、\(x_{1}x_{2}=(1,1)(1,0)\)を満たす項\(x_{1}x_{2}+x_{1}\overline{x_{2}}=x_{1}(x_{2}+\overline{x_{2}})=x_{1}\)
のように、補元律\(x_{1}+\overline{x_{1}}=1\)を取ることに対応しています。これを繰り返すことで式を簡単化できます。
クワイン・マクラスキー法を用いる方法
こちらの記事で詳細解説しています。本記事では割愛します。
和積標準形の求め方
こちらは、真理値表からすぐに求めることができます。
ただ、入力を反転させたりと、気を付けないといけない部分があります。
- 出力0を返す入力の組み合わせに印を付ける
- それぞれの入力の組み合わせに対し、0,1を反転した和項を掛け合わせる。
<図解例>
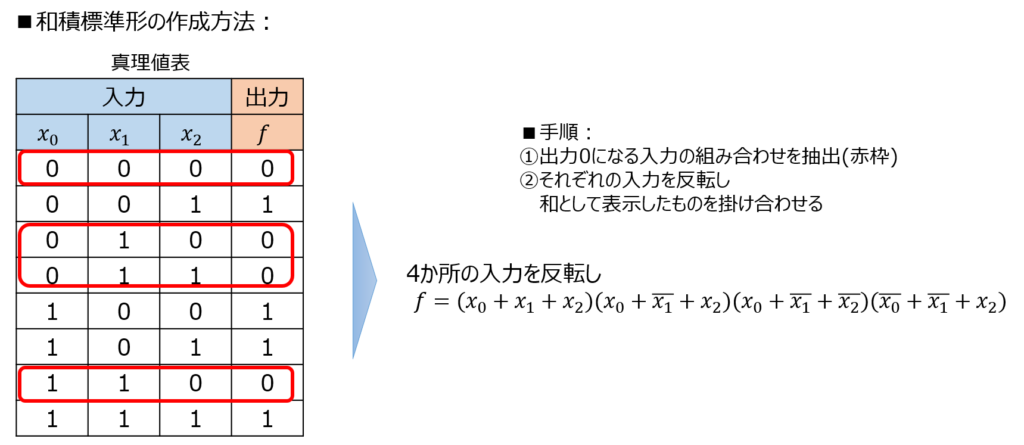
わざわざ出力0になる入力を選ぶ理由は、ドモルガン律を利用するからです。
出力0になる組み合わせを真理値表を読み取り、論理関数が下記で表されたとします。\begin{aligned}\overline{f}=x_{0}x_{1}+x_{1}x_{2}\end{aligned}
出力0を与える入力を考えるので、左辺が反転しています。
これにNOTを取ると、ドモルガン律を利用して
\begin{aligned}\overline{\overline{f}} &= \overline{x_{0}x_{1}+x_{1}x_{2}} \\ f&=(\overline{x_{0}x_{1}})(\overline{x_{1}x_{2}}) \\ &=(\overline{x_{0}}+\overline{x_{1}})(\overline{x_{1}}+\overline{x_{2}}) \end{aligned}
のように、出力1を返す論理式を和積系で表現することができました。
このように、出力を反転させることを前提にしているので、出力が0になる組み合わせを選ぶということですね。
解答例
積和標準形
与えられた論理関数をカルノー図として表すと下記のようになる。
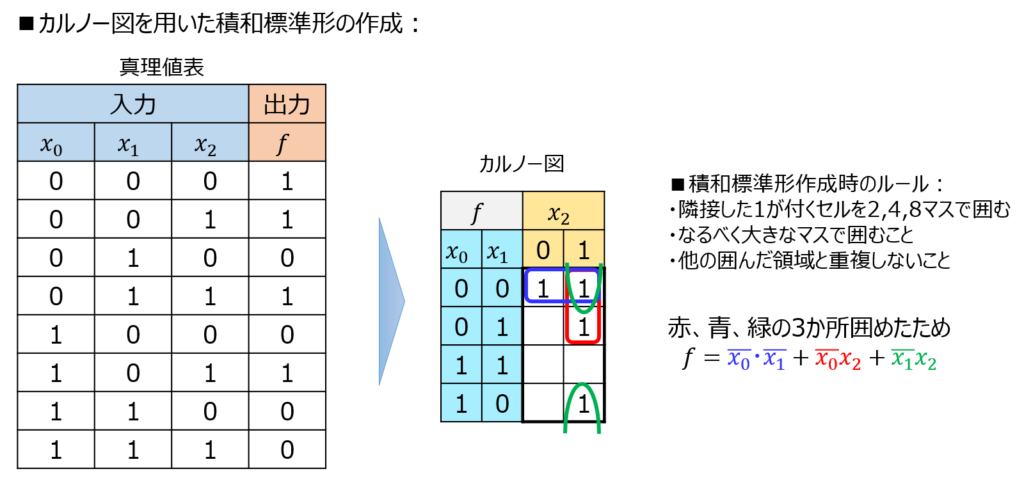
\((x_{0},x_{1},x_{2})=(0,0,0)と(0,0,1)、(0,0,1)と(0,1,1)、(0,0,1)と(1,0,1)\)の3つが隣接しているので、
\begin{aligned}f(x_{0},x_{1},x_{2})=\overline{x_{0}}\overline{x_{1}}+\overline{x_{0}}x_{2}+\overline{x_{1}}x_{2}\end{aligned}
和積標準形
0になる入力に注目すると、下記のようになる。
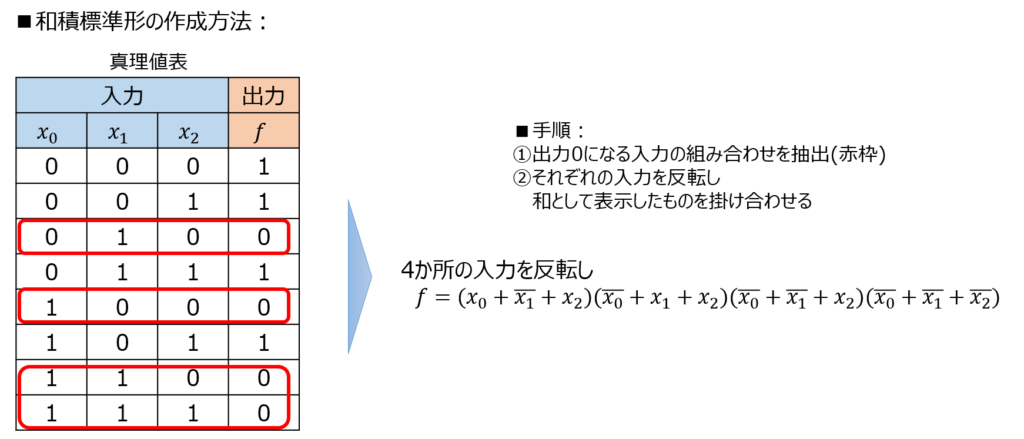
\begin{aligned}f(x_{0},x_{1},x_{2})=(x_{0}+\overline{x_{1}}+x_{2})(\overline{x_{0}}+x_{1}+x_{2})(\overline{x_{0}}+\overline{x_{1}}+x_{2})(\overline{x_{0}}+\overline{x_{1}}+\overline{x_{2}})\end{aligned}
最後に
本問は、東北大の院試でよく出題されます。
序盤の問題で出てくることが多いので、必ず得点できるようになりましょう。