鏡像法とは？点電荷における典型問題例を解説(院試レベル)

鏡像法とは

ある特定の系において、幾何学的な特徴を利用して特定の位置に仮想的に電荷を置けば、手計算で電場分布を求められるようになる方法を言います。

本記事では、院試でよく問われる代表的な3つの系における鏡像電荷の置き方及び電場分布の求め方、各種特性を紹介します。

平行平板における電場分布

下記のように、接地した導体平板に正対している電荷+qが(x,y,z)=(a,0,0)に存在する系の電場分布を考えます。(ただしa>0)

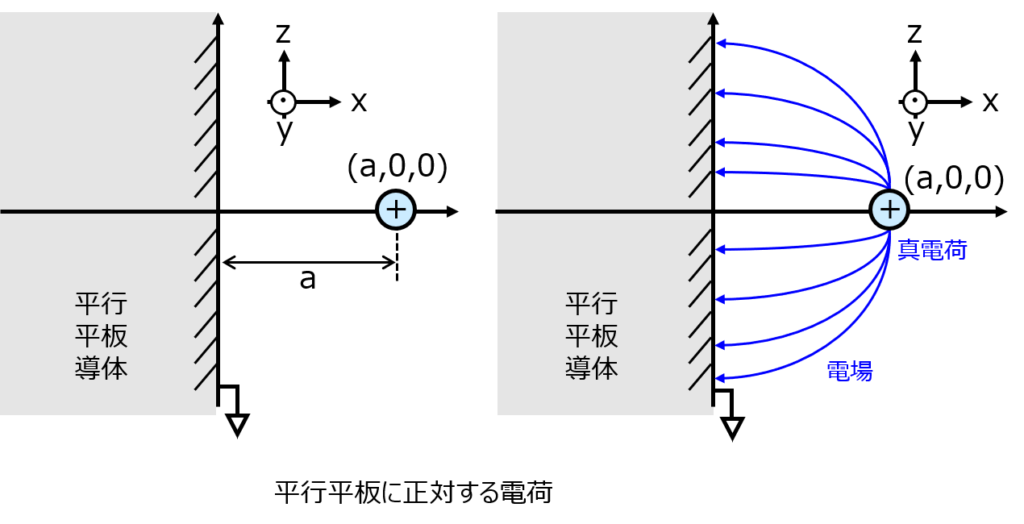
導体内部で電場は発生しないので、境界条件により、平板に対し垂直に電場がかかります。となると、平板表面に電荷が誘起されます。

(x,y,z)平面上の任意の点における電場を手計算で求めようとすると、平面板で無限に誘起されている電荷から発生する電場を考慮に入れなければならず、手計算で求めるには難しい(積分できない)です。

ここで出てくるのが鏡像法の考え方です。

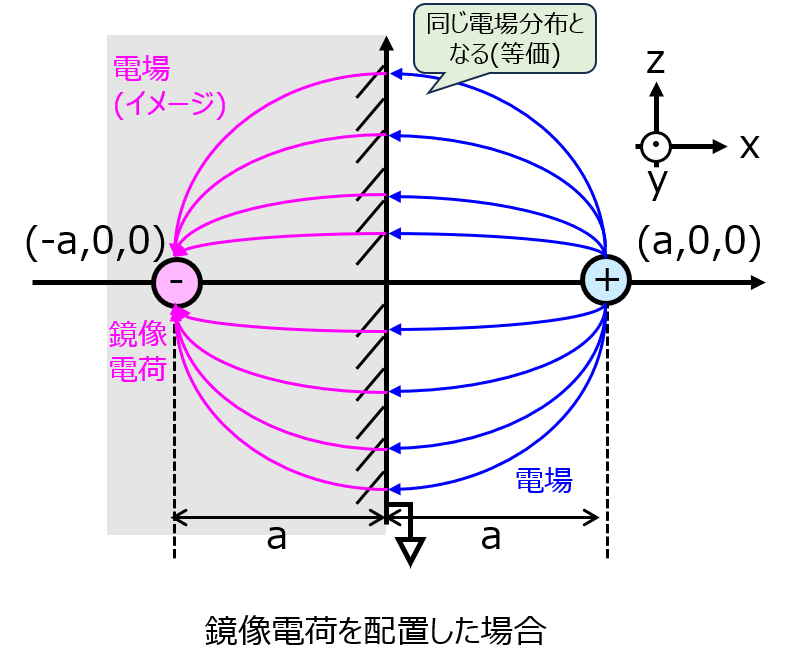
平行平板に対し対称な点(-a,0,0)に鏡像電荷(-q)を置きます。(平行平板は取り払う。)
この場合でも、平行平板の存在する(0,y,z)における電場が垂直になることが幾何学的に分かります。よって、元の系と同等であると言えます。

これより、平行平板からx=a離れた地点に点電荷+qを置いた系における電場分布の計算は、x=-aに点電荷-qを仮想的に置いた場合で考えて良いことになります。

※鏡像電荷の置き方が正しいかどうかは、導体平板上の電位がV=0になるかどうかで判断すれば良いです。ただ、これを試験中にやっているとキリが無いので、パターンとして覚えておくことを推奨します。

電場分布の求め方

全体方針

点電荷における電位の式を用います。

\begin{aligned}V=\dfrac{q}{4 \pi \varepsilon_{o}r}\end{aligned}

\begin{aligned}\boldsymbol{E}=- grad V\end{aligned}の関係式で勾配を取ってやれば、電場を数学的に求められることが分かります。

電位の計算

(1)式より、2つの点電荷を合わせた任意の点(x,y,z)の電位は

\begin{aligned}V(x,y,z)=\dfrac{1}{4 \pi \varepsilon_{o}}=\left \lbrace \dfrac{q}{\sqrt{(x-a)^{2}+y^{2}+z^{2}}}-\dfrac{q}{\sqrt{(x+a)^{2}+y^{2}+z^{2}}} \right \rbrace \end{aligned}

電場の計算

これを(2)式を用いて微分する。まず、x成分$E_{x}$は

\begin{aligned}E_{x}=-\dfrac{1}{4 \pi \varepsilon_{o}}\left \lbrace – \dfrac{q(x-a)}{((x-a)^{2}+y^{2}+z^{2})^{3/2}} + \dfrac{q(x+a)}{((x+a)^{2}+y^{2}+z^{2})^{3/2}} \right \rbrace \end{aligned}

次に、y成分$E_{y}$とz成分$E_{z}$は、同様にして

\begin{aligned}E_{y}=-\dfrac{1}{4 \pi \varepsilon_{o}}\left \lbrace – \dfrac{qy}{((x-a)^{2}+y^{2}+z^{2})^{3/2}} + \dfrac{qy}{((x+a)^{2}+y^{2}+z^{2})^{3/2}} \right \rbrace \\ E_{z}=-\dfrac{1}{4 \pi \varepsilon_{o}}\left \lbrace – \dfrac{qz}{((x-a)^{2}+y^{2}+z^{2})^{3/2}} + \dfrac{qz}{((x+a)^{2}+y^{2}+z^{2})^{3/2}} \right \rbrace \end{aligned}

以上で、基本的なパラメータを求められましたが、院試では追加で問われる事項があります。下記では、その説明をしていきます。

平行平板に誘起される電荷の総量

平行平板のある点(0,y,z)における面電荷密度$\sigma$を積分することで求めます。ある点における面電荷密度は、電場の式を用いて

\begin{aligned}\sigma=\varepsilon_{o}E\end{aligned}

と表されますから、

\begin{aligned}\sigma&=-\dfrac{aq}{2 \pi}\dfrac{1}{a^{2}+y^{2}+z^{2}} \\ &=-\dfrac{aq}{2 \pi r^{3}}\end{aligned}

と置けます。これを、平板の中心から半径$s=\sqrt{y^{2}+z^{2}}$離れた微小円環で誘起される微小電荷$dq$は

\begin{aligned}dq&=\sigma ･ 2 \pi s･ds \\ &=-\dfrac{aqs}{(a^{2}+s^{2})^{3/2}}ds\end{aligned}

半径sを0~∞の範囲で積分すると、平板全体に誘起される電荷の総量Qが求められ

\begin{aligned}Q&=-\int^{\infty}_{0} \dfrac{aqs}{(a^{2}+s^{2})^{3/2}}ds \\ &=aq \left \lbrack \dfrac{1}{\sqrt{a^{2}+s^{2}}} \right \rbrack ^{\infty}_{0} \\ &= -q\end{aligned}

であり、鏡像電荷と等しいことが分かりました。

平行平板と点電荷の間の引力

鏡像電荷を置いた場合と等価ですから、クーロンの法則により

\begin{aligned}F&=\dfrac{1}{4 \pi \varepsilon_{o}}\dfrac{q*(-q)}{(2a)^{2}} \\ &=-\dfrac{q^{2}}{16 \pi \varepsilon_{o}a^{2}}\end{aligned}

接地した導体球における電場分布

このケースもよく問われます。結論、球の中心から$h=\frac{a^{2}}{d}$離れた地点に$q’=-\frac{a}{d}q$の鏡像電荷を置くことで等価な電位分布になります。

この場合も電場分布も、平行平板のときと同じ手順で求めることができます。

鏡像電荷の設置場所の理由

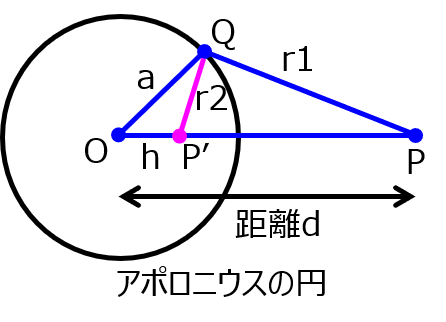
中学数学で利用した相似の知識を利用すれば、上記の理由が分かります。

△OP’Qと△OPQが相似になるので、$\dfrac{h}{a}=\dfrac{a}{d}$。

これを解いて、$h=\dfrac{a^{2}}{d}$

点Qにおける電位は、クーロンの法則より、\begin{aligned}V=\dfrac{1}{4 \pi \varepsilon_{o}}\left( \dfrac{q}{r_{1}}+\dfrac{q’}{r_{2}} \right) \end{aligned}

で表される。($r_{1},r_{2}$は、点電荷、鏡像電荷から点Qまでの距離)

接地：$V=0$の条件の元、上式を代入すれば、$-\dfrac{aq}{d}$を得る。

電場分布の計算方法

電位の計算

余弦定理と(1)式を用いて、下記のようになります。

\begin{aligned}V=\dfrac{q}{4 \pi \varepsilon_{o}}\left( \dfrac{1}{\sqrt{r^{2}+d^{2}-2rd\cos \theta}}-\dfrac{a}{d\sqrt{r^{2}+d^{2}-2rh\cos \theta}}\right)\end{aligned}

電場の計算

系方向成分$r$と周方向成分$\theta$で偏微分することで、それぞれの電場成分が求まります。

\begin{cases} E_{r}=\dfrac{\partial{V}}{\partial{r}} \\ E_{\theta}=\dfrac{1}{r}\dfrac{\partial{V}}{\partial{\theta}}\end{cases}

\begin{cases}E_{r}=\dfrac{q}{4 \pi \varepsilon_{o}}\left( \dfrac{d\cos\theta-r}{(r^{2}+d^{2}-2rd\cos \theta)^{3/2}} -\dfrac{a(h\cos\theta-r)}{d(r^{2}+h^{2}-2rh\cos \theta)^{3/2}} \right) \\ E_{\theta}=\dfrac{q}{4 \pi \varepsilon_{o}}\left(-\dfrac{h \sin \theta }{(r^{2}+h^{2}-2hr \cos \theta )^{3/2}}+\dfrac{h \sin \theta }{(r^{2}+h^{2}-2hr \cos \theta)^{3/2}} \right) \end{cases}

となります。

導体球に誘起される電荷の総量

前節で求めた電場成分$E_{r}$に対し、$r=a$を考えると、面電荷密度は$\sigma=\varepsilon_{o}E_{r}$と置けるので

\begin{aligned}\sigma=-\dfrac{q}{4 \pi a}\dfrac{(d^{2}-a^{2})}{(a^{2}+d^{2}-2ad\cos \theta)^{3/2}}\end{aligned}

$\theta$から$\theta+d\theta$で囲まれる微小円環における電荷密度$dq’$は

\begin{aligned}dq’&=\sigma 2 \pi a^{2}\sin \theta d\theta \\ &=-\dfrac{qa}{2}(d^{2}-a^{2})\dfrac{\sin \theta}{(a^{2}+d^{2}-2ad \cos \theta)^{3/2}}d \theta \end{aligned}

$\theta$を0~πの間で積分することで、求める誘導電荷は

\begin{aligned}q’&=\dfrac{qa}{2}(d^{2}-a^{2})\int^{\pi}_{0} \dfrac{\sin \theta}{(a^{2}+d^{2}-2ad \cos \theta)^{3/2}}d \theta \\ &=-q \dfrac{a}{d}\end{aligned}

このように、鏡像電荷と等しいことが分かりました。点電荷qより電荷量が小さいため、このような静電誘導を不完全誘導と言います。

導体球と点電荷の間の引力

前節と同じく、鏡像電荷と真電荷の間の力を求めれば良いです。クーロンの法則により

\begin{aligned}F&=\dfrac{q^{2}}{4 \pi \varepsilon_{o}}\dfrac{ad}{(d^{2}-a^{2})^{2}}\end{aligned}

真電荷を一定速度vで導体球に向けて移動させたとき、導体球に流れる電流

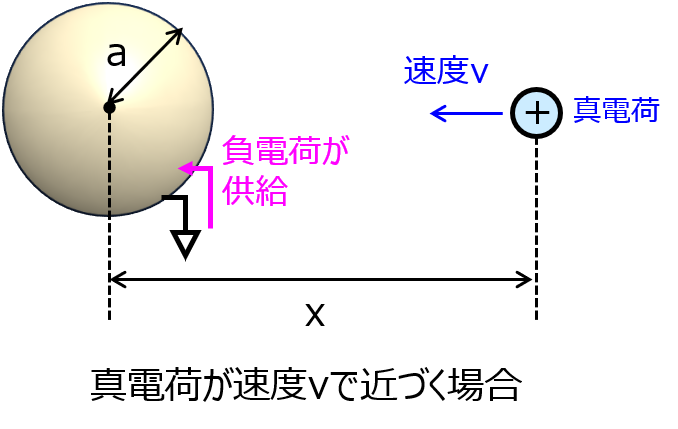
これも院試でよく出てきます。この機会に是非覚えましょう。

電流$I$は電荷$Q$の時間微分に等しいことを利用することがヒントです。導体球に近づくほど、誘起される電荷(負)の量が大きくなるため、符号に注意し

\begin{aligned}I=-\dfrac{dQ}{dt}\end{aligned}

前節より、真電荷が導体球の中心から$x$離れているときに導体球に誘起される電荷は$q’=\dfrac{a}{x}q$

これを時間微分することで、導体球に流れる電流は

\begin{aligned}I&=-\dfrac{dq’}{dt} \\ &=\dfrac{d}{dt}\left(\dfrac{aq}{x}\right) \\ &=-\dfrac{dx}{dt}\dfrac{d}{dx} \left(\dfrac{aq}{x}\right) \\ &=\dfrac{aqv}{x^{2}}\end{aligned}

ただし、$-v=\dfrac{dx}{dt}$です。

直角に折り曲げた導体板における電場分布

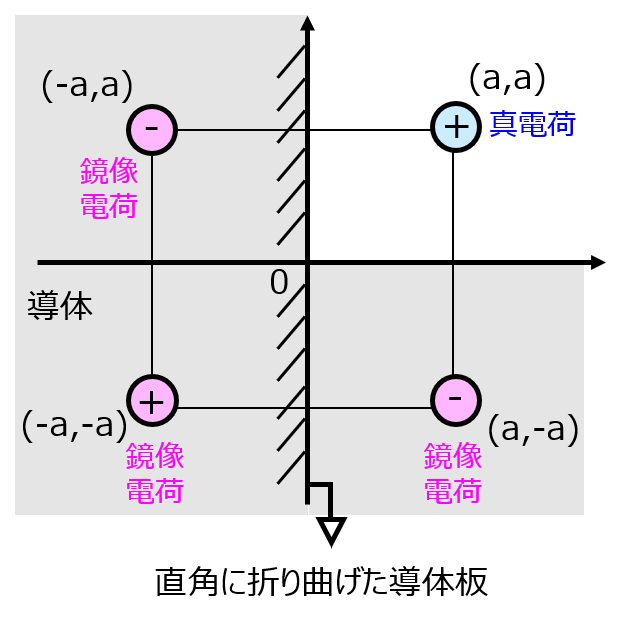
本ケースは計算が非常に難しいですが、実際に九大の院試で出題されたことがあります。鏡像法に関する問題の中で最難だと思います。

出題されるからには得点する必要があるため、本サイトでも取り上げます。自力でできるようになれば、鏡像法に関しては怖いもの無しでしょう。

電荷分布

まずは、鏡像電荷の配置について考えます。平行平板1枚の場合は、正対した箇所に同じ電荷量を持つ負の鏡像電荷を設置すれば良かったですが、今回は折れ曲がっています。

よって、それぞれの平板に対し正対した箇所に2つの鏡像電荷を置きます。

ですが、これだけで十分なのでしょうか？実際は、真電荷とそれぞれの平板間に対する電場の相互作用は実現できていますが、平板同士の相互作用は加味できていません。

そこで、真電荷の対角線上にも鏡像電荷+qを置きます。先ほど置いた-qの鏡像電荷に対する鏡像電荷をさらに設定したことから、これで抜けていた相互作用を実現できます。この電場分布で平板表面の電位を計算すれば全て同じ電位(等電位面)になります。(各自で計算をお願いします。)

電位分布

先ほどの2通りの場合と同様に、まずは電位を考えます。

式(1)の重ね合わせで実現するので

$$\begin{eqnarray}V = \dfrac{q}{4 \pi \varepsilon_{o}}& &\left ( \dfrac{1}{\sqrt{(x-a)^{2}+(y-a)^{2}+z^{2}}} \right. \\ & & \left. – \dfrac{1}{\sqrt{(x-a)^{2}+(y+a)^{2}+z^{2}}} \right. \\ & & \left. – \dfrac{1}{\sqrt{(x+a)^{2}+(y-a)^{2}+z^{2}}} \right. \\ & & \left. + \dfrac{1}{\sqrt{(x+a)^{2}+(y+a)^{2}+z^{2}}} \right) \end{eqnarray}$$

電場分布

これは本当に計算が大変なので、$x=0$にあるy方向に無限に伸びる平板の電位分布を代表的にやります。$y=0$にある平板に対しては、x,yを逆にすることで求められます。

x方向の電場成分を考えて

\begin{aligned}E_{x}=-\dfrac{q}{2 \pi \varepsilon_{o} }\left( \dfrac{a}{(x^{2}+(y-a)^{2}+z^{2})^{3/2}} – \dfrac{a}{(x^{2}+(y+a)^{2}+z^{2})^{3/2}}\right)\end{aligned}

導体平板に誘起される全電荷

$x=0$の平板で発生する全電荷$Q_{1}$と、$y=0$の境界で発生する全電荷$Q_{2}$を足し合わせた電荷が全電荷に相当します。

まず、電荷$Q_{1}$について、面電荷密度$\sigma_{1}=\varepsilon_{o}E_{x}$は

\begin{aligned}\sigma_{1}=-\dfrac{q}{2 \pi}\left( \dfrac{a}{(x^{2}+(y-a)^{2}+z^{2})^{3/2}} – \dfrac{a}{(x^{2}+(y+a)^{2}+z^{2})^{3/2}}\right)\end{aligned}

これをyz平面 (z>0)の範囲で積分して

\begin{aligned}Q_{1}&=\int^{\infty}_{-\infty}\int^{\infty}_{0}\sigma_{1}dydz \\ &=-\dfrac{q}{2 \pi}\left( \dfrac{a}{(x^{2}+(y-a)^{2}+z^{2})^{3/2}} – \dfrac{a}{(x^{2}+(y+a)^{2}+z^{2})^{3/2}}\right)dydz \\ &= -\dfrac{qa}{\pi}\int^{\infty}_{0}\left(\dfrac{1}{a^{2}+(y-a)^{2}}-\dfrac{1}{a^{2}+(y+a)^{2}}\right)dy \\ &=\dfrac{2q}{\pi}\tan^{-1}\dfrac{a}{a} \\ &=-\dfrac{q}{2}\end{aligned}

このように、2行目の積分結果をtanの逆関数として置くことが、大変重要です。

電荷$Q_{2}$についても、同様にして、xとyを入れ替えればよく

\begin{aligned}Q_{2} &=-\dfrac{q}{2 \pi}\left( \dfrac{a}{(y^{2}+(x-a)^{2}+z^{2})^{3/2}} – \dfrac{a}{(y^{2}+(x+a)^{2}+z^{2})^{3/2}}\right)dydz \\ &= -\dfrac{qa}{\pi}\int^{\infty}_{0}\left(\dfrac{1}{a^{2}+(x-a)^{2}}-\dfrac{1}{a^{2}+(x+a)^{2}}\right)dy \\ &=\dfrac{2q}{\pi}\tan^{-1}\dfrac{a}{a} \\ &=-\dfrac{q}{2}\end{aligned}

よって、導体に誘起される全電荷$Q$は

\begin{aligned}Q&=Q_{1}+Q_{2} \\ &= -\dfrac{q}{2}–\dfrac{q}{2} \\ &= -q\end{aligned}