はじめに
バンド構造は、特定の大学の院試に出ます。特に阪大と九大で出題されます。
本記事では、真性半導体の場合のバンド構造、電子密度を最初に導出し、ベースとなる考え方を示します。そこから、不純物半導体(n型)の場合についても発展項目として考えます。
覚えたいポイントは記載しません。下記の導出過程全て重要なので、理解と暗記を推奨します。
なお、本記事の作成には、阪大の指定教科書及び院試(2020 量子電子物性2)を参考にさせていただきました。お礼を申し上げます。
使用するパラメータの説明
真性半導体
- 伝導帯の有効状態密度:\(N_{c}\)
- 価電子帯の有効状態密度:\(N_{v}\)
- 真性キャリア密度:\(n_{i}\)
- 伝導帯に励起される電子の密度:\(n\)
- 価電子帯の正孔の密度:\(p\)
- 真性フェルミエネルギー:\(E_{i}\)
- フェルミエネルギー:\(E_{f}\)
- 価電子帯上端のエネルギー\(E_{v}\)
- 伝導帯下端のエネルギー\(E_{c}\)
- ボルツマン係数:\(k\)
- 温度:\(T\)
不純物半導体
- アクセプタ密度:\(N_{A}\)
- ドナー密度:\(N_{D}\)
- 正孔を価電子帯へ供給し、イオン化したアクセプタ密度\(N_{A}^{-}\)
- ドナーを伝導帯へ供給し、イオン化したドナー密度:\(N_{D}^{+}\)
- ドナー準位を電子が占有する確率:\(f_{D}(E_{D})\)
真性半導体におけるバンド構造、電子密度
下記のようなエネルギーバンドを考える。(熱平衡状態)

伝導帯の有効状態密度を\(N_{c}\)、価電子帯の有効状態密度を\(N_{v}\)とすると、ある温度で伝導帯に励起される電子の密度\(n\)と正孔の密度\(p\)は、以下のようになる。
\begin{cases}n=N_{c}\exp \left( -\dfrac{E_{c}-E_{f}}{kT}\right) \\ p=N_{v}\exp \left( -\dfrac{E_{f}-E_{v}}{kT}\right) \end{cases}
(\(\exp\)の中の項は、(準位が上のエネルギ) – (準位が下のエネルギー)と覚えましょう。)
真性半導体の場合、下記の式が成立する。
\begin{eqnarray} n_{i}^{2} = np \end{eqnarray}これを、式(1)を代入し
\begin{eqnarray}n_{i}^{2}=np=N_{c}N_{v}\exp \left(-\dfrac{E_{c}-E_{v}}{kT} \right)\end{eqnarray}
バンドギャップは、\(E_{g}=E_{c}-E_{v}\)だから
\begin{eqnarray}n_{i}=\sqrt{N_{c}N_{v}}\exp \left(-\dfrac{E_{g}}{kT} \right)\end{eqnarray}
と表すことができる。
電気的中性条件により、\(p,N_{D}^{+},n,N_{a}^{-}\)には下記の関係がある。
\begin{eqnarray}p+N_{D}^{+}=n+N_{a}^{-}\end{eqnarray}
真性半導体の場合、\(N_{D}^{+}=N_{A}^{-}=0\)なので、\(n=p\)になる。
これを式(1)を代入すると、フェルミエネルギーは次式で示される。
\begin{eqnarray}\exp \left( \dfrac{2E_{f}-E_{c}-E_{n}}{kT}\right) =\dfrac{N_{v}}{N_{c}} \\ E_{f}=\dfrac{E_{c}+E_{v}}{2}+\dfrac{kT}{2}\log \left( \dfrac{N_{v}}{N_{c}}\right)\end{eqnarray}
を得る。
不純物半導体のバンド構造、電子密度
前章までは、どの半導体デバイスの教科書でも記載する内容と思います。一方で、不純物半導体の場合の特性を詳しく立式している教科書は限られてきます。本章では、n型半導体を題材に、伝導帯の電子密度を考えていきます。
温度領域によって変わりますので、結果を見る前に読者の皆様自身で予想下さると理解が深まるかもしれません。
n型不純物半導体の場合、ドナー準位\(E_{d}\)が発生し、伝導帯へドナーが励起しやすくなります。下記(左)のようなバンド図になります。
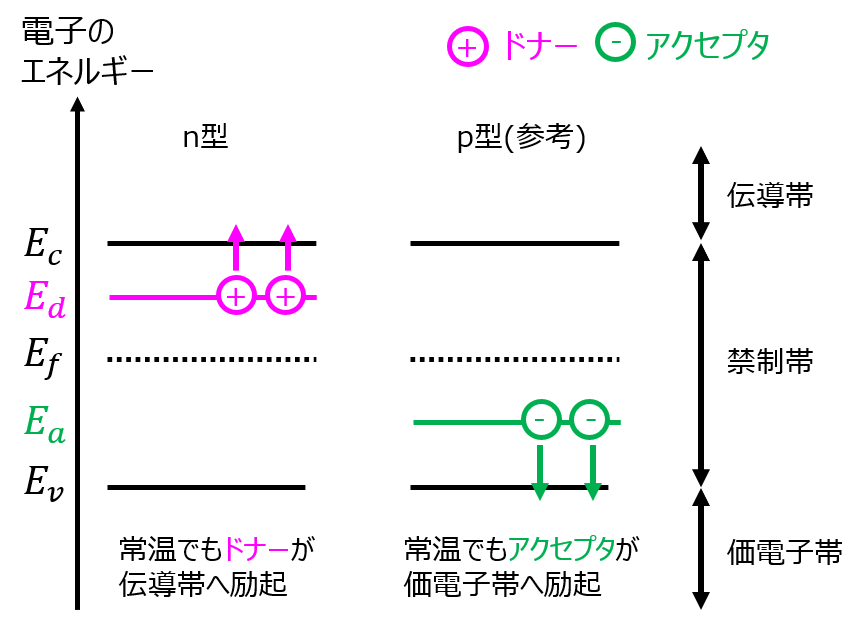
ドナーを伝導帯へ供給し、イオン化したドナー密度\(N_{D}^{+}\)を、分布関数を用いると、下記式で表すことができる。
\begin{eqnarray}N_{D}^{+}=N_{D}-N_{D}f_{D}(E_{D})\end{eqnarray}
n型半導体のため、アクセプタイオンの影響は無視し
\begin{eqnarray}N_{A}^{-}=0\end{eqnarray}
式(8)(9)を式(5)に代入すると、下記のようになる。
\begin{eqnarray}n=p+N_{D}^{+}\end{eqnarray}
ドナーが全てイオン化していると仮定。\(N_{D}^{+}=N_{D}\)とし、式(10)を式(2)を代入すると
\begin{eqnarray}n(n-N_{D})=n_{i}^{2}\end{eqnarray}
これを、解の公式を用いてnを求めると
\begin{aligned}n=&\dfrac{1}{2}\left( N_{D}+\sqrt{N_{D}^{2}+4n_{i}^{2}}\right) \\ &=\dfrac{1}{2}( N_{D}+\sqrt{N_{D}^{2}+4N_{c}N_{v}\exp \left( -\dfrac{E_{g}}{kT}\right) }\end{aligned}
ただし、式(12)の第2式の変形には、式(3)を利用した。
これが、熱平衡状態における電子密度nの式です。
ただ、式の形が複雑で、結局どのくらい電子密度が高いのか分かりません。
そこで、下記の節では、(i)高温領域、(ii)中間領域、(iii)低温領域 における電子密度nを考えます。各温度条件によって\(N_{D}\)に何かの近似式を与えてやれば、nの関係式を簡素化でき、イメージしやすくなります。
高温領域のとき (真性領域) \(kT >> E_{c}-E_{D}\)
伝導帯の電子\(n\)と価電子帯の正孔\(p\)は、殆ど熱励起していると考えられる。
これがドナー密度\(N_{D}\)より大きいので、\(N_{D}<<\sqrt {np}\) で近似できる。よって、式(12)の\(N_{D}\)は無視できる。
\begin{eqnarray}n= \sqrt{N_{c}N_{v}}\exp(-\dfrac{E_{g}}{kT})\end{eqnarray}
これは、真性半導体の場合と変わりません。真性領域とも言います。
中間領域のとき (出払い領域)
ドナーによる熱励起が支配的になるため、\(N_{D}>>\sqrt {np}\) で近似できる。
式(12)の\(N_{c},N_{v}\)項は無視できるため
\begin{eqnarray}n=\dfrac{N_{D}+ \sqrt{N_{D}^{2}}}{2}=N_{D}\end{eqnarray}
ドープした全てのドナーが、伝導帯へ励起した(出払った)と考えられます。外因性領域とも言います。
低温領域のとき (不純物領域) \(kT << E_{c}-E_{D}\)
温度が非常に小さいとき、ドナーの熱励起が発生しなくなるため、\(N_{d}^{+}=N_{d}\)の前提は使用できない。よって、式(12)は使用できない。
また、中間領域同様に、価電子帯からの電子の励起も無い。このため、正孔の密度\(p=0\)になる。
ドナー準位における電子密度を、フェルミ・ディラックの分布関数\(f_{D}(E_{D})\)を使用して考える。\(f_{D}(E_{D})\)を下記の式で仮定する。
\begin{eqnarray}f_{D}(E_{D})=\dfrac{1}{1+A(E_{D})}\end{eqnarray}
ドナー密度\(N_{D}\)をかけることで、ドナー準位における電子密度は、\(N_{D}f_{D}(E_{D})=\dfrac{N_{D}}{1+A(E_{D})}\)で表される。
これを式(8)に代入すると、
\begin{eqnarray}n=N_{D}-N_{D}\dfrac{1}{1+A(E_{D})} \end{eqnarray}
式(16)を変形すると、
\begin{align}\dfrac{n}{N_{D}-n}&=\left( 1-\dfrac{1}{1+A(E_{D})} (1+A(E_{D}) \right) \\ &=A(E_{D}) \end{align}
縮重状態を考慮したフェルミ・ディラック分布を用いる。\begin{eqnarray}A(E_{D})=\dfrac{1}{2}\exp \left(\dfrac{(E_{D}-E_{F})}{kT}\right)\end{eqnarray}とし、式(20)の両辺に\(n\)をかけると
\begin{align} \dfrac{n^{2}}{N_{D}-n} &= nA(E_{D}) \\ &= \dfrac{1}{2} \exp \left(\dfrac{(E_{D}-E_{f})}{kT}\right) N_{c} \exp \left(-\dfrac{(E_{c}-E_{f})}{kT} \right) \\ &= \dfrac{N_{c}}{2} \exp \left( \dfrac{(E_{D}-E_{c})}{kT} \right) \end{align}
低温領域のとき、\(N_{D}>>n\)であるので、下記のように近似できる。
\begin{eqnarray} \dfrac{n^{2}}{N_{D}-n} = \dfrac{n^{2}}{N_{D}} \dfrac{1}{1-\dfrac{n}{N_{D}}}=\dfrac{n^{2}}{N_{D}}\end{eqnarray}
式(22)に代入し
\begin{align}\dfrac{n^{2}}{N_{D}}= \dfrac{N_{c}}{2} \exp \left( \dfrac{(E_{D}-E_{c})}{kT} \right) \\ n^{2}=\dfrac{N_{c}N_{D}}{2} \exp \left( \dfrac{(E_{D}-E_{c})}{kT} \right) \\ n= \sqrt{\dfrac{N_{c}N_{D}}{2}} \exp \left( \dfrac{(E_{D}-E_{c})}{2kT} \right) \end{align}
であり、低温領域における電子密度\(n\)が求められた。
\(E_{D}<E_{c}\)より、温度を上げた分だけ\(\exp\)項は大きくなる。⇒電子密度は上昇する。
これを凍結領域とも言います。
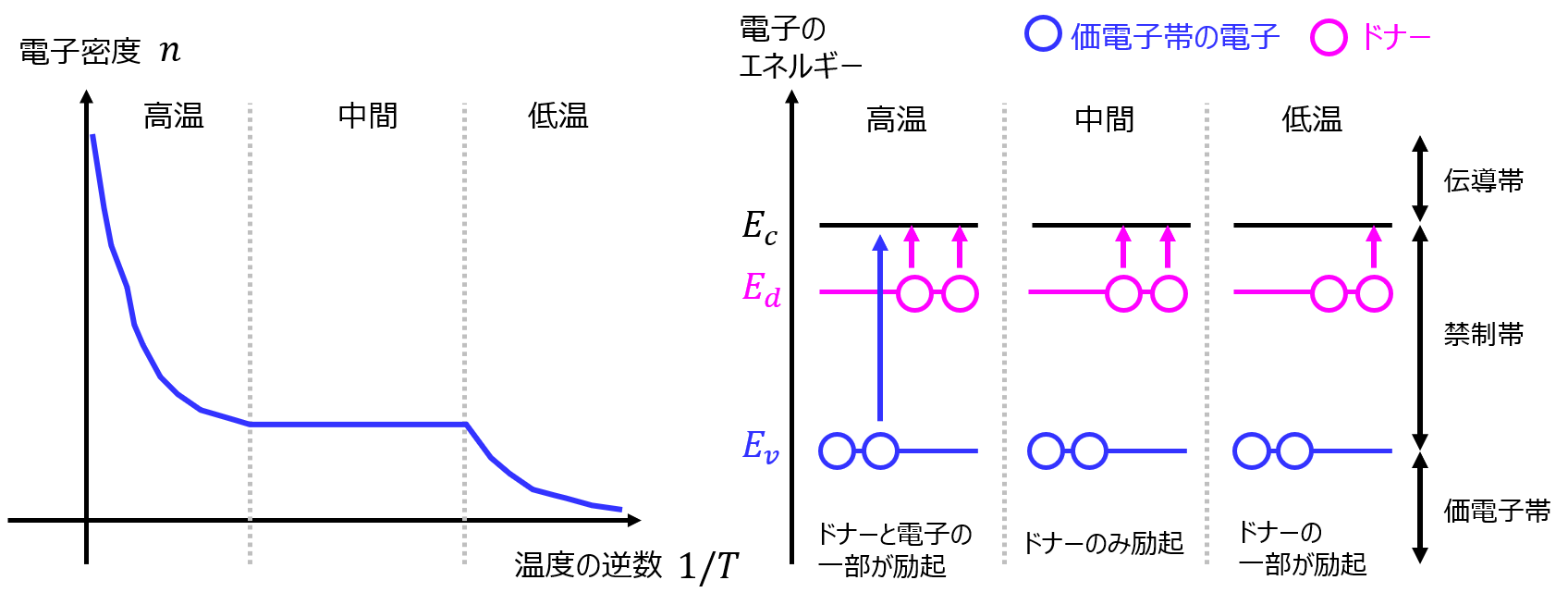
温度と電子密度の関係
前節により、各温度領域における電子密度の関係式が求められました。式(15)(16)(28)
これを、片対数グラフにプロットすると以下のようになります。
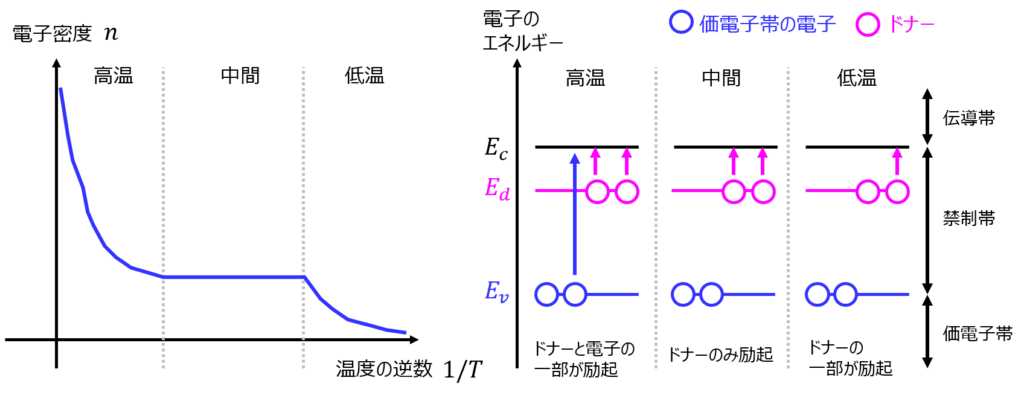
- 高温領域は、価電子帯にある電子が励起するほどのエネルギーが与えられるため、電子密度は上昇する。
- 中間領域は、ドナー準位にある電子は既に出払っているが、価電子帯にある電子が励起するほどではないため、一定値を取る
- 低温領域は、ドナー準位にある電子が伝導帯へ励起するため、電子密度は上昇する。
以上のようにまとめられます。
最後に
バンド構造を題材に試験問題を作成する際、必ず問われる内容になります。試験範囲に入っている大学院を受ける方は、この記事を通して理解を深めて下さると幸いです。
式(19)で仮定する分布関数の形によっては、式(26)と同じ答えにならない場合もあります。是非、問題文に沿って解いていくと良いと思います。
なお、熱平衡状態時のn型半導体の伝導電子密度は下記で表すことができます。(熱平衡状態時)
\begin{eqnarray}n=N_{d}=n_{i}\exp \left(\dfrac{E_{d}-E_{i}}{kT} \right)\end{eqnarray}
また、p型半導体の価電子帯正孔密度は下記式で表せます。
\begin{eqnarray}p=N_{A}=n_{i}\exp \left(\dfrac{E_{i}-E_{a}}{kT} \right)\end{eqnarray}
こちらの内容も問われることがあります。式(1)とは逆に、マイナスをつけずに(準位が上のエネルギー)-(準位が下のエネルギー)と覚えると良いです。
参考文献
半導体デバイス(series電気・電子・情報系):松波 弘之(著) 第1章