 情報
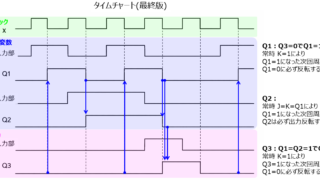
情報 相手に伝わるタイムチャートの書き方を例題形式で解説
タイムチャートの書き方信号が変化するタイミングで縦線を引き、同じ時間で変化している他の信号を明確にする。波形と波形の間に矢印を追記し、信号の入出力関係を明確にする定義元の信号は上に、参照側の信号は紙面下に書く複数の信号である小機能を実現している際は、グループ化する
 情報
情報  情報
情報  情報
情報  情報
情報 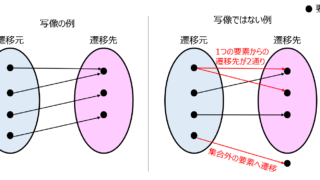 情報
情報 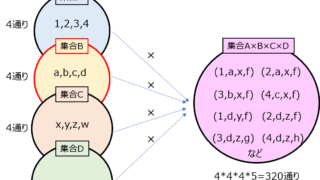 情報
情報 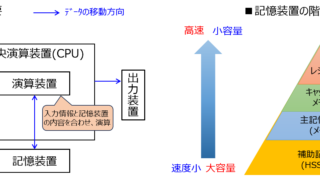 情報
情報 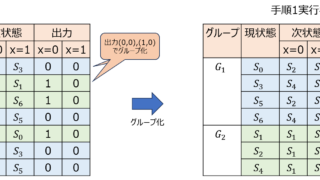 情報
情報 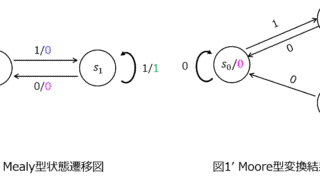 情報
情報 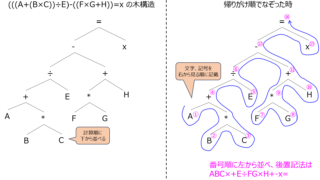 情報
情報