 制御工学
制御工学 伝達関数の簡単化方法のまとめ(例題付き)
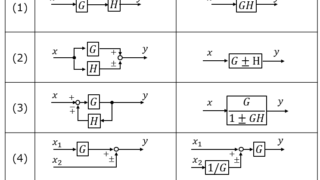
伝達関数の簡単化院試や電検二種をはじめとする制御の問題が出題されるとき、序盤で伝達関数を求めることがよくあります。よく教科書では、下記の表でまとめられています。
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学