 数学
数学 確率変数の積率母関数と最尤推定値の計算問題
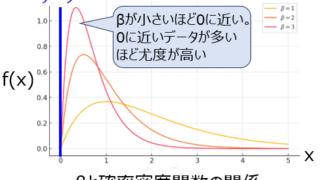
積率母関数確率分布のモーメントを生成する関数で、確率分布の性質を評価するために使用します。最尤推定値観測データが最も起こりやすくなるパラメータを言います。
 数学
数学  数学
数学  数学
数学  数学
数学 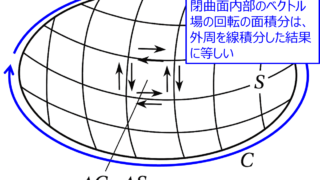 数学
数学 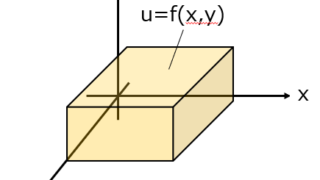 数学
数学 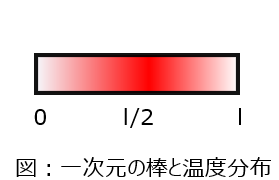 数学
数学 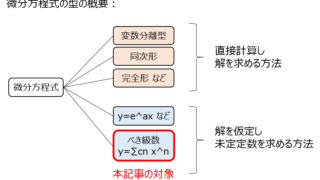 数学
数学  数学
数学  数学
数学