 通信
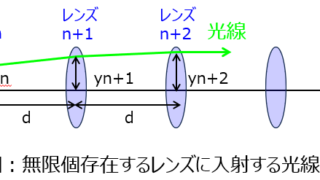
通信 無限個存在する凸レンズに入射する光線の逸脱条件
凸レンズとは中心が厚く、ある一点(焦点)に光を集める性質のある透明体を言います。中心部分ではほぼ平面に近く、光は殆ど曲がらないですが、端部では斜面になっているため、入射光は焦点へ屈折します。
 通信
通信  通信
通信  通信
通信  通信
通信  通信
通信  通信
通信  通信
通信  通信
通信  通信
通信  通信
通信