下記の算術式(中置記法)を、逆ポーランド記法(後置記法)に変換せよ。
\((P-Q÷R)*T+(U÷V-W)+S=A\)
逆ポーランド記法とは
2+3 → 23+ のように、数値を左に配置し、計算するタイミングで演算子を記載する記法です。後置記法(Reverse Polish Notation)とも呼ばれます。
通常、私たちが記載している算術式の記載方法は中置記法です。
人間の目で見て分かりやすいですが、(2+3)/5 の計算を計算機が優先順位を付けて計算することができません。
一方で、後置記法で23+5/のように、計算順に最初から並べている場合を考えましょう。計算機としては左から順に計算していくだけで良いので、処理が楽です。
このように、計算機の計算に適した書き方になります。
中置記法→逆ポーランド記法の書き方
数値(文字)を左から並べていき、優先度順に演算子を並べる方法
こちらで解く方が多いです。
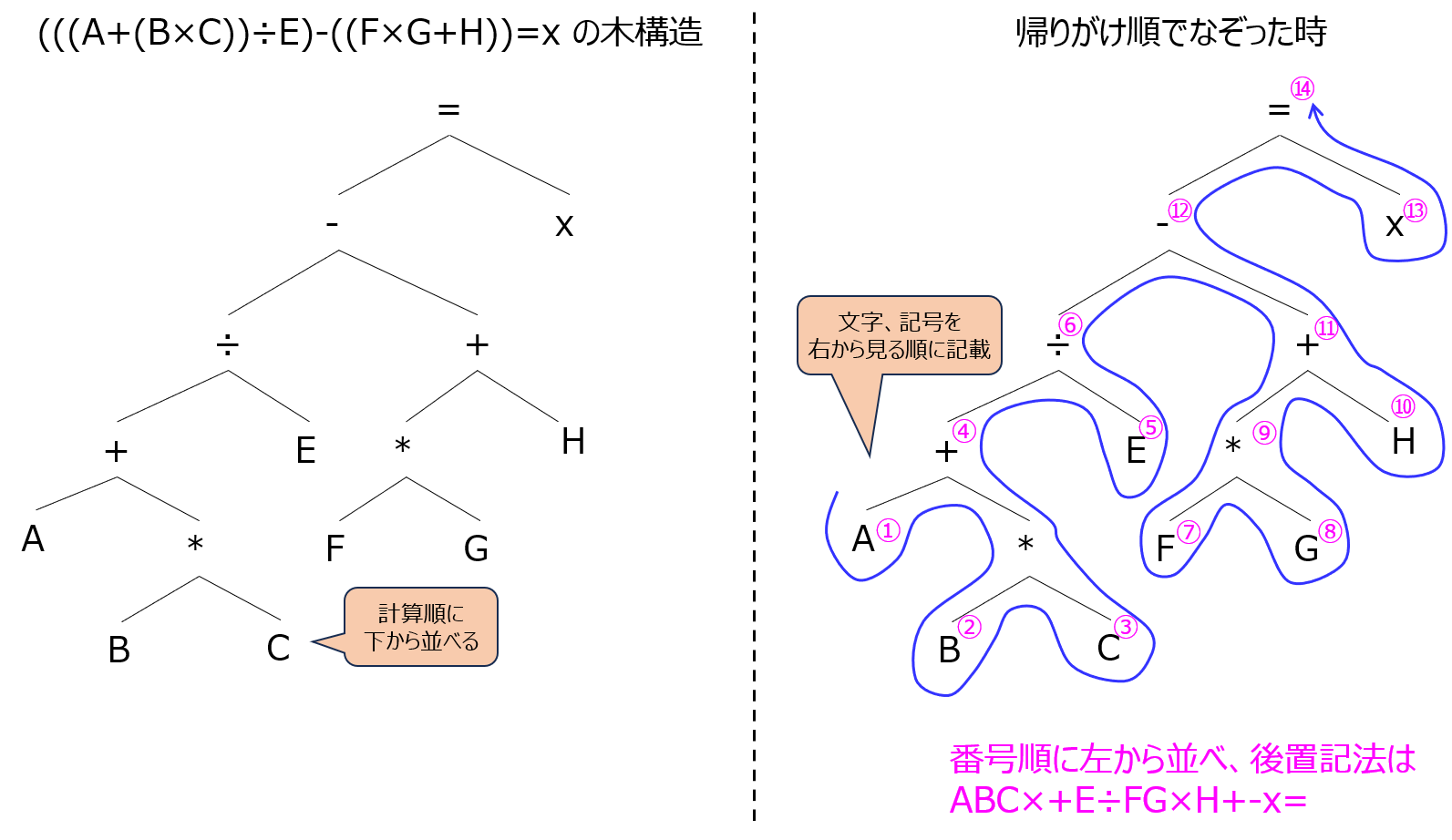
例) (((A+(B×C))÷E)-((F×G+H))=x の場合
まず、左から順に文字を並べ、ABC・・・となります。
続いて、ABCE・・・と並べたいところですが、ここでストップです。
B×Cを一番最初に計算し、次にAを足すため、ABC×+になります。
次にEを割り、-((F×G+H))を計算します。
同様にして、ABC×+E÷FG×H+-x= となります。
※括弧()については、無視します。なぜなら、人間の目で見て括弧の優先度順に演算子を配置しているからです。
木構造を作成し、帰りがけ順で記載する方法
前節と似たような方法になりますが、木構造から求める方法もあります。
優先度が高いほど下に記載していくので、前節と同じ数式を木にすると、下記になります。
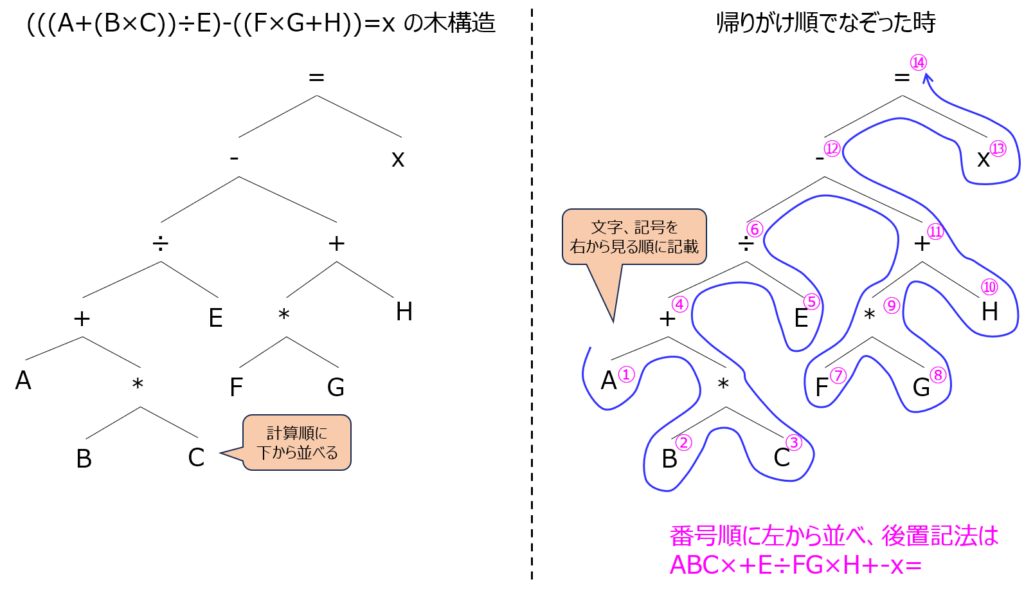
これを帰りがけ順でなぞると、同じくABC×+E÷FG×H+-x=になります。
※帰りがけ順は、木の外側を左からなぞっていき、ノードを左から見る順番で記載していく方法になります。(post-orderとも呼ばれます。)
解答例 \((P-Q÷R)*T+(U÷V-W)+S=A\) の後置記法
数値(文字)を左から並べていき、優先度順に演算子を並べる場合
先の数式の計算順序を考えると、下記になります。
- QをRで割る
- Pを引く
- Tをかける
- UをVで割る
- Wを引く
- Sを足す
- 3の結果を足す
- =でAを結ぶ
左から文字を並べていき、計算のイベントが来るタイミングで演算子を置くと
PQR÷-T×SUV÷W-++A= になります。
木構造を作成し、帰りがけ順で記載する方法
一例ですが、下記(左)のようになります。帰りがけ順でなぞった場合も下図(右)に示します。
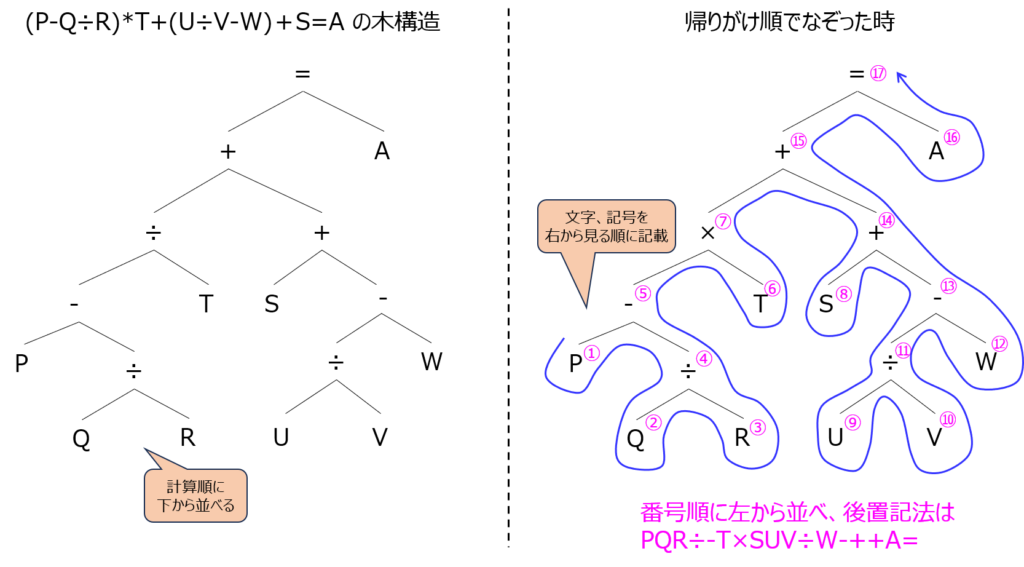
同じ結果になることがわかりました。
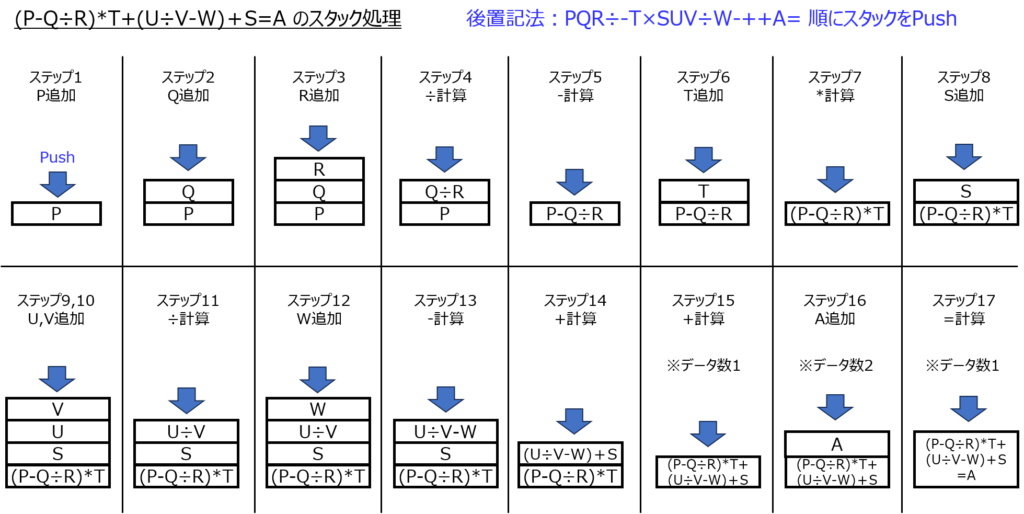
補足:スタックでの処理の流れ
後置記法は、スタックを用いた後入れ先出し方式(LILO:Last In First Out)の処理と同じです。
そのため、処理の流れは下記の図で示すことができます。
(これも、稀に試験問題として出てきます。できるようになっておきましょう。)
最後に
逆ポーランド記法は、院試だけでなく、基本情報、応用情報の資格試験においても頻出分野になります。
将来の仕事に対しても使用する場面が出てくるため、必ずマスターしましょう。