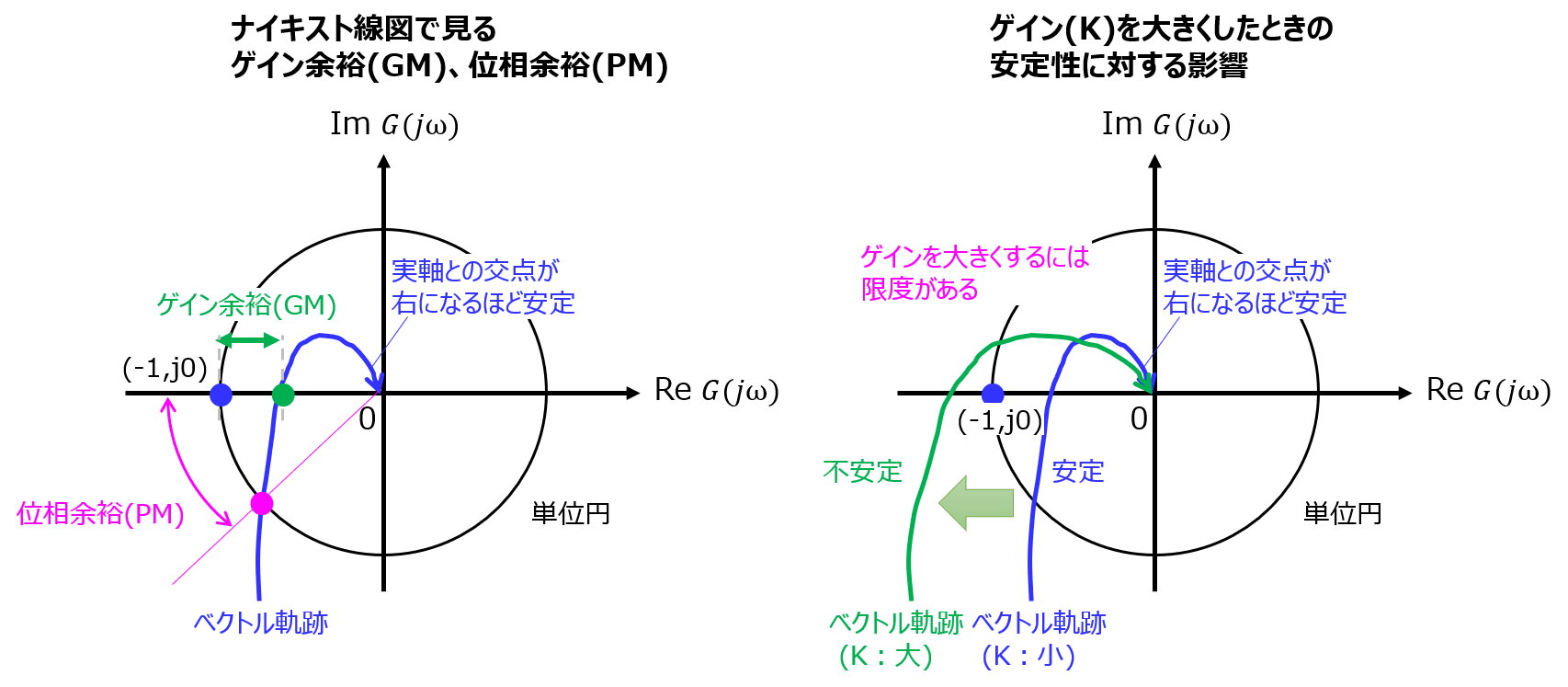
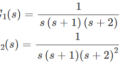下記のような制御系を考える。伝達関数\(G\left( s\right) =\dfrac{s+\sqrt{3}}{\left( s+1\right) ^{2}}e^{-Ls}\)で与えられる。ここで、\(L>0\)である。図(b)は、図(a)の系において\(G(s)\)の前にゲイン要素\(K>0\)を挿入したものである。次の問いに答えよ。
東北大学 電気情報系 院試 2014年8月 専門科目(電気工学) から引用 一部記載を修正
(1)周波数伝達関数\(G(j \omega)\)の絶対値\(\left| G\left( j\omega \right) \right|\)と位相角\(\angle G\left( j\omega \right)\)を求めよ。
(2)図(a)において、\(\left| G\left( j\omega \right) \right|=1\)となる周波数、すなわちゲイン交差周波数\(\omega _{c}\)を求めよ。
(3)図(a)において、位相余裕\(PM[rad]\)を\(L\)で表せ。
(4)図(a)において、\(\angle G\left( j\omega \right) =-\pi [rad]\)となる周波数、すなわち、位相交差周波数を\(\omega_{\pi}\)とする。\(\omega_{\pi}=\sqrt{3}\)となるようなむだ時間\(L\)をを求めよ。
(5)図(a)において、\(\omega_{\pi}=\sqrt{3}\)とする。ゲイン余裕\(GM[rad]\)を求めよ。
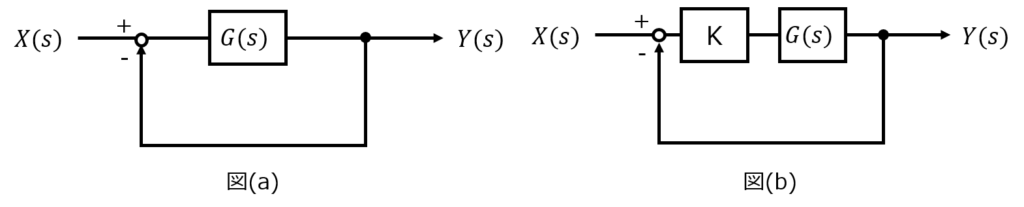
ゲイン余裕(GM)、位相余裕(PM)とは
制御系が安定であるとき、余裕の程度を定量的に表す指標です。
ゲイン余裕は、英訳すると(Gain Margin)のため、GMで略されます。
位相余裕は、英訳すると(Phase Margin)のため、PMで略されます。
それぞれ、ナイキスト線図、ボード線図両面から説明することができます。
ナイキスト線図から見るゲイン余裕(GM)、位相余裕(PM)
以前の記事でも説明しましたが、伝達関数を周波数領域に落とし込んだ時、ベクトル軌跡が(-1,0)より内側(右側)を通れば安定になります。
理由についてはリンク先を参照ください。(ただし、内容は難しいです。一旦そういうもんだと思って本記事を読み進めると良いかもしれません。)
安定性について、(-1,0)の内側を通れば何でも良いわけではありません。例えば、(-1,0)上を通ると安定限界で、システムへの外乱により不安定になってしまうこともあります。
また、制御系の応答性が悪いとき、改善案としてゲイン要素(K)を入れると不安定領域へベクトル軌跡がずれ込みます。よって、大きくできるゲイン要素の量にも限度があります。
この時、ゲイン余裕、位相余裕を定量的に求めていると、ゲインも含めた最適な制御設計ができます。
ナイキスト線図だと、下記のように表すことができます。
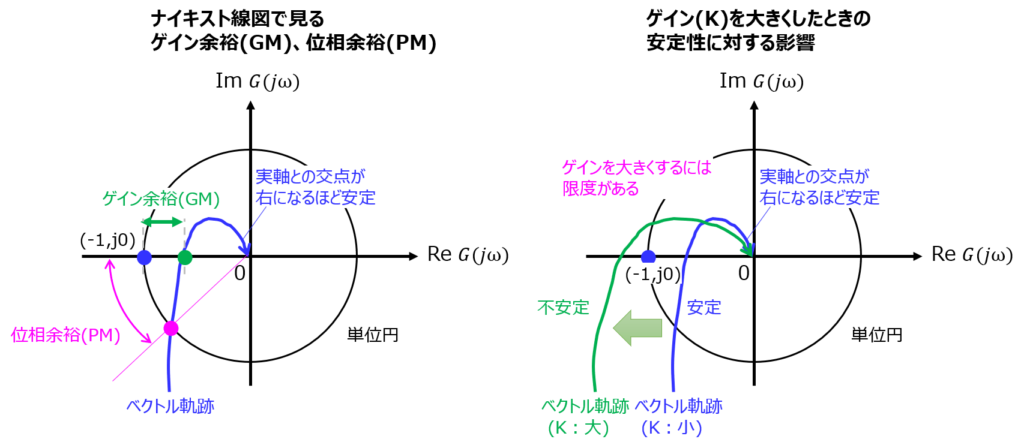
- ゲイン余裕は、実軸を横切った時の座標が、(-1,j0)からどの程度離れているか。
- 位相余裕は、単位円との交点が、どれくらい実軸に対し離れているか。
なお、1.を与える周波数をゲイン交差周波数\(\omega_{c}\)
2.を与える周波数を位相交差周波数\(\omega_{\pi}\)と言います。(2)(4)で使います。
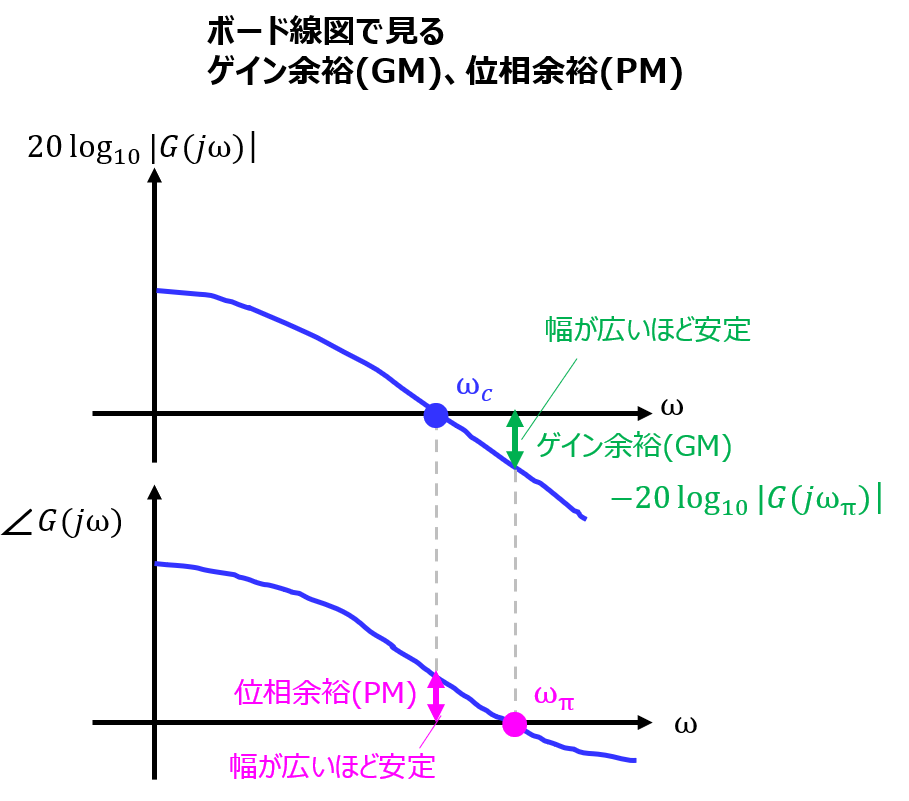
ボード線図から見るゲイン余裕(GM)、位相余裕(PM)
ボード線図は、ナイキスト線図を横軸周波数、縦軸をゲイン、位相に置き換えたものです。
考え方自体はナイキスト線図と変わりません。注意点として、ゲインの単位は[dB]のため、\(|G(j \omega)|=1\)のとき[dB]換算だと0になります。よって、横軸との交点がゲイン余裕に対応します。
解答
前章で基本的な考え方は述べました。院試問題を引用したため面食らうかもしれませんが、基本的な計算で解決します。
(1)周波数伝達関数と位相角
\(s=j\omega\)として、周波数伝達関数を求める。
\begin{eqnarray}G\left( s\right) =\dfrac{s+\sqrt{3}}{\left( s+1\right) ^{2}}e^{-Ls}\end{eqnarray}
\begin{aligned}G\left( j\omega \right) &=\dfrac{j\omega +\sqrt{3}}{\left( j\omega +1\right) ^{2}}e^{-j\omega L} \\ &=\dfrac{j\omega +\sqrt{3}}{\left( (1-\omega^{2}) +2j \omega \right) }e^{-j\omega L} \end{aligned}
オイラーの式より、\(\left| e^{-j\omega L}\right| =1\)なので
\begin{eqnarray}\left| G\left( j\omega \right) \right| =\dfrac{\sqrt{3+\omega ^{2}}}{\sqrt{\left( 1-\omega ^{2}\right) +4\omega ^{2}}}\end{eqnarray}
\begin{aligned} \angle G\left( j\omega \right) =\tan ^{-1}\left( \dfrac{\omega }{\sqrt{3}}\right) -2\tan ^{-1}\left( \omega \right) -\omega L\end{aligned}
(2)ゲイン交差周波数
(3)式が1になれば良い。(1)より
\begin{aligned} \angle G\left( j\omega \right) =\tan ^{-1}\left( \dfrac{\omega }{\sqrt{3}}\right) \\ -2\tan ^{-1}\left( \omega \right) -\omega L\end{aligned}
\(\omega >0\)で、虚数では無いので、\(\omega_{c}=1\)
(3)位相余裕
\( PM=\pi +\angle G\left( j\omega _{c}\right) \) で(5)より
\begin{aligned}PM&=\pi +\tan ^{-1}\left( \dfrac{1}{\sqrt{3}}\right) -2\tan ^{-1}\left( 1\right) -L \\ &= \pi +\dfrac{\pi }{6}-2\cdot \dfrac{\pi }{4}-L \\ &=\dfrac{2 \pi}{3} – L \end{aligned}
(4)位相交差周波数
\(\omega _{\pi }=\sqrt{3}\)より、(5)式から
\begin{aligned}\angle G\left( j\omega \right) &= \tan ^{-1}\left( 1\right) -2\tan ^{-1}\left( \sqrt{3}\right) -\sqrt{3}L \\ &= -\pi \\ -\sqrt{3}L&=-\pi -\dfrac{\pi }{4}+\dfrac{2}{3}\pi \\ L&=\dfrac{7}{12\sqrt{3}}\pi \end{aligned}
(5)ゲイン余裕
\(GM=-20\log 10\left| G\left( j\omega _{\pi}\right) \right|\)で、
\begin{eqnarray}\left| G\left( j\omega _{c}\right) \right| =\dfrac{\sqrt{3+3}}{\sqrt{4+12}}=\dfrac{\sqrt{6}}{4}\end{eqnarray}なので、
\begin{aligned}GM &=-20\log_{10} \dfrac{\sqrt{6}}{4} \\ &= -10 \log_{10}3-10\log_{10}2+40 \log_{10}2 \\ &=-10*0.5+30*0.3 \\ &= 4\end{aligned}
最後に
安定性に関する問題は、ナイキスト線図、ボード線図、どちらからでも問われます。本問を通して、練習していただければと思います。