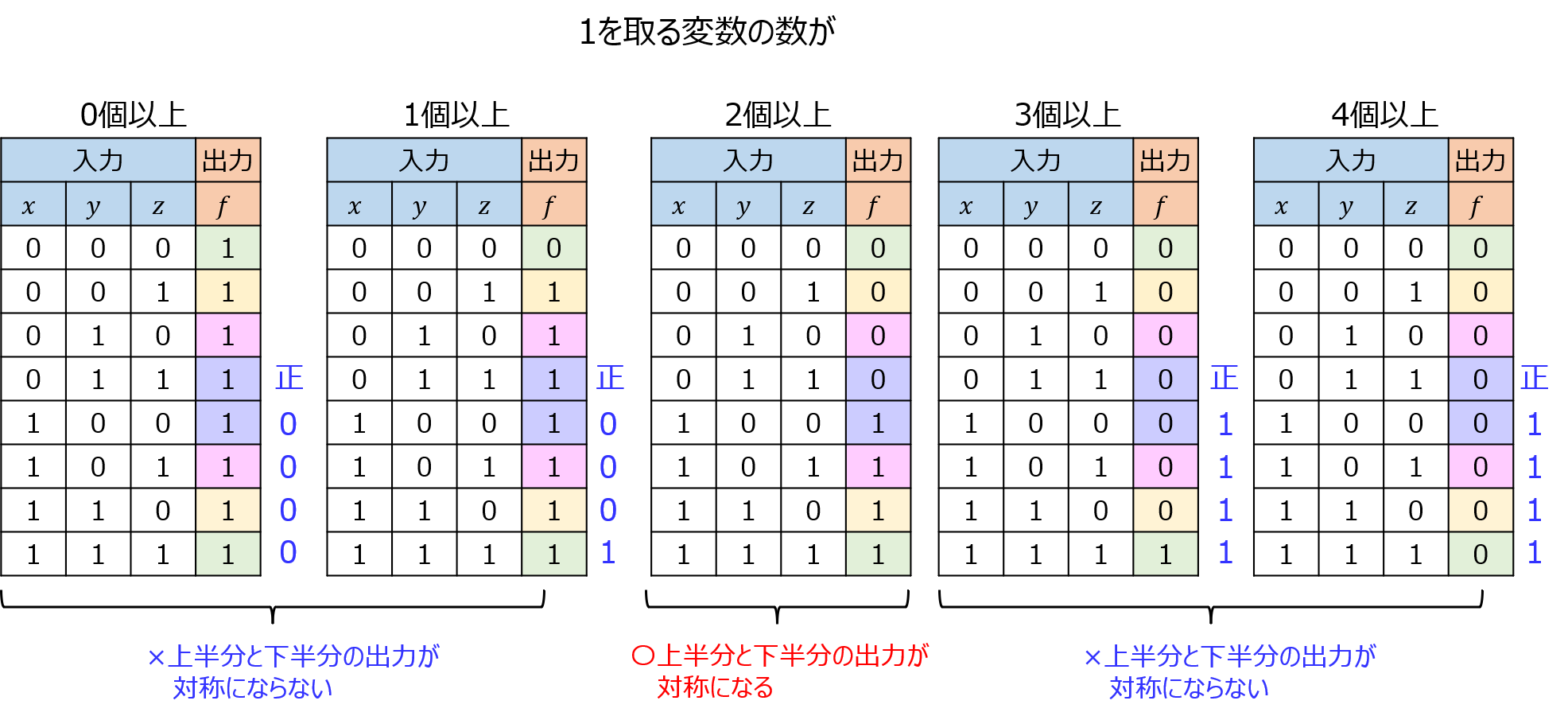
\begin{aligned}f\left( x_{1},x_{2},\ldots ,x_{n}\right) =c_{1}x_{1}+c_{2}x_{2}+\ldots +c_{n}x_{n}\geq T\end{aligned}
が成立するとき、\(f\)は閾値関数と言う。次の問いに答えよ。
(1)任意の\(i\)について\(c_{i}=1\)のとき、閾値関数の双対関数は単調増大関数であることを証明せよ。
(2)(1)のとき、n変数閾値関数の双対関数と閾値Tの関係を求めよ。
(3)単調増大かつ自己双対である3変数論理関数を示せ。
(4)単調増大かつ自己反双対であるn変数論理関数を示せ。
本記事で覚えたいこと
- 閾値関数は、1を取る変数の数が一定個数(T)以上のとき、必ず1を取る。
- 逆に、1を取る変数の数が一定個数未満のとき、必ず0を取る。
- 自己双対(関数の否定)を取ると、n-T個以下のとき、必ず0を取るようになる。

3.のように、関数の否定を取ると、閾値が変化する点に注目です。
上記の事実は、(1)(2)を解くうえで使います。(3)(4)は、自己双対関数の記事で扱ったように、真理値用を記載していくことで解決できます。
解答例
(1)(2)n変数閾値関数の双対関数
変数\(x_{i}=1\)を取る\(i\)の個数を\(N(x_{1},x_{2}, \ldots,x_{n}\)とすると、閾値関数の定義より、以下の式が成立する。
\begin{eqnarray}N(x_{1},x_{2}, \ldots,x_{n})≧T\end{eqnarray}
これの双対関数が1を取るとき、下記の式が成立する。
\begin{eqnarray}N(\overline{x_{1}},\overline{x_{2}}, \ldots,\overline{x_{n}})<T \\ n-N(x_{1},x_{2}, \ldots,x_{n}) <T\end{eqnarray}
このとき、
\begin{eqnarray}F( \overline{x_{0}},\overline{x_{1}},\overline{x}_{2},\ldots ,\overline{x_{n}})=0\end{eqnarray}
なので、
\begin{eqnarray}F_{d}(x_{0},x_{1},x_{2},…,x_{n})=\overline{F( \overline{x_{0}},\overline{x_{1}},\overline{x}_{2},\ldots ,\overline{x_{n}})}=1\end{eqnarray}
が成立する。
(5)式を整理すると
\begin{eqnarray}n-T<N(x_{1},x_{2}, \ldots , x_{n}\end{eqnarray}
よって、\(F_{d}\)は閾値n-T+1の単調増大関数であることが示された。
(3)単調増大かつ自己双対の3変数論理関数
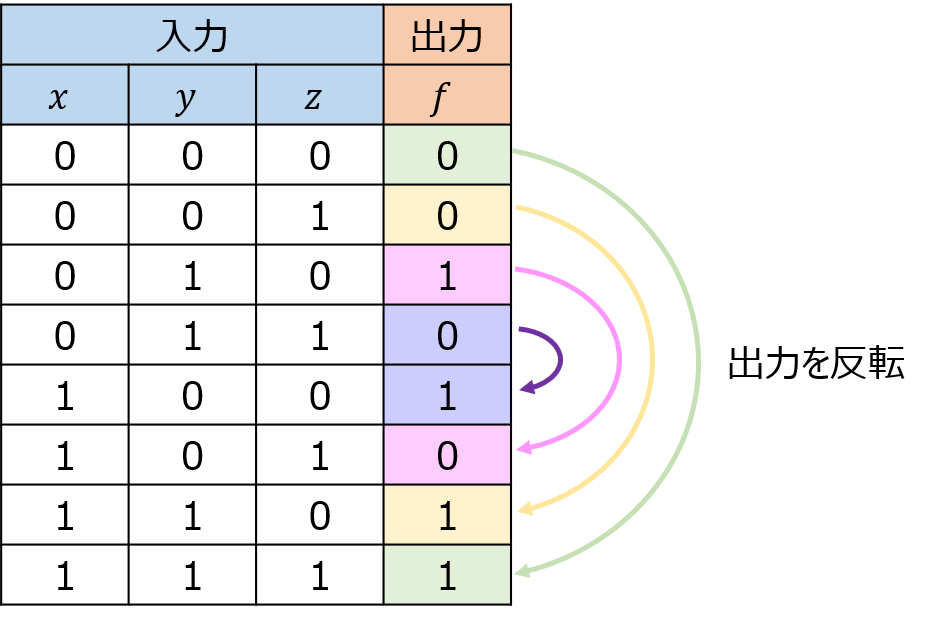
自己双対関数の性質により、真理値表の上半分が決定すると、下半分は、上半分の出力にNOTを取った値が出力される。
単調増大のとき、\(x_{i}=1\)を取る変数が0個以上、1個以上、2個以上、3個以上の4通りある。下記により、2個以上の場合のみ題意を満たす。
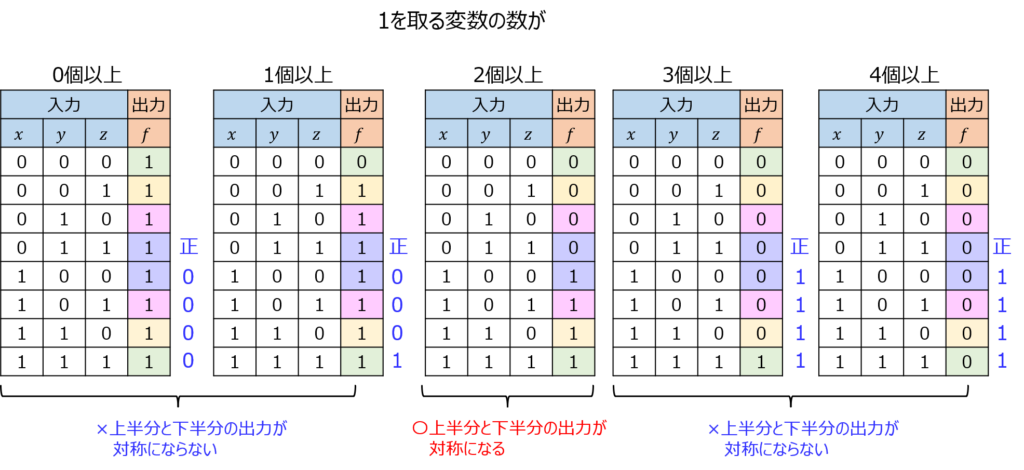
以上より、3変数多数決関数が題意を満たすので、求める論理式は
\begin{eqnarray}f(x_{1},x_{2},x_{3})=x_{1}x_{2}+x_{2}x_{3}+x_{1}x_{3}\end{eqnarray}
(4)単調増大かつ自己反双対のn変数論理関数
題意が成立するとき、以下の関係が成立する。
\begin{eqnarray}f(0,0,\ldots,0)=f(1,1,\ldots,1)\end{eqnarray}
全ての変数が0である場合と1である場合で値が等しい。また、一部の変数が1である場合も同じ値を取らなければならない。
このことから、題意を満たす論理関数は、0値関数か1値関数の2通りのみになる。
最後に
問題によっては、\(c_{1}=1,c_{2}=2\)など、変数に対して重みを付与した場合もあります。どのような式で表記されているか、事前に注意深く確認しましょう。
参考文献
スイッチング回路理論:当麻 喜弘 (著)