n変数線形関数の性質

あるn変数論理関数について、\begin{eqnarray}f\left( x_{1},x_{2},\ldots ,x_{n}\right)=c_{0}\oplus c_{1}x_{1}\oplus c_{2}x_{2}\oplus \ldots \oplus c_{n}x_{n}\end{eqnarray}が成立するとき、線形関数と呼ぶ。(\(c_{i}\quad (i=0,1,2, \ldots , n\))は定数で0か1が入る。)

下記の問に答えよ。
(1)n変数論理関数の中で、n変数線形関数は何個存在するか。
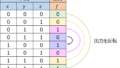
(2)線形関数は、自己双対関数か自己反双対関数のいずれかであることを示せ。
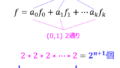
(3)全てのn変数論理関数は、\(c_{0}\oplus X_{1}\oplus X_{2}\oplus \ldots \oplus X_{m}\)型の環和標準形で表されることを証明せよ。但し、\(m\)は任意の自然数

はじめに
この記事で覚えたいこと
解答例
最後に
参考文献

はじめに

論理関数の中には、様々な性質を持つものがあります。例として、前回の記事では、自己双対関数を説明しました。今回は、線形関数について説明します。性質については、本問で述べた通りです。

こちらも、東北大をはじめとする院試でよく出題されます。

この記事で覚えたいこと

n変数線形関数の個数は、\(c_{i}\)に入る値の組み合わせ分存在する。
\(\overline{x_{i}}=1 \oplus x_{i}\)と表すことができる。
完全系(NOR)は環和標準形(XOR)でも表すことができる。

1.2.3.それぞれ(1)(2)(3)で使用します。

XORは排他的論理和です。\(x \oplus y\)が\(x≠y\)のとき、1、\(x=y\)のとき0を出力します。

下記のように分配律が成立します。

\begin{align}NOR(x,y)&=(\overline{x+y}) \\ &=(\overline{x}･\overline{y}) \\ &=(1 \oplus x)(1 \oplus y) \\ &=xy \oplus x \oplus y \oplus 1 \end{align}

確かに、環和標準形で表すことができました。この式変形を利用し、(2),(3)を解いていきます。

解答例

(1) n変数線形関数の個数

問題で与えられた通り、n変数線形関数は、式(1)で表される。

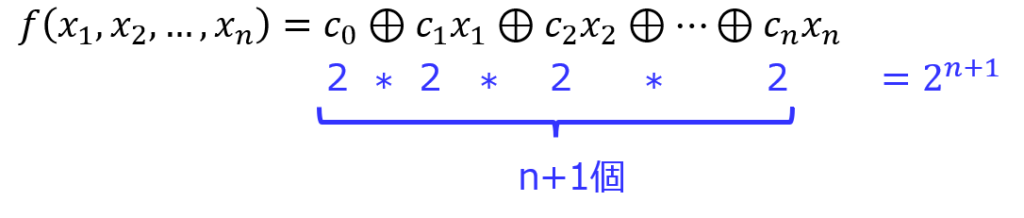
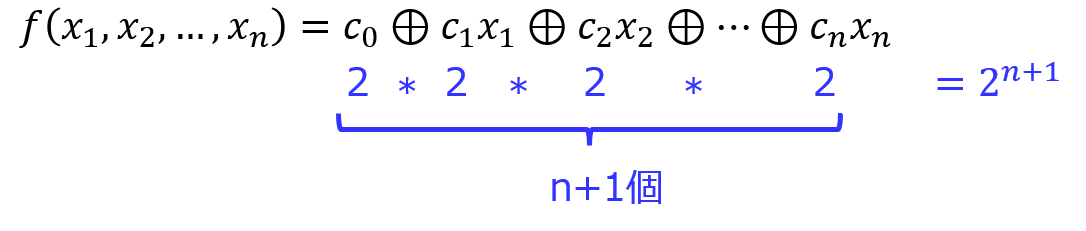
\(c_{i}\)は、0,1の2通り入り、これが\(i=0,1,2, \ldots ,n\)のn+1個の定数に対し当てはめることができる。

よって、\(2*2*2* \ldots 2 = 2^{n+1}\)個存在する。

(2) 線形関数と双対関数

\begin{eqnarray}\overline{x_{i}}=1 \oplus x_{i}\end{eqnarray}を使用して、式(1)を変形する。

\begin{align} f \left( \overline{x_{1}}, \overline{x_{2}}, \ldots , \overline{x_{n}} \right) &= c_{0} \oplus c_{1}\overline{x_{1}} \oplus c_{2}\overline{x_{2}} \oplus \ldots \oplus c_{n}\overline{x_{n}} \\ &= c_{0} \oplus c_{1}(1 \oplus x_{1}) \oplus c_{2}(1 \oplus x_{2}) \oplus \ldots \oplus c_{n}(1 \oplus x_{n}) \\ &= \left( c_{0} \oplus c_{1} \oplus \ldots \oplus c_{n} \right) \oplus c_{1}x_{1} \oplus c_{2}x_{2} \ldots c_{n}x_{n} \end{align}

\(c_{1}x_{1} \oplus c_{2}x_{2} \oplus \ldots \oplus c_{n}x_{n} ･･･(A) \) は線形関数の変数項である。

\(\left( c_{0}\oplus c_{1}\oplus \ldots \oplus c_{n}\right)･･･(B)\) の値次第で(7)式の結果が変化する。

(i) (B)=1 のとき、\(\overline{x_{i}}=1 \oplus x_{i}\) より出力は反転する。

\begin{align}f\left( \overline{x_{1}},\overline{x_{2}},\ldots ,\overline{x_{n}}\right)=\overline{f\left( x_{1},x_{2},\ldots ,x_{n}\right)}\end{align}

これより、自己双対関数であることが示された。

(ii) (B)=0 のとき、\({x_{i}}=0 \oplus x_{i}\) より、入力値を出力する。

\begin{align}f\left( \overline{x_{1}},\overline{x_{2}},\ldots ,\overline{x_{n}}\right)=f \left( x_{1},x_{2},\ldots ,x_{n}\right)\end{align}

これより、自己反双対関数であることが示された。