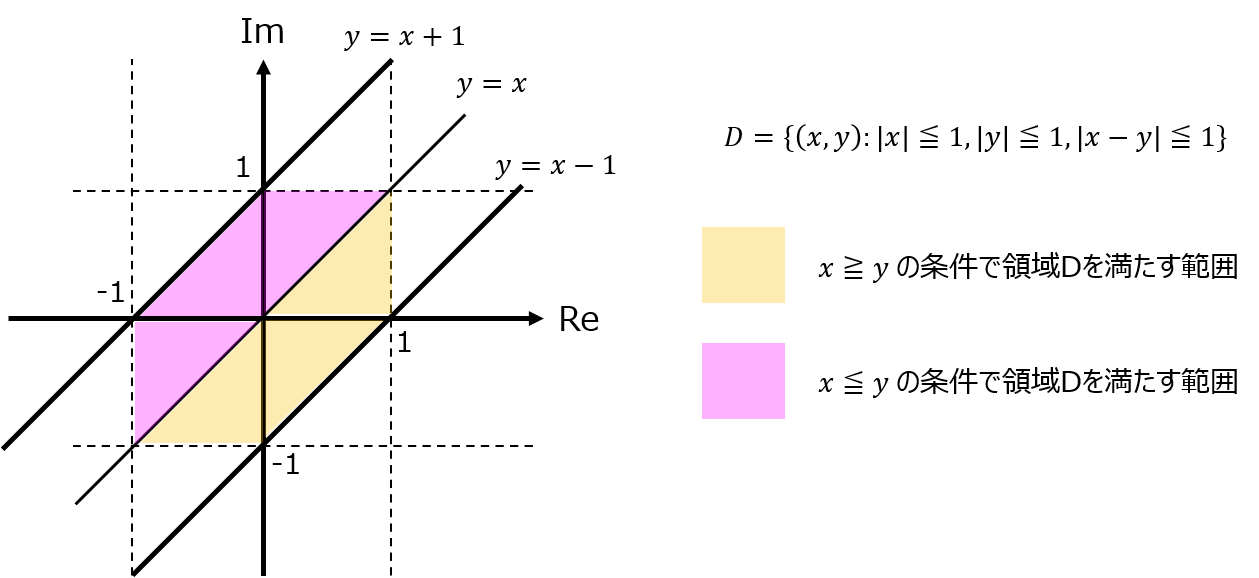【重積分】絶対値付きの領域の計算

実数x,yが領域\(D_{1},D_{2}\)の範囲を取るとき、以下の積分結果\(F_{1},F_{2}\)を求めよ。
\begin{eqnarray}D_{1}:\left\{ \left| x\right| \leqq 1,\left| y \right| \leqq 1,|x-y|\leqq 1\right\} \\ F_{1}=\iint _{D}\left| x-y\right| dxdy \\ D_{2}: \left\{ \left | \dfrac{x}{a}\right| +\left| \dfrac{y}{b }\right| +\left| \dfrac{z}{c}\right| \leqq 1 \right\} \\ F_{2}= \iiint _{D}dxdydz \end{eqnarray}

はじめに

ちょっと複雑めの積分問題です。変数を置き換えるなど、色々な解き方がありますが、本記事では与えられた\(x,y\)の領域\(D\)の条件をそのままに計算した過程を記載します。

本記事で覚えてほしいこと

<絶対値付き領域の積分方針>

よくある高等学校の数学の領域を考える問題と同様の解き方になります。

ただし、2．については慣れが必要と思います。一文字(x)を固定したときにyの取りうる範囲を領域にしていく問題は高校でも行ったと思います。これをもう一度思い出します。

３．については知識として持っておくと良いかもしれません。被積分関数の内容にもよりますが、絶対値のついた問題は、対称性を利用できることが多い印象です。

解答例 (問1)

絶対値を外し、個々の不等式をグラフ化する

絶対値を外すと、領域Dは以下の連立不等式に書き下せる。

\begin{eqnarray}\begin{cases}-1\leqq x\leqq 1\\ -1\leqq y\leqq 1\\ y\leqq x+1\\ y\geqq x-1\end{cases}\end{eqnarray}

これをグラフにすると、以下のようになる。(色が付いている範囲が領域D)

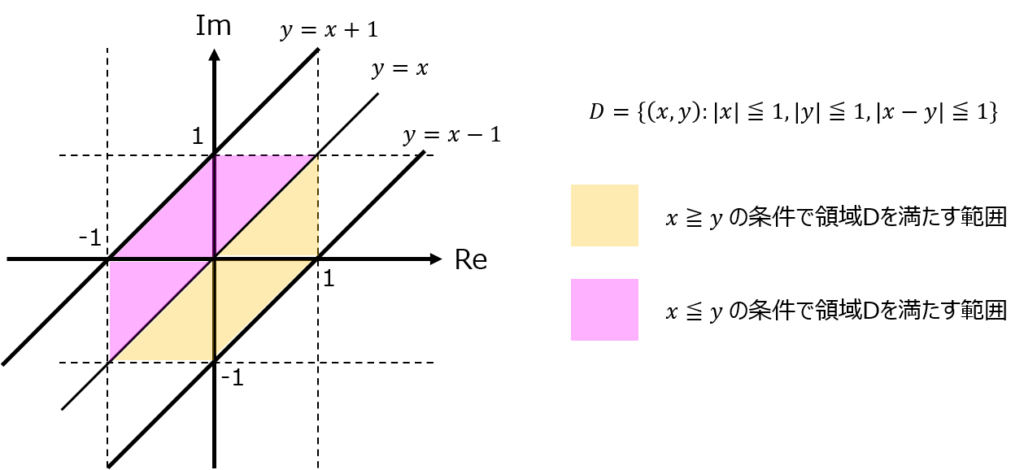
積分範囲の選定

\(x≧y\)の範囲で考える。

黄色の積分範囲をそのまま考えると複雑なため、以下のような領域を取り、求めたい積分範囲を数式化する。

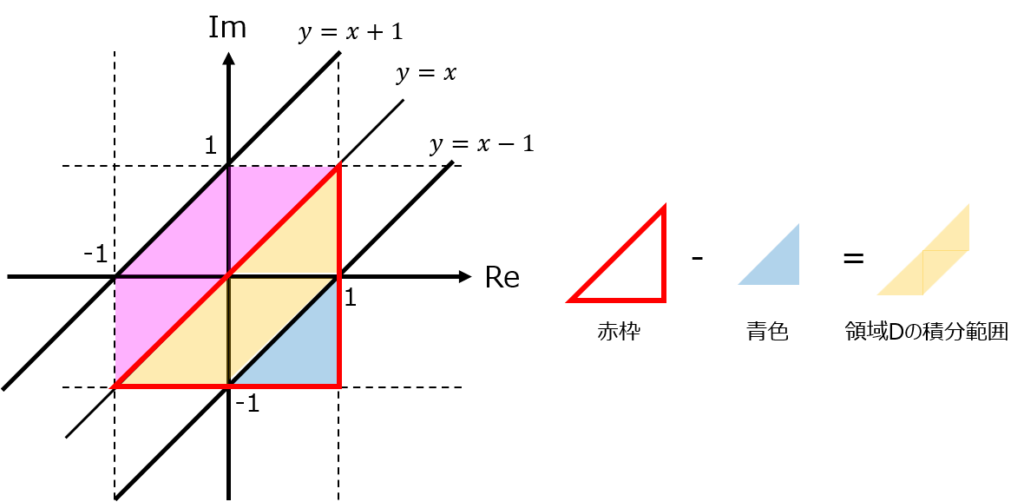
領域Dの半分(黄色範囲)：(赤枠の大三角形)–(青色の小三角形)

・赤枠の大三角形の積分範囲：\((-1≦x≦1,-1≦y≦x)\)
・緑色の小三角形の積分範囲：\((0≦x≦1,-1≦y≦x-1)\)

実際の積分

対称性により、黄色の領域で積分した結果を2倍して、結果Fを求める。

(黄色の領域の積分結果)=(赤枠の大三角形の積分結果)–(青色の小三角形の積分結果) だから

\begin{align}\dfrac{F_{1}}{2}&=\int _{-1}^{1}dx\int _{-1}^{x}\left( x-2\right) dy -\int _{0}^{1}dx\int _{-1}^{x-1}( x-y) dy \\ &= \int _{-1}^{1}dx\left[ xy-\dfrac{y^{2}}{2}\right] _{-1}^{x}-\int _{0}dx\left[ xy-\dfrac{y^{2}}{2}\right] _{-1}^{x-1} \\ &= \int _{-1}^{1}\left( \dfrac{x^{2}}{2}+x+\dfrac{1}{2}\right) dx-\int ^{1}_{0}\left( \dfrac{1}{2}x^{2}+x\right) dx \\ &= \left[ \dfrac{x^{3}}{6}+\dfrac{x^{2}}{2}+\dfrac{x}{2}\right] ^{1}_{-1}\left[ \dfrac{x^{3}}{6}+\dfrac{x^{2}}{2}\right]- ^{1} _{0} \\ &=\dfrac{1}{3}+1-\dfrac{2}{3}\\ &=\dfrac{2}{3} \\ F_{1} &= \dfrac{4}{3} \end{align}

解答例 (問2)

同じく、対称性を利用します。

絶対値を外し、個々の不等式をグラフ化する

式(3)の左辺に注目する。\(\dfrac{x}{a}\)が正である場合、負の場合で取りうる領域が2通り、\(\left( \dfrac{y}{b},\dfrac{z}{c} \right)\)についても同じくそれぞれ2通り存在する。

結局、\(2^{3}=8\)通り考える領域が存在する。式(3)は絶対値を取るため正負の場合によらず、取る式は以下になる。

\begin{eqnarray}\dfrac{x}{a}+\dfrac{y }{b }+\dfrac{z}{c}\leqq 1\end{eqnarray}

下記図のように、\(x≧0,y≧0,z≧0\)の領域①で取る体積を計算し、結果を8倍すると求めたい体積を得られる。

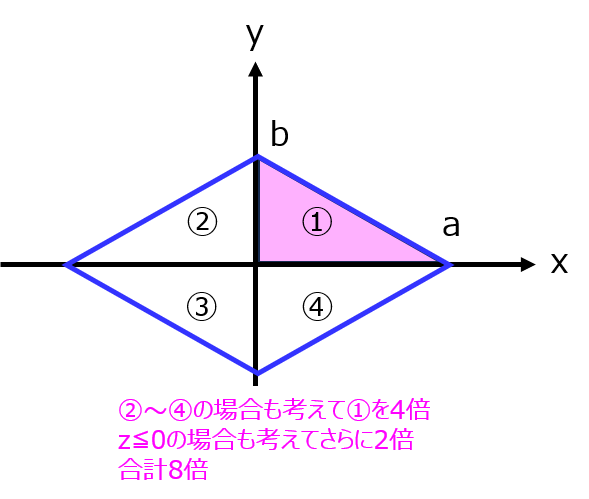
積分範囲の選定

\(0≦x≦a\)動くとすると、\(y\)はxをある値に固定し、\(0≦y≦b \left(1-\dfrac{x}{a}\right)\)の範囲を動く。
\(z\)はx,yをある値に固定し、\(0≦z≦b \left(1-\dfrac{x}{a}-\dfrac{y}{b} \right)\)を動く。

よって、下記の積分を行えば良い。

\begin{align}F_{2}&=\iiint _{D}dxdydz \\ &=8\int ^{a}_{0}dx\int ^{b\left( 1-\frac{x}{a}\right) }_{0}dy\int ^{c\left( 1-\frac{x}{a}-\frac{\partial }{b}\right) }_{0}dz\end{align}

実際の積分

\begin{align}(14)&=8c\int ^{a}_{0}dx\int _{0}^{b\left( 1-\frac{x}{a}\right) }\left( 1-\frac{x}{a}-\frac{y}{b}\right) dy \\ &= 8c\int _{0}^{a}\left[ \left( 1-\dfrac{x}{a}\right) y-\dfrac{y^{2}}{2b}\right] _{0}^{b\left( 1-\frac{x}{a}\right) }dz \\ &=4cb\int _{0}^{a}\left( 1-\dfrac{x}{a}\right) ^{2}dx \\ &=\dfrac{4cb}{3}\left[ -\left( 1-\dfrac{x}{a}\right) ^{3}\right] _{0}^{a} \\ &= \dfrac{4abc}{3}\end{align}

であることが分かった。三角錐の体積を表しています。

類題で、下記の領域の体積を問われることがあります。

\begin{eqnarray}\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\leqq 1\end{eqnarray}

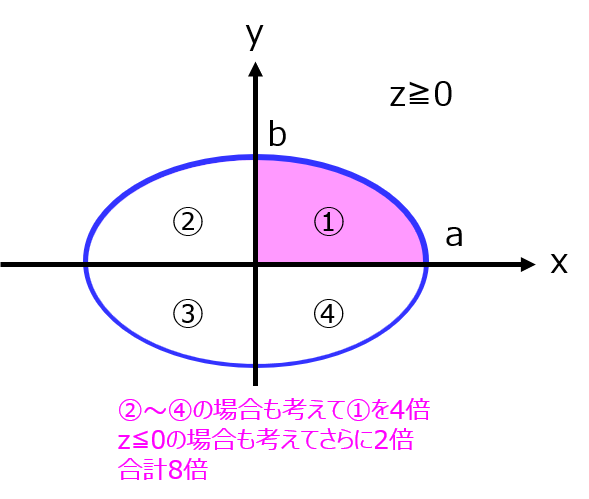
同様の計算を行うことで、\(\dfrac{4 \pi abc}{3}\)になります。

これは、楕円体の体積を表しています。京大、名大で出題されたことがあります。両大学を志望する方は、是非覚えておきましょう。

最後に

今回はまだ計算しやすい領域でしたが、非常に複雑になるケースもあります。他の変数変換手法も説明していきますので、今後ともよろしくお願いいたします。