ドリフト電流、拡散電流とアインシュタインの関係式の導出

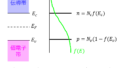
図1は平衡状態にある半導体pn接合のエネルギーバンド図を示している。$x$軸は接合界面に垂直であり、伝導帯底および価電子帯頂上における電子のエネルギーはそれぞれ$E_c(x),E_v(x)$で表される。半導体の禁制帯幅$E_G$、伝導帯の有効状態密度$N_c$および価電子帯の有効状態密度$N_V$は位置によらず一定である。温度は$T$、フェルミ準位は$E_F$、ボルツマン定数は$k_B$、素電荷は$q$である。以下の問いに答えよ。

(1)位置$x$における電子密度$n(x)$を表す式を示せ。

半導体中における電子の拡散係数を$D_e$、ドリフト移動度を${\mu }_e$とする。

(2)位置$x$において電子の拡散に伴う電流密度を求めよ。
(3)位置$x$において電子のドリフトに伴う電流密度を求めよ。
(4)$D_e$と${\mu }_e$の間に成り立つ関係式を求めよ。

東北大学 電気情報系院試 2020/3月 電子工学より抜粋 一部の問題を省略

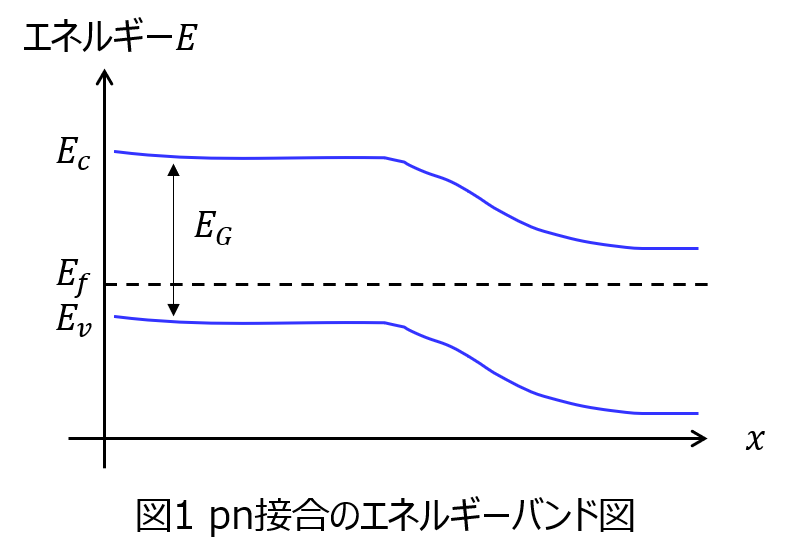
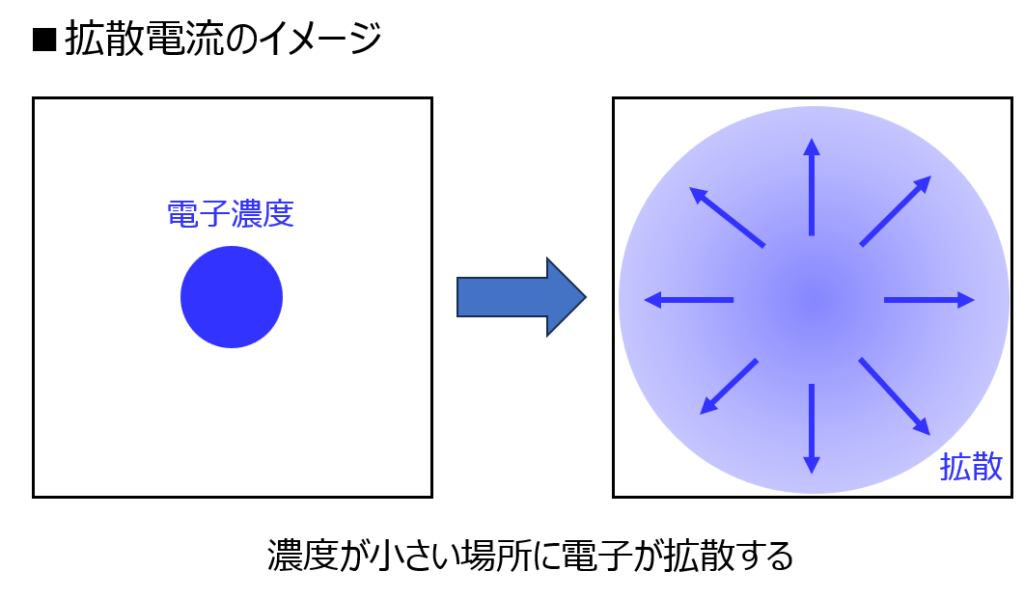
拡散電流とドリフト電流の違い

過去の記事で詳しく解説していますが、ここでも簡潔に説明します。

拡散電流とは

キャリア濃度に分布があるとき、その濃度差を埋めるように流れる電流です。電流値は、濃度勾配に比例し、下記の式で表すことができます。

$$\begin{array}{}\text{(1)}& \begin{array}{r}{I}_D=-q{D}_e{\displaystyle \frac{dn(x)}{dx}}\end{array}\end{array}$$

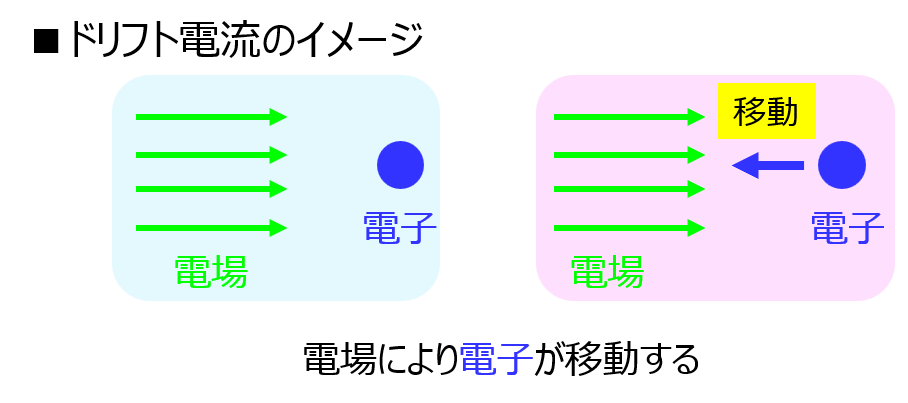
ドリフト電流とは

電場によって電子が動く現象を意味しています。電磁気学でよくある荷電粒子の運動の半導体バージョンですね。

下記の式で表すことができます。

$$\begin{array}{}\text{(2)}& \begin{array}{r}{I}_{\mu }=qn(x){\mu }_{e}E\end{array}\end{array}$$

電界とドリフト電流の関係

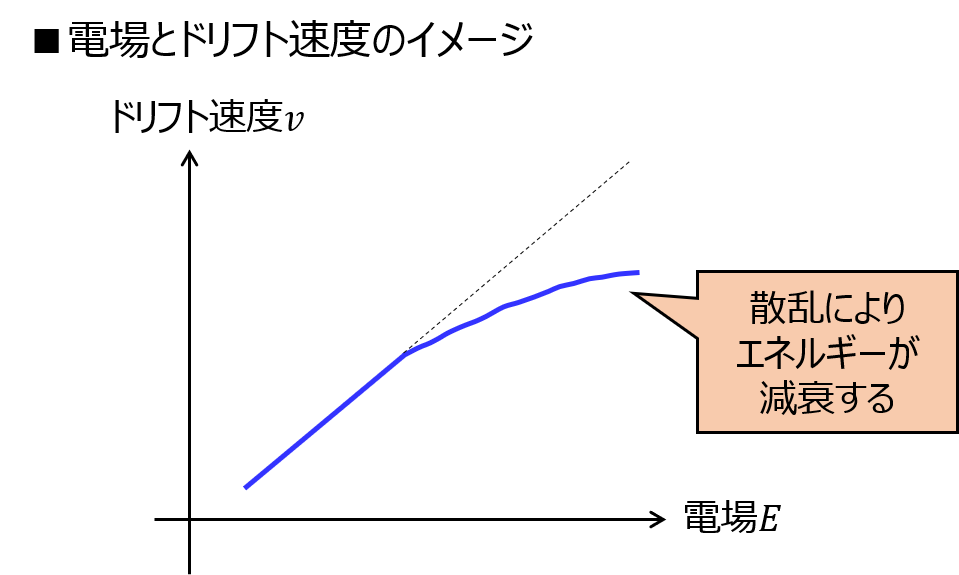
上式だけ見ると、無制限に電場$E$を大きくすれば、それだけ移動度が上がるように見えます。

しかし、実際はそうなりません。

電場を大きくすると、電子の速度は大きくなりますが、その分半導体結晶中の格子と衝突する時間が短くなります。

よって、電場を大きくすると、衝突によりエネルギー損失が大きくなるので、思ったより速度は大きくなりません。

解答例

(1)電子密度

過去の記事より

$$\begin{array}{}\text{(3)}& \begin{array}{r}n(x)=N_c\exp (-{\displaystyle \frac{E_c\left(x\right)-E_f}{k_{B}T}})\end{array}\end{array}$$

※初見だったとしても、上記の式は暗記しておかなければなりません。伝導帯の底にフェルミ準位を引いてexpを取る。Ncを乗する。と覚えましょう。

(2)拡散電流の式

前章より、拡散電流密度は(1)式で表すことができる。これを変形し

$$\begin{array}{}\text{(4)}& \begin{array}{r}{i}_D=-q{D}_e{\displaystyle \frac{dn\left(x\right)}{dx}}=-q{D}_e{\displaystyle \frac{dV(x)}{dx}}{\displaystyle \frac{dn\left(x\right)}{dV\left(x\right)}}\end{array}\end{array}$$

(3)式について、$E_c(x)=q{V}_c,E_f=q{V}_f(x)$なので

$$\begin{array}{}\text{(5)}& \begin{array}{r}{i}_D=-{\displaystyle \frac{q^2{D}_e}{k_{B}T}}n(x){\displaystyle \frac{dV(x)}{dx}}\end{array}\end{array}$$

(3)ドリフト電流の式

(2)式より

$$\begin{array}{}\text{(6)}& \begin{array}{r}{i}_{\mu }=q{\mu }_{e}n(x)E\end{array}\end{array}$$

$E=-{\displaystyle \frac{dV(x)}{dx}}$をこれに代入して

$$\begin{array}{}\text{(7)}& \begin{array}{r}{i}_{\mu }=-q{\mu }_{e}n(x){\displaystyle \frac{dV(x)}{dx}}\end{array}\end{array}$$

(4)拡散電流とドリフト電流から導かれる関係式

平衡状態のとき、(5)=(7)なので

$$\begin{array}{}\text{(8)}& \begin{array}{r}{\displaystyle \frac{q{D}_e}{k_{B}T}}={\mu }_e\\ D_e={\displaystyle \frac{{\mu }_e{k}_{B}T}{q}}\end{array}\end{array}$$

これをアインシュタインの関係式と言います。

最後に

本問は、意外と院試で出題されたりします。平衡状態では、拡散電流とドリフト電流が等しいことがキーですので、与えられた文字を駆使して計算練習していきましょう。