平衡状態にある半導体を考える。伝導帯の電子密度は
\begin{aligned}n=\int ^{\infty }_{E{c}}g\left( E\right) f\left( E\right) dE\end{aligned}
で求められる。ここで、\(g(E)=4 \pi(2m_{n}/h^{2})^{3/2}(E-E_{c})\)は伝導帯の電子の単位体積当たりの状態密度、\(f(E)=[ 1+\exp { \left( E-E_{f}\right) /kT}] ^{-1}\)はフェルミディラックの分布関数であり、\(E\)は電子のエネルギー、\(m_{n}\)は電子の有効質量。\(h\)はプランク定数、\(E_{c}\)は伝導帯の底のエネルギー、\(E_{F}\)はフェルミエネルギー、\(k\)はボルツマン定数、\(T\)は温度である。
\(E>E_{c}\)において、\(E-E_{F} >> kT\)が成り立つと仮定し、以下の問いに答えよ。
(1) 式(1)を積分し、以下の式を導き、有効状態密度\(N_{c}\)を求めよ。
\begin{aligned}n=N_{c}\exp\left(-\dfrac{E_{c}-E_{F}}{kT}\right)\end{aligned}
(2)伝導帯の電子の平均エネルギーを求めよ。
東北大学 電気情報系院試 2016/3 電子工学 (1)(2)より抜粋
有効状態密度とは
ネット上では、「伝導帯の電子や正孔の密度を算出するために使用する状態密度」という簡潔な説明で溢れかえっていますが、もう少し意味を考察します。
具体的な文字は次章の解答例(1)で導出しています。ここでは物理的意味について述べます。
有効状態密度の物理的意味
式(1)を改めて見てみると、\(N_{c}\)に\(\exp\left(-\dfrac{E_{c}-E_{F}}{kT}\right)\)をかけています。
\(\exp\left(-\dfrac{E_{c}-E_{F}}{kT}\right)\)は伝導帯の底の電子の存在確率です。
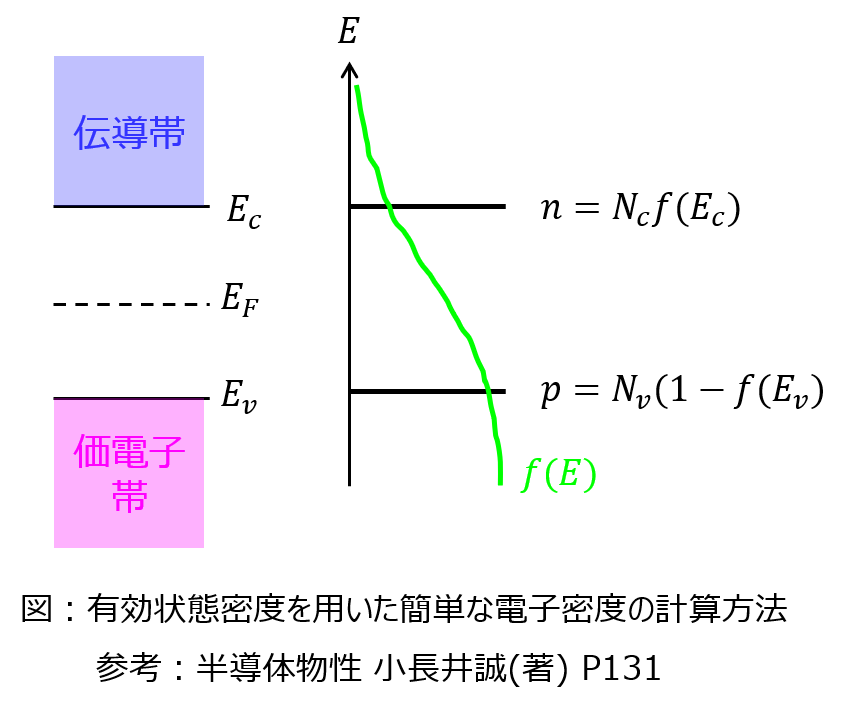
実際には、電子は伝導帯内でエネルギー的に分布しているにも関わらず、電子密度を計算するときは、下記図に示すようにあたかも伝導帯の底のみに\(N_{c}\)という状態が存在し、ここでの電子の存在確率を計算すれば良いことになる。このような意味で、”有効状態密度”とよばれる。
半導体物性 小長井誠(著) P130 より
要は、式(1)を毎回積分して電子密度を求めるわけでなく、有効状態密度に伝導帯の底のエネルギー\(E_{c}\)をexp項に使用することで、手計算で簡単に求められる。と言うわけですね。
解答例
(1)有効状態密度の導出
\begin{aligned}n=4 \pi(\dfrac{2m_{n}}{h^{2}})^\frac{3}{2}\int _{E_{c}}^{\infty }\dfrac{\left( E-E_{c}\right) ^{\frac{1}{2}}}{1+\exp \left( \dfrac{E-E_{f}}{kT}\right) }dE \end{aligned}
\(\dfrac{E-E_{c}}{kT}=x^{2}\)とすると、\(dE=kT \cdot 2xdx\)
積分範囲は、\(E:E_{c}→∞\)から\(x:0→∞\)になるので
\begin{aligned}n&=4 \pi(\dfrac{2m_{n}}{h^{2}})^\frac{3}{2}\int _{0}^{\infty } x \sqrt{kT} \exp\left(-\dfrac{E-E_{c}+E_{c}-E_{F}}{kT}\right)\cdot kT \cdot 2xdx \\ &= 4 \pi(\dfrac{2m_{n}}{h^{2}})^\frac{3}{2}(kT)^{\frac{3}{2}}\exp(\dfrac{E_{F}-E_{c}}{kT}\int _{0}^{\infty }2x^{2}\exp(-x^{2})dx\end{aligned}
ガウス積分の公式より、\(\int _{0}^{\infty }2x^{2}\exp(-x^{2})dx=\dfrac{\sqrt {\pi}}{2}\)だから
\begin{aligned}n&=4 \pi(\dfrac{2m_{n}}{h^{2}})^\frac{3}{2}(kT)^{\frac{3}{2}}\exp\left(\dfrac{E_{F}-E_{c}}{kT}\right)\dfrac{\sqrt {\pi}}{2} \\ &= 2\left( \dfrac{2\pi m_{n}kT}{h^{2}}\right) ^{\frac{3}{2}}\exp\left(\dfrac{E_{F}-E_{c}}{kT}\right)\end{aligned}
(2)式と比較して、求める有効状態密度は
\begin{aligned}N_{c}=2\left( \dfrac{2\pi m_{n}kT}{h^{2}}\right) ^{\frac{3}{2}}\end{aligned}
(2)伝導帯の電子のエネルギー
結論から言うと、ボルツマン定数を用いた運動エネルギー\(<E>=\dfrac{3}{2}kT\)になります。
下記に導出過程を示します。
単位体積内のエネルギーを持つ電子のエネルギーを全て足し、それを個数で割った値で表現できるので、下記の立式をします。
\begin{aligned}<E>=\dfrac{単位体積内(伝導帯)に存在する電子のエネルギーの総和}{単位体積内(伝導帯)に存在する電子の個数}\end{aligned}
\begin{aligned}<E>=\dfrac{\int_{E_{c}} ^{\infty }\left( E-E_{c}\right) g\left( E\right) f\left( E\right) dE}{\int_{E_{c}} ^{\infty }g\left( E\right) f\left( E\right) dE}\end{aligned}
分母は(1)で求めたので、分子を考える。
\(\dfrac{E-E_{c}}{kT}=x^{2}\)とし、(1)と同様に式変形して
\begin{aligned}(分子)=N_{c}\int_{0} ^{\infty }2x^{4}kT\exp \left( -x^{2}\right)\exp \left(\dfrac{E_{F}-E_{c}}{kT}\right)\end{aligned}
ガウス積分の公式より、\(\int_{0} ^{\infty }2x^{4}\exp \left( -x^{2}\right)=\dfrac{3}{4} \sqrt{\pi}\)だから
\begin{aligned}(分子)=\dfrac{3}{2}N_{c}kT\exp \left( \dfrac{E_{F}-E_{c}}{kT}\right)\end{aligned}
これより、式(5)と(10)の比をとり、式(8)から、求める電子の平均エネルギーは
\begin{aligned}<E>=\dfrac{3}{2}kT\end{aligned}
最後に
(1)は、院試でたまに出題されます。阪大などがそうです。
(2)は、発展的なので、導出過程というよりも答えだけ書いて部分点でも良いかもしれません。
参考文献
1.半導体物性 小長井誠(著) 有効状態密度の解説及び(1)の解答に使用
2.半導体デバイスの基礎 (上) 半導体物性 B.L. アンダーソン (著), R.L. アンダーソン (著), 樺沢 宇紀 (翻訳) (2)の解答作成に使用