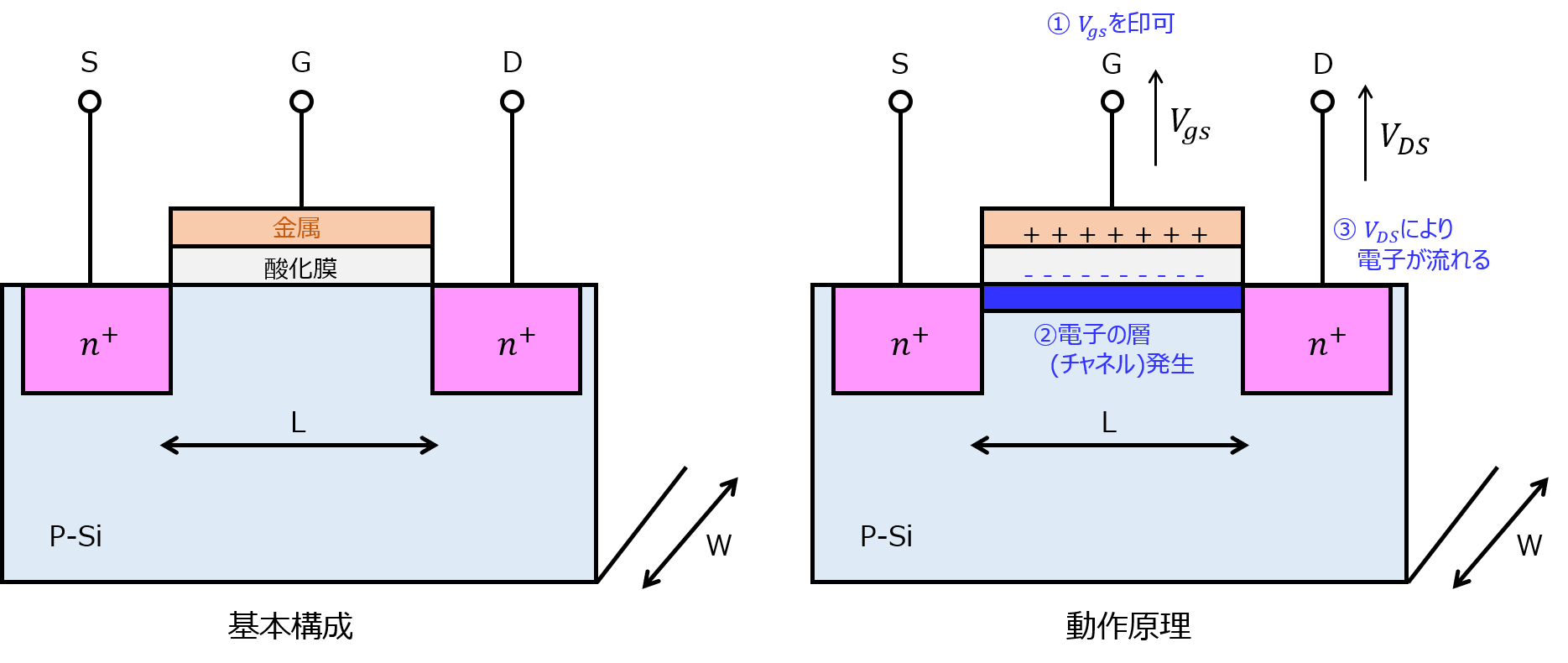
下記のように、チャネル長\(L\)、ゲート幅\(L\)のMOSFETを考える。ゲート電圧\(V_{gs}\)及びドレイン-ソース間電圧\(V_{DS}\)を印可する。印可の大きさにより、ドレイン-ソース間に流れる電流値\(I_{DS}\)が3通り変化する。それぞれの場合の\(I_{DS}\)の式を導出し、相互コンダクタンス\(g_{m}\)も計算せよ。
なお、閾値電圧を\(V_{th}\)酸化膜の静電容量を\(C_{ox}\)、電子移動度を一定値\(\mu\)とする。(定移動度モデル)
はじめに
本問は、半導体デバイスを院試範囲とする大学で頻出となっています。東大、阪大、東北大、九大、北大、農工大など多くの大学が対象になります。
一般的に電流は、電荷量\(e\),電荷密度\(n\),速度\(v\),面積\(S\)を用いて、\(I=envS\)と表すことができます。
この式をベースに、MOSFET(電界効果トランジスタ)で発生するドレイン電流値\(I_{DS}\)を導出します。
是非、何も見ずに導出できるようになることをオススメします。
本問で覚えたいこと
全体方針
ある地点\(x\)で流れる電流値を算出し、これをチャネル幅\(L\)の範囲で積分することでドレイン電流\(I_{DS}\)を算出します。
下記1~4が積分するための式を立式する段階です。
5は、積分結果を印可電圧\(V_{gs},V_{DS}\)によって場合分けし、条件ごとに流れる\(I_{DS}\)を求めます。
- ある地点xにおける電流\(I_{DS}=envS\)をMOSFETのパラメータに置き換えていく
- \(en=\dfrac{dQ_{x}}{dx}=\dfrac{C_{ox}(V_{GS}-V_{th}-V_{x})}{dx}\)で置き換える。(\(V_{x}\)はある地点の電位)
- \(v=\mu E=\mu \dfrac{dV_{x}}{dx}\)で置き換える(\(E\)は電場)
- \(S=W\)で置き換え、下記の式を導出する。
\begin{align}&I_{DS}dx=\mu W C_{ox}(V_{gs}-V_{th}-V_{x})dV_{x}\end{align} - \(0≦x≦L , 0≦V_{x}≦V_{DS} \) の範囲で積分し、\(I_{DS}\)の式を求める。
(i)\(V_{gs}≧V_{th} \) かつ \( V_{DS}≦V_{gs}-V_{th}\) のとき、抵抗性領域であり、積分値がそのまま答えになる
(ii)\(V_{gs}≧V_{th} \) かつ \( V_{DS}≧V_{gs}-V_{th}\) のとき、定電流領域であり、\(V_{DS}=V_{gs}-V_{th}\)を代入した値が求める電流値になる。
(iii)\(V_{gs}≦V_{th}\) のとき、遮断領域であり反転層が形成されない。そもそも電流が流れない。\(I_{DS}=0\) - \(g_{m}=\dfrac{dI_{D}}{dV_{gs}}\)より、相互コンダクタンスを求める。
解答例で実際に説明を、、としたいところですが、その前にMOSFETの基本的な動作原理を説明します。
MOSFETの動作原理
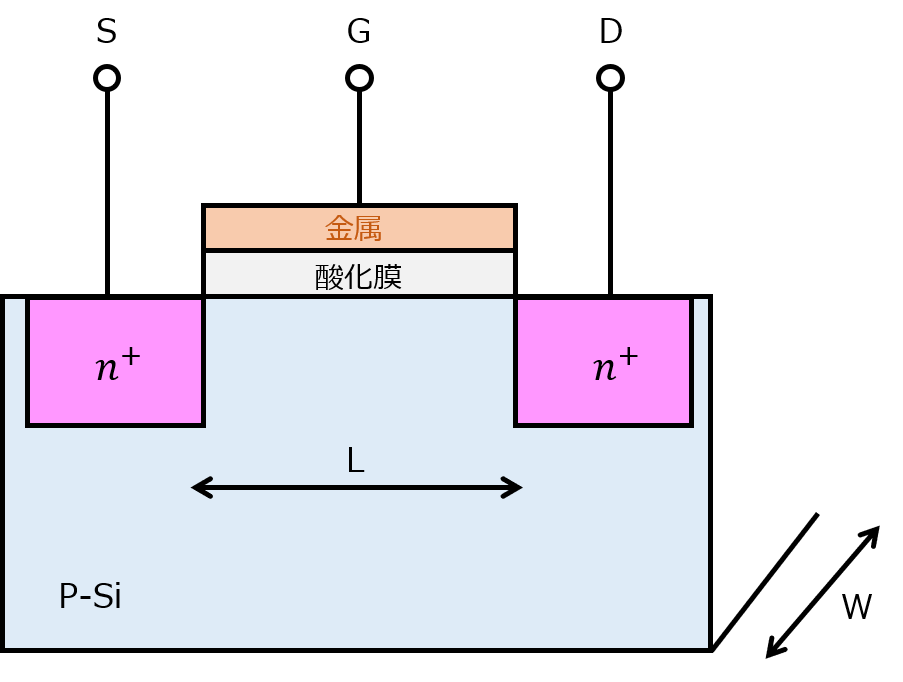
ゲート及びドレインに電圧をかけることで、ドレイン-ソース間に電流を流すことができるスイッチング素子です。下記のような構成となっており、ゲートと基盤の間に薄い絶縁体(酸化膜)が挟まっています。
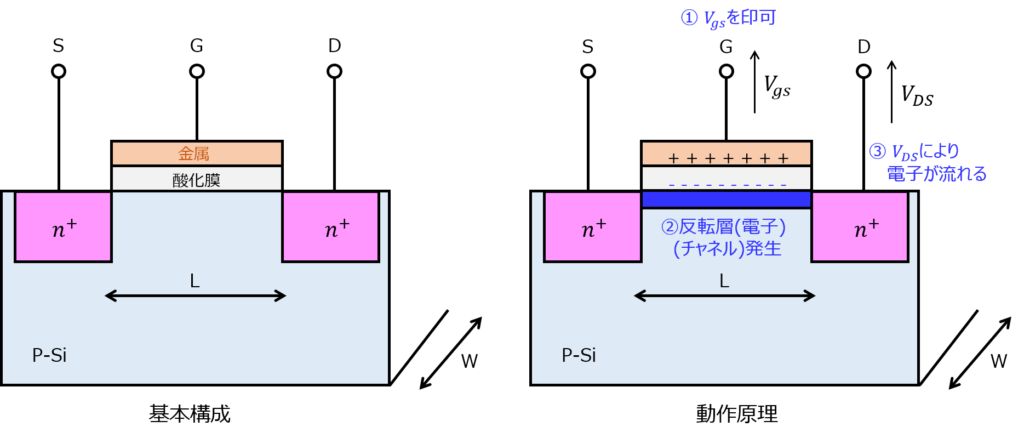
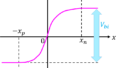
ゲートに印可する電圧\(V_{gs}\)を上昇したときの動作をエネルギーバンド図を用いて考えます。
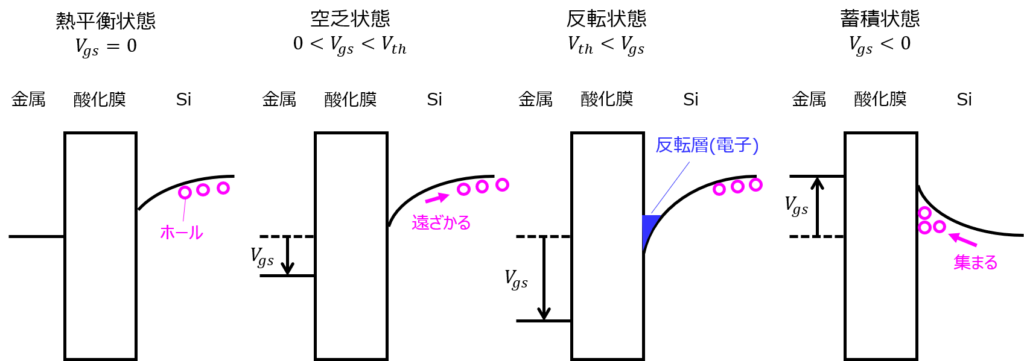
\(V_{gs}=0\)のとき、酸化膜界面には電荷が発生しません。
ここで、徐々に電圧を上げていくと、電場が発生します。このとき、基盤に存在するホールが遠ざかる振る舞いになります。これを「空乏」と言います。
さらに電圧をあげると、酸化膜と基盤の境界面付近に電子が誘起します。これを「反転」と言います。反転状態にあるとき、ドレイン-ソース間に電子が通る道(チャネル)が発生するため、ドレイン-ソース間に電圧をかけると電流が流れるようになります。まさに、本問で考える状態です。反転が発生するときの閾値電圧は、\(V_{th}\)で表されることが多いです。
なお、ゲートに負の電圧を加えると、境界面にはホール(正孔)が集まります。これを「蓄積」と言いますが、本問では取り扱いません。
解答例
積分対象の式\(I_{DS}=\)を立てる
1.については、冒頭で説明したように、定義通りです。
2.については、ある地点xからx+dxにおける微小電荷密度を表しています。微小区間dxにおける電荷は一定値とみなせるため、\(Q=CV\)の式から導出できます。
3.については、半導体デバイスの分野で良く出てくる式です。電場を印可すると電子は移動しますが、半導体の種類によって動きやすさは変化します。これを電荷移動度\(\mu\)で表し、結果\(v=\mu E\)とします。
4.についてはそのままです。
\begin{cases}I=enuS\\ en=\dfrac{dQx}{dx}=C_{ox}\times \left( V_{gs}-V_{th}-V_{x}\right) \\ v=-\mu E=\dfrac{dV_{x}}{dx}\\ S=W\end{cases}
{ の第一式に二式以降の値を代入することで、(1)式を導出できます。
\(0≦x≦L , 0≦V_{x}≦V_{DS} \) の範囲で積分し、\(I_{DS}\) の式を求める。
(1)式を本節で提示した範囲で積分する。
\begin{align} \int ^{L}_{0} I_{D}dx &= \mu W C_{ox}\int ^{V _{DS}}_{0} \left( V_{gs}-V_{th}-V_{x}\right) dV_{x} \\ I_{DS} L &= \mu W C_{ox} \left( (V_{gs}-V_{th})V_{DS} – \dfrac{V_{DS}^{2}}{2} \right) \end{align}
ここから、印可電圧による条件分けをします。
(i)\(V_{gs}≧V_{th} \) かつ \(V_{DS}≦V_{gs}-V_{th}\) のとき
このときは、\(V_{DS}\)がまだ小さい領域です。(線形領域)
\(V_{DS}\)をかけた分だけ電場が強まり、ドレイン電流\(I_{DS}\)が上昇します。(4)式を用いて、\(I_{DS}\)は以下で表せます。
\begin{align}I_{DS} &= \dfrac{\mu W C_{ox}}{L} \left( (V_{gs} – V_{th})V_{DS} – \dfrac{V_{DS}^{2}}{2} \right) \end{align}
この時の相互コンダクタンスは
\begin{align} g_{m}=\dfrac{dI_{D}}{dV_{gs}} = \dfrac{\mu W C_{ox} V_{DS}}{L} \end{align}
(ii)\(V_{gs}≧V_{th} \) かつ \(V_{DS}≧V_{gs}-V_{th}\) のとき
\(V_{DS}\)を大きくすると、ドレイン周りの空乏層が大きくなります。この結果、反転層がドレインに到達せず、反転層が途中で途切れることになります。(ピンチオフ点と言います。)
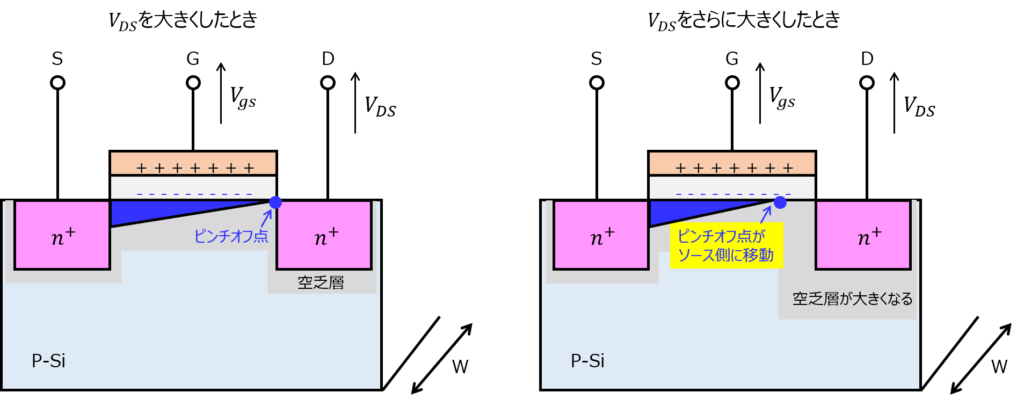
これ以上電圧をかけても、チャネルはソース側に偏り、短くなるのみです。ドレイン電流は上昇しなくなります。これを定電流領域(または飽和領域)と言います。
\(I_{DS}\)は、(5)式に\(V_{DS}=V_{gs}-V_{th}\)を代入し
\begin{align}I_{DS}=\dfrac{\mu C_{ox} W}{2L}\left( V_{gs}-V_{th}\right) ^{2}\end{align}
で表すことができます。相互コンダクタンスは、(i)と同様の計算を行い
\begin{align}g_{m}=\dfrac{\mu C_{0} W}{L}\left( V_{gs}-V_{th}\right)\end{align}
になります。
(iii)\(V_{gs}≦V_{th}\) のとき
そもそも反転層が形成されないので電流は流れない。\(I_{DS}=0 , g_{m}=0\)
MOSFETの特性
前節(i)~(iii)の結果から、\(V_{gs},V_{DS},I_{DS}\)の関係は以下のようになります。
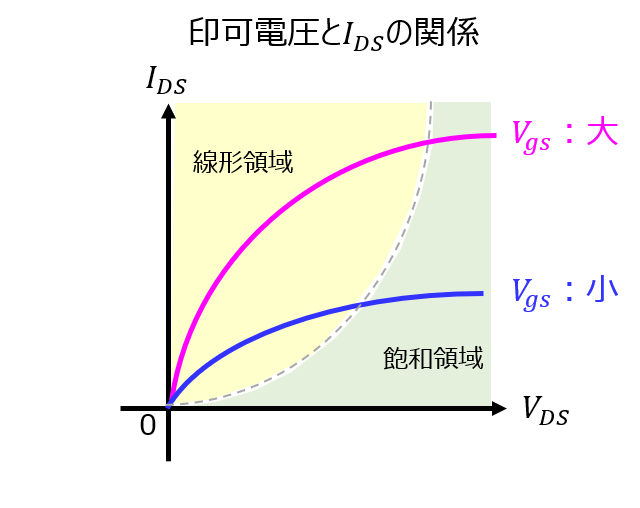
ゲート電圧をかけるほど、反転層が大きくなるので電流は大きくなります。ただし、(ii)の条件を満たし次第、いかなる\(V_{gs}\)の場合でも定電流領域に移行します。
ここまで覚えていると、院試で大分得点できるようになると思います。
しかし、満点を取る場合だと追加で押さえておきたい内容があります。これを次章に示します。
発展:実際のドレイン電流値は理論値通りに流れない
前章までで算出したドレイン電流は、あくまでも電子移動度が一定(理想的)の場合です。
実際は、様々な要因により、理論値通りの\(I_{DS}\)が流れないことがあります。本章では、代表的な事象を3つ紹介します。
チャネル長変調効果 \(V_{DS}\)起因
前章(ii)では、ピンチオフ点を境に、チャネル長が短くなっていくと説明しました。理想的には定電流になりますが、本当にそうなのでしょうか。
実際は、チャネル長が短くなったことにより、Lの値が小さくなります。
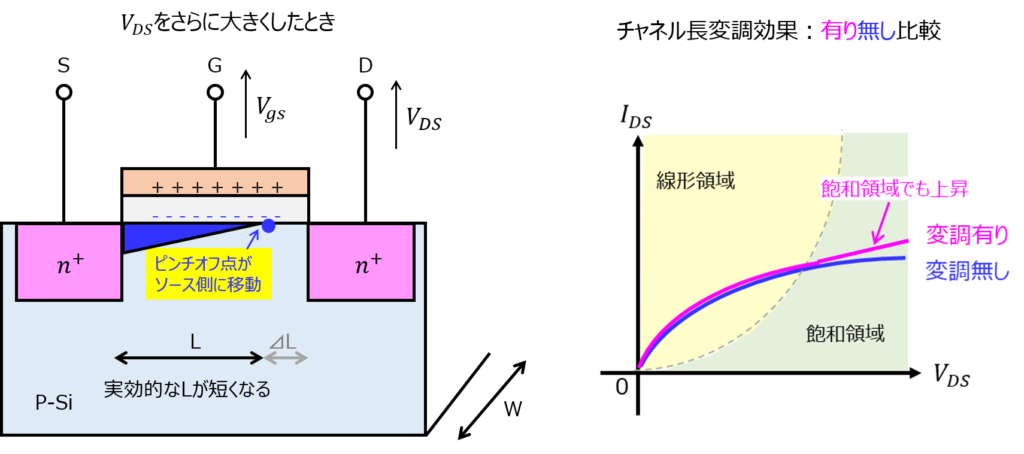
これを(5)式に代入すると、分母が小さくなるので、ドレイン電流が大きくなることが分かります。
このように、定電流領域であっても、ドレイン-ソース電圧を大きくするとドレイン電流\(I_{DS}\)は大きくなることが分かりました。これをチャネル長変調効果と言います。
北大、神戸大で問われたことがありますので、両大学を志望される方は是非抑えてください。
光学フォノン散乱による電子速度の飽和 \(V_{DS}\)起因
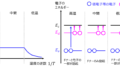
式(2) 第3式により、電子速度は\(v=\mu E\)と表せます。よって、この式だけを見ると、\(V_{DS}\)を印可するほど\(E\)が上昇し、電子速度が上昇する=電流値も上昇する。と考えられます。しかし、実際はどこかで飽和します。
理由は、光学フォノン散乱によるものです。

上記の図のように、電子は衝突断面積を持って動きます。電場が大きくなると、単位時間辺りに進む距離が長くなり、フォノンとの衝突から次の衝突までの平均衝突時間が短くなります。この結果、電場を大きくしても電子移動度はあまり大きくならず、いずれ飽和します。
傾斜ポテンシャルによる電子移動度低下 \(V_{gs}\)起因
ゲート電圧要因でも、電子移動度は低下します。理由は、傾斜ポテンシャルにより、ドレイン-ソースに対して垂直方向にも電場がかかるからです。
既に説明した通り、バンド図で、反転状態になると反転層が現れます。このとき、基盤側のバンドは大きく傾斜しています。この結果、垂直方向に電場がかかり、電子はドレインに対しまっすぐ進まなくなります。電子は、側壁との衝突、散乱を繰り返しドレインに到達しますので、電子移動度は低下します。
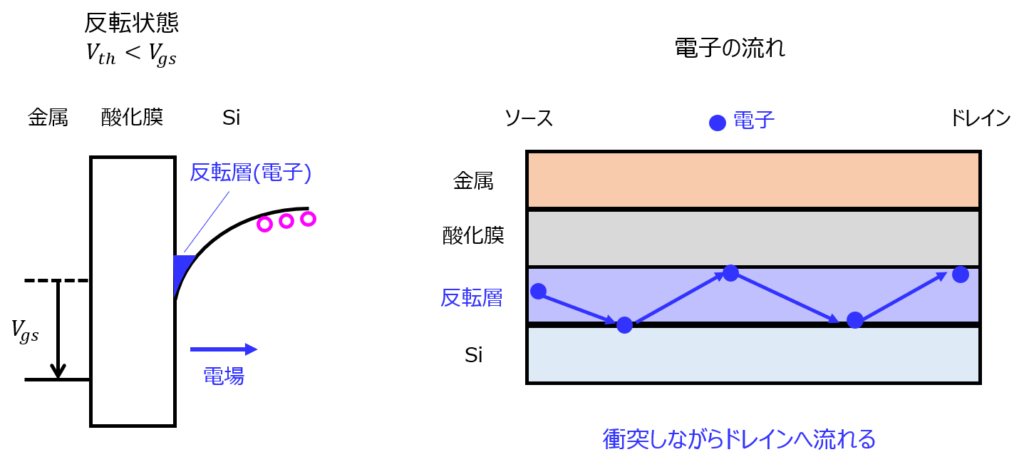
ゲート電圧\(V_{gs}\)を大きくすると、傾斜ポテンシャルは大きくなりますので、この影響は大きくなります。
最後に
酸化膜の静電容量\(C_{ox}\)は、誘電率\(ε_{ox}\),酸化膜の厚み\(t_{ox}\),酸化膜の面積\(S_{ox}\)を利用し、\(C_{ox}=\dfrac{ε_{ox}S_{ox}}{t_{ox}}\)で表すこともあります。
各々の条件におけるドレイン電流の式は、結果だけ載せているサイトが多かったです。業務だとそれで良いかもしれませんが、院試だと一からの導出を求められることが多いです。
原理原則からの理解に、本記事がお役に立てると幸いです。
参考文献
電子情報回路Ⅰ:樋口 龍雄(著) P33
半導体デバイスの基礎(中) <ダイオードと電界効果トランジスタ>:B.L.アンダーソン(著),R.L.アンダーソン(著) 樺沢 宇紀(訳) 第7章