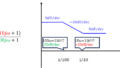
次の方程式により表現される制御系を考える。ただし、この制御系のブロック図は図1に与えられるものとする。
\begin{cases}e\left( t\right) =t\left( t\right) -y\left( t\right) \\ A\dfrac{dp}{dt}+\rho \left( t\right) =ke\left( t\right) \\ q\left( t\right) =\rho \left( t\right) +d\left( t\right) \\ B\dfrac{d}{dt}\left( \dfrac{dy}{dt}\right) +\dfrac{dy}{dt}=q\left( t\right) \end{cases}
変数r(t),y(t),e(t),p(t),d(t)はそれぞれこの制御系の目標値、制御量、偏差、ブロック\(G_{1}\)の出力、外乱である。定数\(A,B,K\)は正の定数である。このとき、以下の問いに答えよ。
(1) 式(1)をラプラス変換し、図1の\(G_{1}(s),G_{2}(s)\)を求めよ。ただし、\(y(0)=0,y'(0)=0\)とせよ。
(2)r(t)=0とする。偏差\(E(s)\)を\(G_{1}(s),G_{2}(s),D(s)\)を用いて表せ。その結果を用いて、外乱\(d(t)\)が単位ステップ関数で与えられるときの定常偏差\(\varepsilon _{d}\)を求めよ。
東北大学 電気情報系院試 2007年8月 電気工学から一部抜粋

はじめに
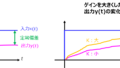
本問は、前回の記事の続きです。今まで、入力に対する出力の定常偏差について説明してきましたが、本問は、外乱による定常偏差を考えます。
外乱は、入力とは別にシステムの途中から入力される量です。図1が分かりやすいです。その名の通り、入力に対する出力が外乱によってずれますので、これも勘案したシステム設計が必要です。
また、今まで紹介してきた問題は、伝達関数が予め与えられた状態で議論してきましたが、本問では微分方程式から始まります。
これを伝達関数に落とし込むところから始めますが、方針としてはシンプルです。入力に対する出力の比を取るように式を変形。未知数を削除していくのみです。
解答例
(1)微分方程式からの伝達関数の導出
式(1)をラプラス変換すると、以下のようになる
\begin{cases}E\left( s\right) =R\left( s\right) -Y\left( s\right) \\ sAP\left( s\right) +p\left( s\right) =KE\left( s\right) \\ Q\left( s\right) =P\left( s\right) +D\left( s\right) \\ s^{2}BY\left( s\right) +sY\left( s\right) =Q\left( s\right) \end{cases}
ブロック線図より、
\begin{eqnarray}P(s)=G_{1}(s)Q(s)\end{eqnarray}
なので、第二式と比較して
\begin{eqnarray}P\left( s\right) =\dfrac{K}{sA+1}E\left( s\right)\end{eqnarray}
\begin{eqnarray}G_{1}(s)=\dfrac{K}{sA+1}\end{eqnarray}
また、
\begin{aligned}Y\left( s\right) =G_{2}\left( s\right) Q\left( s\right) \\ =\dfrac{1}{s\left( sB+1\right) }Q\left( s\right) \end{aligned}
\begin{eqnarray}G_{2}(s)=\dfrac{1}{s\left( sB+1\right) }\end{eqnarray}
(2)外乱による定常偏差
偏差\(E(s)=R(s)-Y(s)\)で、\(R(s)=0\)より
\begin{eqnarray}E(s)=-Y(s)\end{eqnarray}
外乱分による出力は下記で表すことができる。
\begin{aligned}Y\left( s\right) =-G_{1}G_{2}Y(s)+G_{2}D\left( s\right)\end{aligned}
これを変形し、
\begin{aligned}Y(s)&=-\dfrac{G_{2}(s)}{1+G_{1}(s)G_{2}(s)}D(s) \\ &= -\dfrac{sA+1}{s\left( sA+1\right) \left( sB+1\right) +K}D(s) \end{aligned}
\(D(s)=\dfrac{1}{s}\)と最終値の定理から、求める定常偏差は
\begin{aligned}\varepsilon _{d}&=\lim _{s→0}-s\dfrac{sA+1}{s\left( sA+1\right) \left( sB+1\right) K}\cdot \dfrac{1}{s} \\ &=-\dfrac{1}{K}\end{aligned}
最後に
本問は、(9)式を立てられるかが肝です。これさえできれば、後は式(8)に代入し、最終値の定理から結果が求まります。