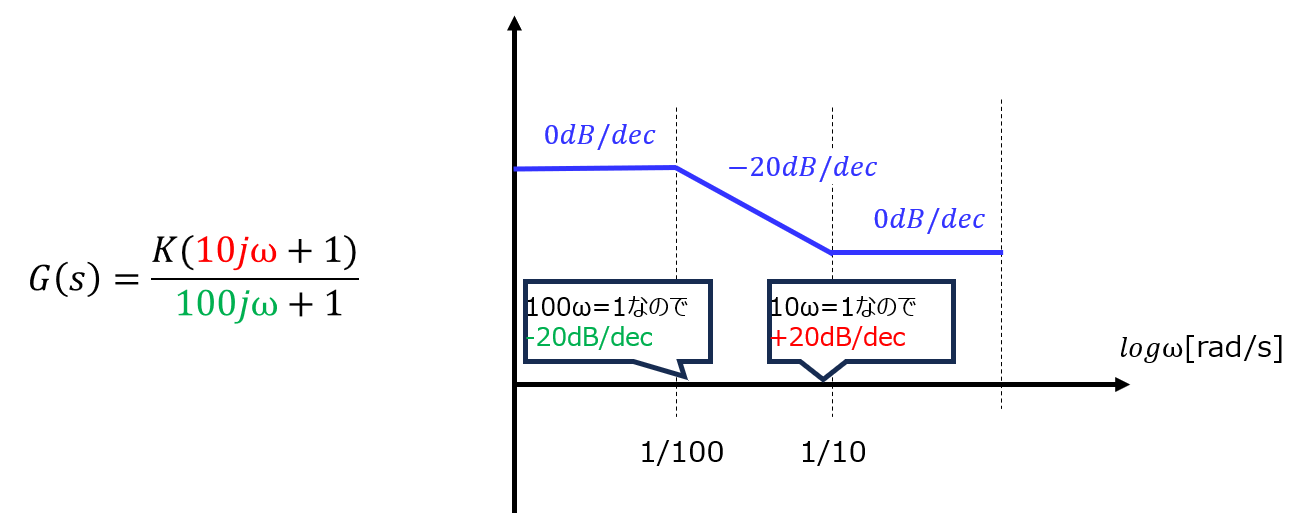
(1)図1の制御系の閉ループ伝達関数\(G_{0}(s)\)を求めよ。
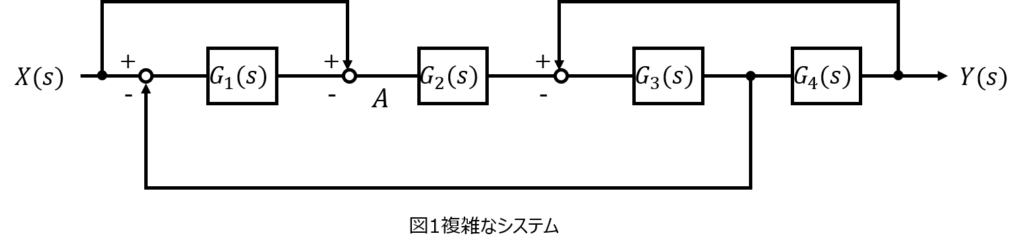
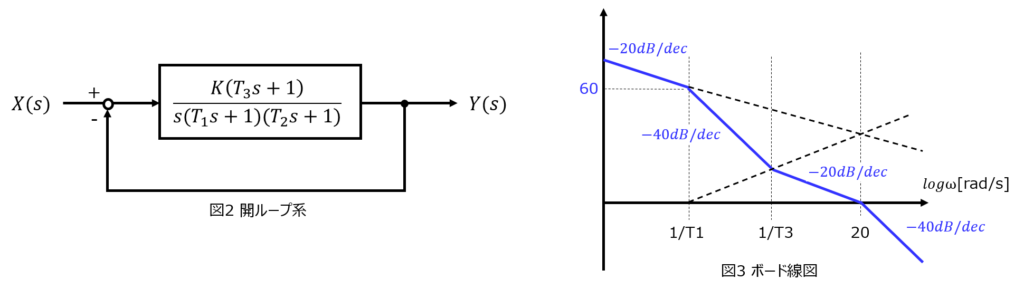
(2)図1の制御系が、図2の開ループ系に簡単化できるとする。ボード線図が図3で与えられるとき、\(K,T_{1},T_{2},T_{3}\)を求めよ。
はじめに
複雑な伝達関数を簡単化する問題は、意外と院試で出題されます。(1)で結果を求め、その結果で(2)以降に続いていく段取りです。
本問も、それを意識して作りました。ボード線図を読み解く問題も頻出ですので、一緒に確認できればと思います。
解法の方針
伝達関数の簡単化
至ってシンプルです。与えられたブロック図の内容を数式に落とし込み、入力と出力の比を取る原則に従います。
ボード線図の読み方
伝達関数の分母分子に注目します。
括弧内を\(1+As\)形にして、周波数領域\(1+Aj\omega \)に変換します。
ωを大きくしていき、\(A\omega=1\)になったとき、分子ならば\(+20dB/dec\)、分母ならば\(-20dB/dec\)傾きを変化させます。
下記の図で例を示します。
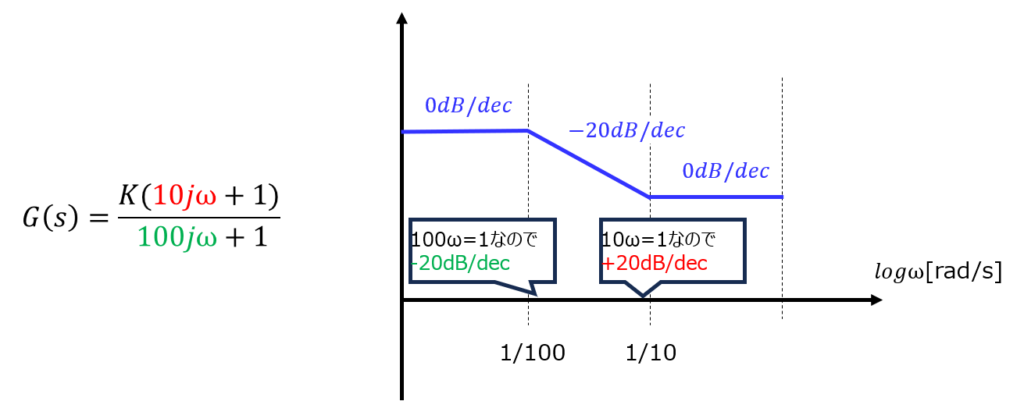
括弧が一次の項ならば\(+-20dB/dec\)ですが、2次ならば\(+-40dB/dec\)です。次数にも注目しましょう。
解答例
(1)伝達関数の簡単化
\begin{cases}A=G_{1}\left( X+\dfrac{Y}{G_{4}}\right) -H_{1}R\\ Y=\left( AG_{2}-YH_{2}\right) G_{3}G_{4}\end{cases}
第2式より
\begin{eqnarray}\left( 1+H_{2}G_{3}G_{4}\right) Y=G_{2}G_{3}G_{4}A\end{eqnarray}
第1式をこれに代入して
\begin{aligned}\left( 1+H_{2}G_{3}G_{4}\right) Y&=G_{1}G_{2}G_{3}G_{4}\left( R+\dfrac{y}{G_{4}}\right) +H_{1}G_{2}G_{3}G_{t}R \\ G\left( s\right) &=\dfrac{Y}{R}= \dfrac{G_{2}G_{1}G_{4}\left( G_{1}+H_{1}\right) }{1+H_{2}G_{3}G_{4}-G_{1}G_{2}G_{3}}\end{aligned}
(2)ボード線図の読み方
\begin{eqnarray}G\left( j\omega \right) =\dfrac{K\left( 1+j\omega T_{3}\right) }{j\omega \left( 1+i\omega T_{1}\right) \left( 1+j\omega T_{2}\right) }\end{eqnarray}
\(\omega=20\)で-20dB/dec傾きが急になるので、
\begin{eqnarray}\dfrac{1}{T_{2}}=20 ⇔ T_{2}=0.05\end{eqnarray}
\(\omega=\dfrac{1}{T_{1}}\)で60dBなので、
\begin{eqnarray}20log|KT_{1}|=60 ⇔ KT_{1}=10^{3}\end{eqnarray}
伝達関数のゲインは
\begin{aligned}20\log \left| \dfrac{k}{\omega }\right| +20\log \left| \omega T_{3}\right| -20\log \left| \omega T_{1}\right| -20\lg \left| \omega T_{2}\right|=0 \end{aligned}
と表すことができ、\(\omega=20\)のとき0になるので
\begin{eqnarray}\dfrac{kT_{3}}{T_{1}T_{2}}=\omega ^{2} \\ \dfrac{kT_{3}}{T_{1}T_{2}}=400\end{eqnarray}
また、\(\omega=20\)のとき\((1+sT_{3})\)と\(\frac{K}{s}\)成分のゲインが等しいので
\begin{eqnarray}20\log \left| \omega T_{3}\right| =20\log \left| \dfrac{k}{\omega }\right| \\ 20T_{3}=\dfrac{K}{20}\end{eqnarray}
\begin{aligned} k=400T_{3} \end{aligned}
(5)(6)(9)(12)式を用いて具体的な値を求めていく
(9)より、\(\dfrac{1}{20}\cdot \dfrac{k}{T_{1}}\cdot T_{3}=400\)
(6)(12)を代入して
\begin{aligned}20\cdot \dfrac{K^{2}}{10^{3}},\dfrac{K}{400}=400\\ k^{3}=8.0\times 10^{6}\\ K=200\end{aligned}
(12)より、
\begin{eqnarray}T_{3}=0.5\end{eqnarray}
(9)より、
\begin{aligned}T_{1}&=\dfrac{1}{400}\cdot \dfrac{KT_{3}}{T_{2}}\\ &=5\end{aligned}
最後に
ボード線図の読み解きは、特に九大で出題されます。同大学を志望される方は、是非本問で練習すると良いです。