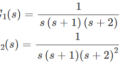【問】以下3つの安定性判別方法は、全て数学的に等価であることを説明せよ。ただし、例として開ループ伝達関数\(G(s)=\dfrac{1}{(s+1)(s+3)}\)を使用して良い。
・閉ループ伝達関数の極が全て負
・ラウス・フルビッツの安定判別法
・ナイキストの安定判別法
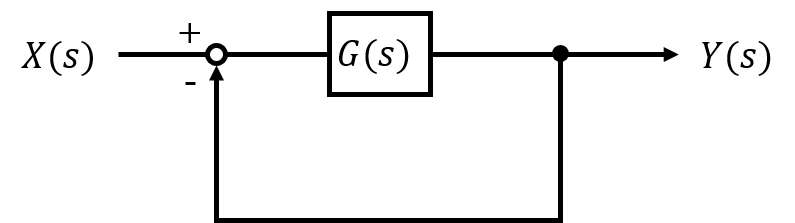
はじめに
制御の試験問題は、教科書や問題集で掲載されているものとあまり変わらない印象です。ですので、自学自習は比較的行いやすい分野のはずです。
そこで、本記事では趣向を変えます。標記の問題の安定判別法はどの本でも当たり前のように使っていますが、そもそもの意味について考えることにします。(頻出問題については次回以降の記事で紹介)
古典制御の安定判別法とその意味
代表的な項目として、以下3つの安定判別法があります。
- 閉ループ伝達関数の極が全て負
- ラウス・フルビッツの安定判別法(特性方程式 \(1+G(s)=0\)が安定条件を満たす)
- ナイキストの安定判別法 (一巡伝達関数のベクトル線図が(-1,j0)を左に見る)
それぞれ対象の伝達関数が異なるため、考え方の背景から異なるように見えます。しかし、実際は全て同じ背景(閉ループ伝達関数の極が全て負)から発する安定判別法であることを示します。
閉ループ伝達関数の極が全て負 ⇒ 安定である理由
こちらについてはシンプルです。
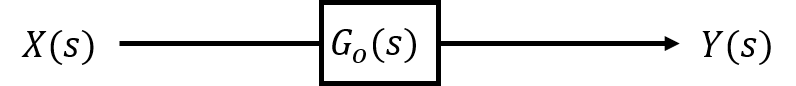
ある閉ループ伝達関数\(G_{o}(s)\)が与えられているとき、出力\(Y(s)\)は、入力\(X(s)\)を用いて以下のようになります。
\begin{eqnarray}Y(s)=G_{o}(s)X(s)\end{eqnarray}
本問で与えられた開ループ伝達関数ならば、\(G_{o}(s)=\dfrac{G_{s}}{1+G_{s}}=\dfrac{1}{s^{2}+4s+4}\)になります。
簡単化のため、入力\(x(t)\)には、単位インパルス関数\(X(s)=1\)を与えたとします。
この時、安定性を決めるのは閉ループ伝達関数\(G_{o}(s)\)の性質です。
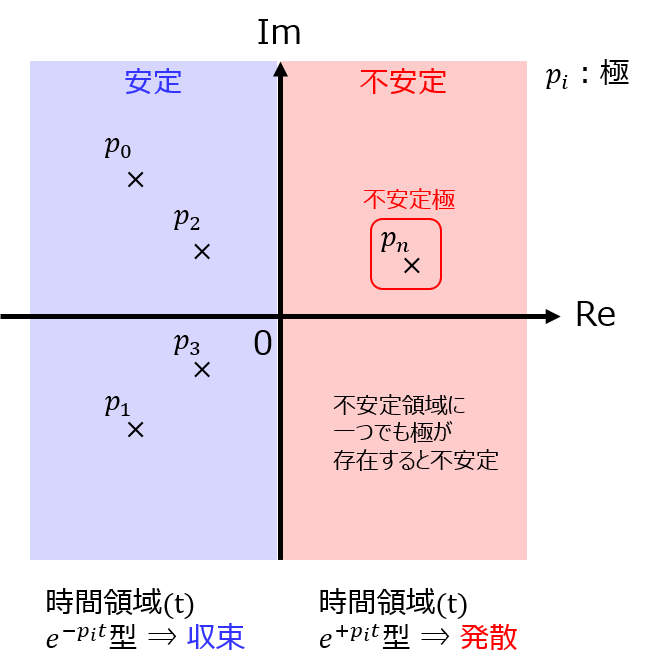
分母の極が全て負ならば、ラプラス逆変換したとき、出力\(y(t)\)のexp項は全て\(e^{-at}\)型になる。
(本問の場合は、\(s^{2}+4s+4=(s+2)^{2}\) より、\(e^{-2t}\) 型)
よって、t→∞の極限を考えたとき、一定値に収束。安定である。
ラウス・フルビッツの安定判別法
開ループ伝達関数\(G(s)=\dfrac{1}{(s+1)(s+3)}\)に対して、特性方程式\(1+G(s)=0\)を考える。
\begin{eqnarray}1+G(s)= 0 \\ s^2+4s+4=0 \end{eqnarray} 以下の安定条件を満たせば良い。
- 係数が全て正
- 行列\begin{vmatrix} 1 & 4 \\ 0 & 4\end{vmatrix}が0より大きい
結果:(3)式より、係数は全て正。行列の演算結果は、4>0。両方満たすので安定である。
問題を解くうえでは上記までで良いです。しかし、この特性方程式、どこかで見たことはありませんか。
正解は、前節で説明した閉ループ伝達関数の根と一致しています。
「安定判別条件」と難しいことを覚えているように見えますが、結局は閉ループ伝達関数の極が全て負であることを特定のルールに基づいて考えているに過ぎませんでした。
今回は計算しやすい形だったので、こちらの方法を使わなくとも前節(極の配置)で直接安定判別できました。
しかし、複雑な根になるにつれて、手計算で直接極を求めることは困難になってきます。こういった時に、極の具体的な位置が分からずとも、符号さえ分かれば良いと考える制御工学において非常に有用なものとなります。
ナイキストの安定判別法
安定判別方法:一巡伝達関数のベクトル軌跡が(-1,j0)を左に見るとき、与えられたシステムは安定である。
ひっかけ問題として、閉ループ伝達関数のベクトル軌跡を書かせるよう受験者に仕向けることが多い安定判別方法ですが、こちらも「閉ループ伝達関数の極が全て負」を起点とした安定判別条件です。(※あくまでも考え方の話で、実際に問題を解くうえで使用するのは一巡伝達関数です。絶対に間違えないでください。)
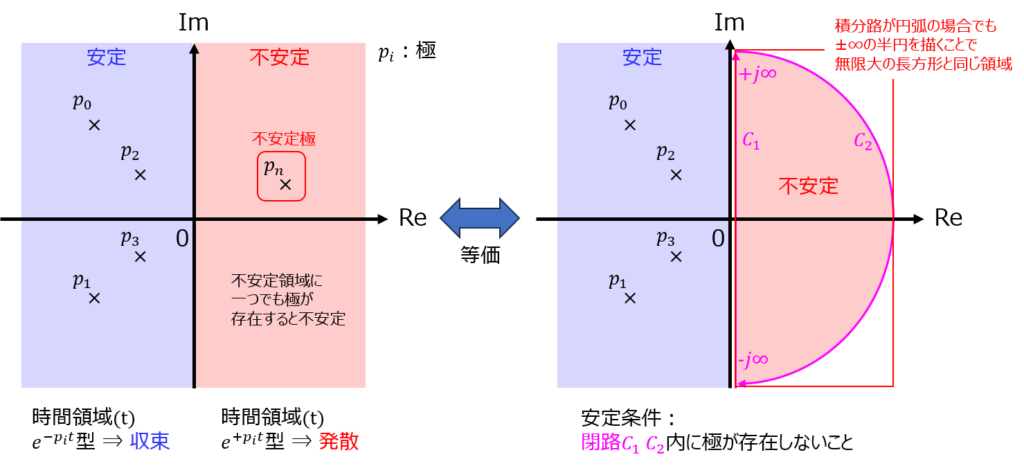
まずは、閉ループ伝達関数の極が負である ⇒ 安定 である理由を別の視点から考えてみましょう。その一つとして、上図のようにs平面の右半面に無限大の半円を取る閉路\(C_{1},C_{2}\)を考え、その閉路内に極が無いこと。と言い換えられます。
このままでは元々の条件とあまり変わりませんので座標変換を考えます。極配置を表す特性方程式\(1+G(s)=0\)を変形し、\(G(s)=-1\)とします。
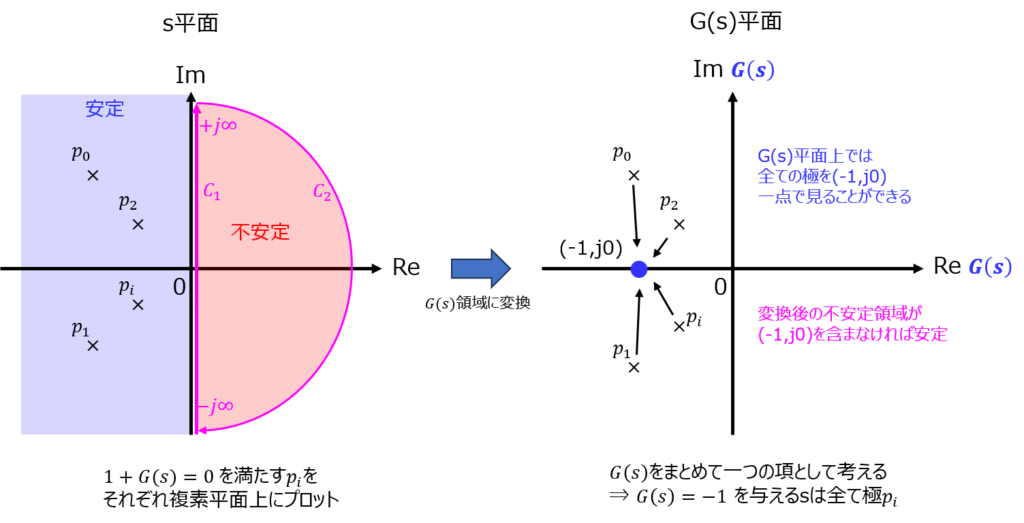
元々は\(G(s)=-1\)を与える極を精査し、条件を満たすそれぞれの極の位置を「s平面上(左図)」で考えていました。しかし、式の見方を変えて、\(G(s)\)を一つの項(固まり)として捉え、\(G(s)\)の実部、虚部をプロットする「\(G(s)\)-平面(右図)」を考えるようにします。(座標変換)
座標変換すると動くのは、1.極の位置 と 2.閉路\(C_{1},C_{2}\)の領域です。
1.極の配置について:\(G(s)\)平面上では、\(1+G(s)=0\)の極は全て点(-1,j0)に集まります。(理由:どの極も\(G(s)=-1\)を満たすため。)
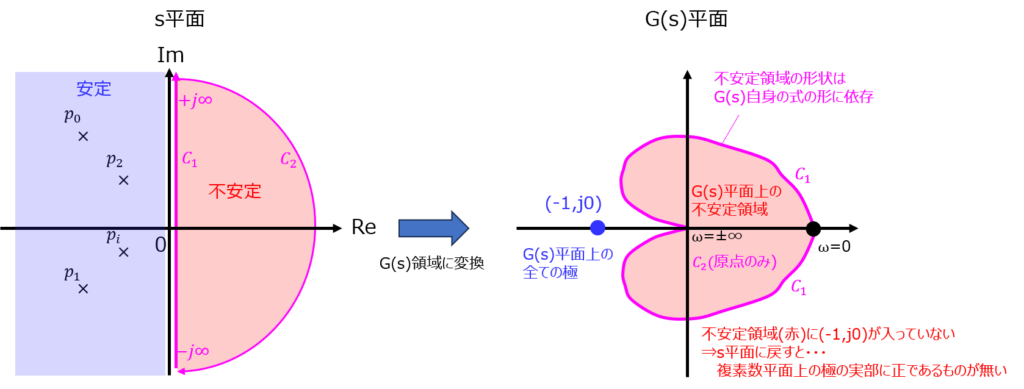
2.閉路\(C_{1}、C_{2}\)について:線路\(C_{2}\)は\(s=∞exp(j∞)\)の無限円弧である。開ループ伝達関数の次数は、一般的に分母の次数の方が大きいので、線路\(C_{2}\)上では\(G(∞)=0\)。よって、\(C_{1}\)の線路が\(G(s)\)平面上の軌跡にあたり、終点は必ず原点(0,0)になることが分かった。\(ω\)が負のときの軌跡も踏まえると、\(C_{1}\)の軌跡で閉路が出来上がり、この内部が不安定領域である。
つまり、与えられた開ループ伝達関数\(G(s)\)を、s平面ではなく\(G(s)\)平面で考えると、閉ループ伝達関数に変換したときの全ての極を(-1,j0)で固定することが可能。閉路が囲む領域のみで安定性の判別ができるようになりました。
開ループ伝達関数(一巡伝達関数)\(G(s)\)の状態で安定性を考えることができるようになったため、他の安定性判別方法のように、閉ループ伝達関数を求める必要が無くなりました。
閉ループの極配置から始まった今回の安定性判別議論も、座標変換を工夫することで開ループのまま判別することができるようになったのでした。
上記で冒頭の問について回答完了ですが、折角なので、本問で与えられた開ループ伝達関数\(G(s)=\dfrac{1}{(s+1)(s+3)}\)のナイキスト線図をプロットしてみます。
\(ω=0\)のとき、\(G(0)=1/3\) で、\(ω→∞\)のとき、\(G(∞)=0\)
\(G(jω)\)の位相は、\(-\tan^{-1}(ω)-\tan^{-1}\dfrac{ω}{3}\)なので、以下のようになる。
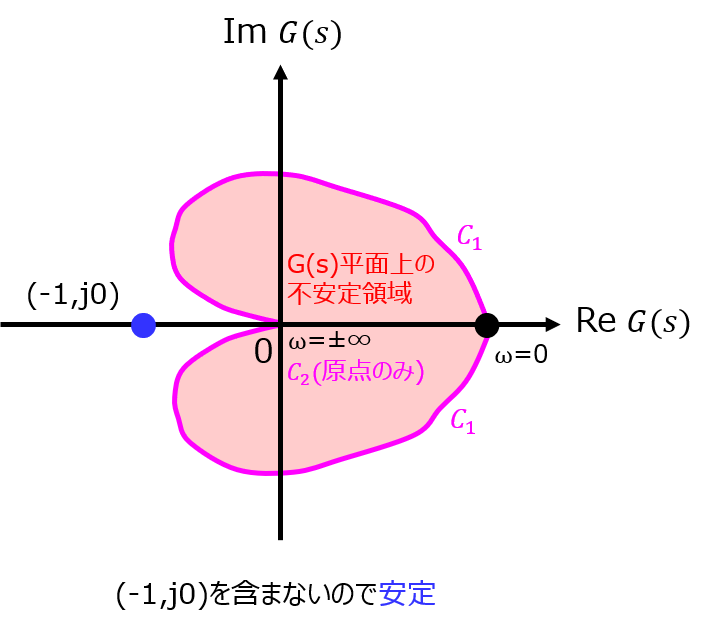
不安定領域が(-1,j0)を含まないので、確かに安定であることが示されました。
問題集では、「(-1,j0)を左に見るので安定」とよく表現されています。この記載でも合っているはずですが、厳密に記載するならば、「ベクトル軌跡の不安定領域が(-1,j0)を含まないので安定」とした方が良いかもしれません。
ナイキスト線図に一巡伝達関数を使用する理由
冒頭の問は簡単化し過ぎたため、開ループ伝達関数と一巡伝達関数が両方\(G(s)\)で一致していました。一巡伝達関数で考えれば良い理由が書いていません。
ここでは、以下の2つのシステム(a),(b)を使用し、理由を探っていきます。
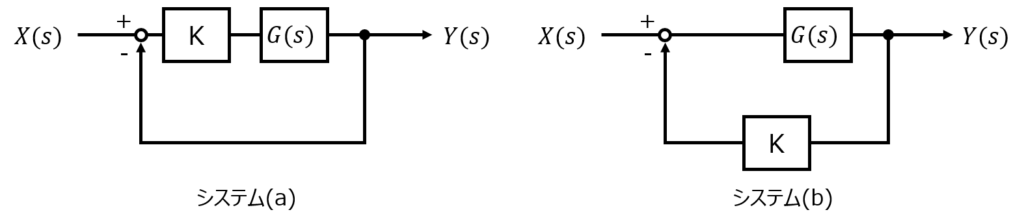
まず、システムaの閉ループ伝達関数ですが
\begin{eqnarray}G_{a}=\dfrac{G}{1+KG}\end{eqnarray}
システムbの閉ループ伝達関数は
\begin{eqnarray}G_{b}=\dfrac{KG}{1+KG}\end{eqnarray}
です。分子は違えど、分母(根)は一致していることが分かります。
前章の説明から、ナイキスト線図は、閉ループ伝達関数の根を座標変換して導いた結果ですので、安定性の評価に分子は関係ありません。
このように、フィードバックループに何か別の伝達関数が付いていたとしても根は変わらないので、一巡伝達関数を用いてシステムbもaと同じように考えても問題ありませんでした。
最後に
本問は大変難しいと思います。管理人も100%理解できている自信はありません。
ですが、昨今の教科書では証明が省かれているケースが多く、各々の安定判別方法を検討する際に適用する伝達関数を、「開」「閉」「一巡」どれなのか丸暗記になってしまっていると思います。
この時に困るのが、試験中にド忘れしてしまうことです。いつも解いている方法でどこか計算ミスしてしまうと、「あれ、考える伝達関数の対象間違えたっけ・・・?」と、どこか疑心暗鬼になるかもしれません。
そういった時、本記事で取り扱った、「各安定性判別方法の意味」を押さえておくことができれば、根拠を持ちながら自信を持って解答作成を進められると思います。
参考文献
自動制御理論:樋口 龍雄(著) 6章