【論理関数】n変数自己双対関数の個数、性質

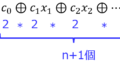
論理関数\(F=(x_{0},x_{1},x_{2},…,x_{n})\)に対して、\begin{eqnarray}F_{d}(x_{0},x_{1},x_{2},…,x_{n})=\overline{F( \overline{x_{0}},\overline{x_{1}},\overline{x}_{2},\ldots ,\overline{x_{n}})}\end{eqnarray}
で定義される関数を自己双対関数と言う。下記の問に答えよ。
(1)n変数自己双対関数は何個存在するか。
(2)2変数自己双対関数を論理式で全て挙げよ
(3)\(E=z･F(x,y)+\overline{z} ･F_{d}(x,y)\)は自己双対関数であることを示せ。
(4)\(F=x･y+x･G+y･H\)が自己双対関数であるとき、\(G\)と\(H\)の関係を示せ。

はじめに

論理関数の性質に関する問題は、東北大を初め、京大などで出題されます。閾値関数、対称関数、正関数など、様々な関数が存在しますが、本問ではまず自己双対関数の性質について例題を用いて説明していきます。

本問で覚えたいこと

ある3変数自己双対関数\(F\)の真理値表を作成してみましょう。\((x,y,z)=(0,0,0),(0,0,1),(0,1,0)\)のように、\(z\)に1ずつ加算していった場合を考えます。

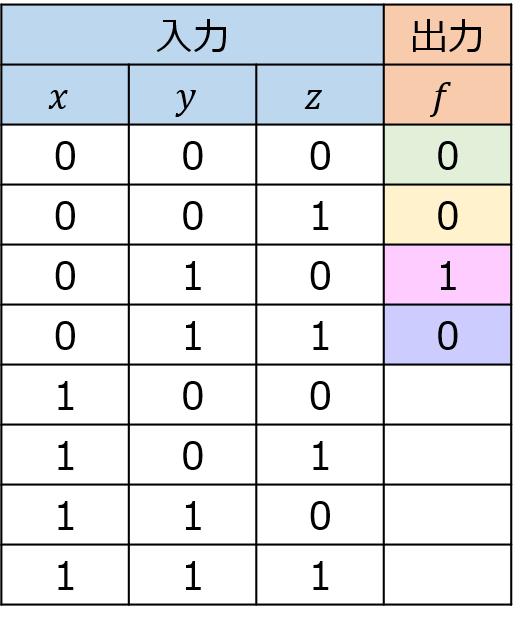
上記のような真理値表だったとします。実は、残りの下半分は一意に決まります。

自己双対関数の性質により、変数のbitを反転させた入力をすると、反転前の入力に対する出力値のnotを取った値を出力します。

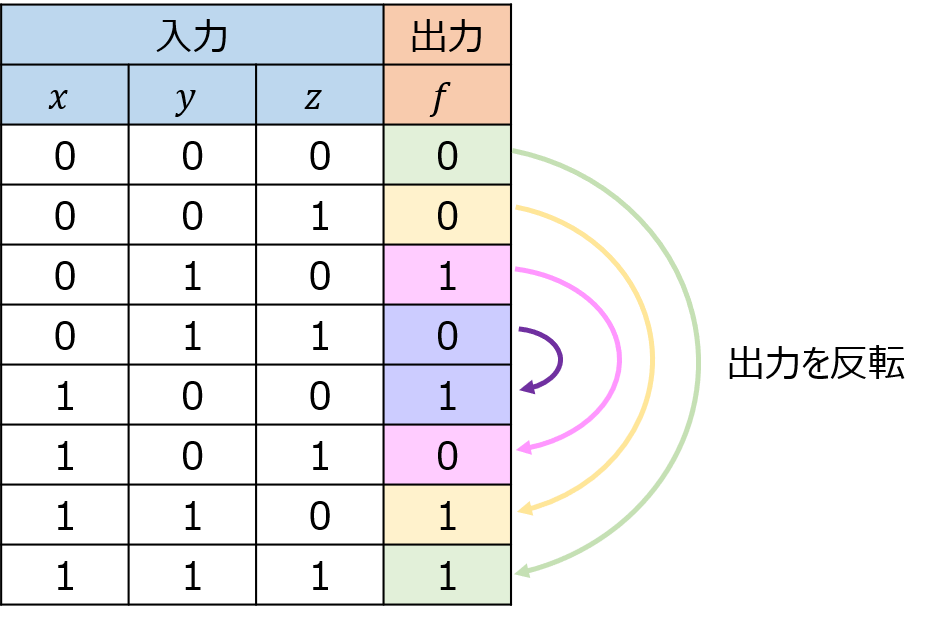
上図は、(0,1,1)で1を出力するのですから、(1,0,0)ならば0を出力することになります。

これを他の組み合わせに対しても考えることで、下半分は一意に決まります。

２．については(3)で用います。\(F(x,y)\)と\(F_{d}(x,y)\)を組み合わせた関数は、ドモルガン律で分解することにより、\(F(x,y)\)は\(F_{d}(x,y)\)に、もう一方も逆になることで、等価になりやすいです。

解答例

(1)n変数自己双対関数の個数

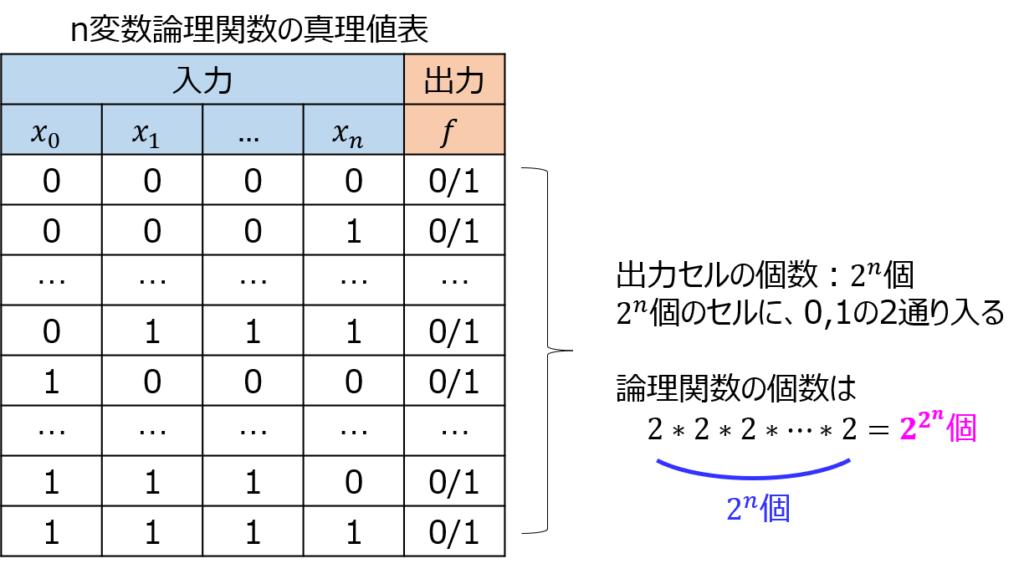
まず、n変数論理関数の個数を考える。真理値表より、入力の組み合わせは\(2^{n}\)個存在し、それぞれの入力に対する出力は0,1の2通りあるため、\(2*2*2*…*2\) を \(2^{n}\)回乗算するので、\(2^{2^{n}}\)個存在する。

一方、n変数双対関数の個数を考える。前章の説明から、入力の組み合わせ半分に対する出力が決まれば、もう半分は一意に決まる。よって、入力の組み合わせは\(2^{n-1}\)個存在する。出力は0,1の2通り変わらず存在するため、\(2^{2^{n-1}}\)個存在する。

(2)2変数双対関数の論理式ついて

前章の説明から、真理値表の上半分を決めて、下半分の出力を反転させれば良い。

この考えから、2変数双対関数の取りうる真理値表は\(2^{2^{2-1}}=4\)通り存在する。

実際の真理値表は、下記になる。

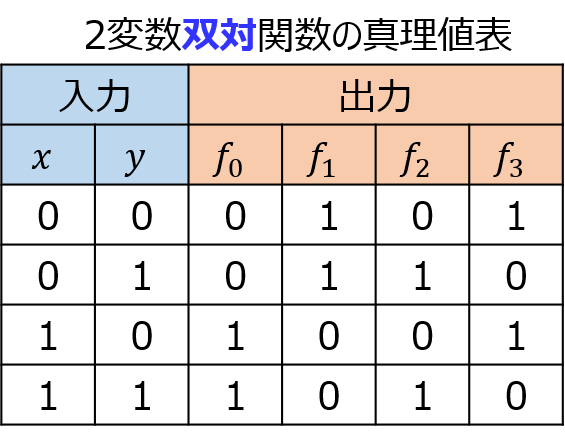
左から順に、\(f_{0}=x,f_{1}=\overline{x},f_{2}=y,f_{3}=\overline{y}\)になる。

(3)自己双対関数の証明問題

与えられた論理関数\begin{eqnarray}E=z･F(x,y)+\overline{z} ･F_{d}(x,y)\end{eqnarray}に対し

\begin{eqnarray}E_{d}=\overline{\overline{z}･F(\overline{x},\overline{y})+z ･F_{d}(\overline{x},\overline{y})}\end{eqnarray}を考え、論理関数\(E\)と等価であることを示す。

ドモルガン律を用いて、(3)式を変形すると

\begin{align}(3)&=\overline{\overline{z}\cdot F\left( \overline{x},\overline{y}\right) }\cdot \overline{z \cdot F\left( \overline{x},\overline{y }\right) } \\ &= \left( z+F_{d}\right) \cdot \left( z+F\right) \\ &= z･F(x,y)+\overline{z} ･F_{d}(x,y) +F(x,y)F_{d}(x,y) \\ &= E+F(x,y)F_{d}(x,y)\end{align}

(i) \(F(x,y)F_{d}(x,y)=1\) すなわち \((F,F_{d})=(1,1)\)のとき

(2)式は、\(E=z+\overline{z}=1\) よって、\(E=E_{d}\)であることが確認できた。

(ii)\(F(x,y)F_{d}(x,y)=0\) すなわち \((F,F_{d})=(0,0),(1,0),(0,1)\)のとき

(6)式より、\(E=E_{d}\)である。

よって、全ての\(F,F_{d}\)の組み合わせに対し、\(E=E_{d}\)であるので、\(E\)は自己双対関数である。

(4)GとHの関係

(3)より、\(E_{d}=z･F(x,y)+\overline{z} ･F_{d}(x,y) +F(x,y)F_{d}(x,y)\) は自己双対関数。

\(F=x･y+x･G+y･H\)に対し、\(x→F(x,y),y→F_{d}(x,y)\)と置き換えると、\(z→G\)と置き換えられる。

\(\overline{z}=H\)なので、求める\(G\)と\(H\)の関係は、\(H=\overline{G}\)

最後に

本記事では、自己双対関数について紹介しました。一方で、逆の性質を持つ関数もあります。

\begin{eqnarray}F_{d}(x_{0},x_{1},x_{2},…,x_{n})=F( \overline{x_{0}}.,\overline{x_{1}},\overline{x}_{2},\ldots \overline{x_{n}})\end{eqnarray}

と、右辺の\(f\)に対しnotを付けない場合は、自己反双対関数と呼びます。この個数も、2章と同様の考え方で\(2^{2^{n-1}}\)個になります。

問題で問われている関数は、どちらの関数に対してか、確認してから解答に移ると良いと思います。

参考文献

解法と演習 大学院入試問題<情報通信系>：関 正治(著),陳 啓浩(著),姫野 俊一(著) P32