比較器とは
ある2つの数値A,Bを比較し、どちらが大きいか判定する演算器です。
判定方法はシンプルです。人間の目で10進数の数値を大小比較するときに考えることを2進数に落とし込むだけです。
もし、A=33,B=4ならば、どちらが大きいかは明白です。A=33です。
どのように判断されましたでしょうか?Bは1桁で、Aは2桁と、そもそもAの方が桁数が多いと答える方が多そうです。
この考え方を論理回路でも用います。
A=33を2進数にすると、[100001]です。B=4を2進数にすると、[100]です。
2進数も、桁数の多いAが大きいことが一目で分かりました。
もし同じ桁数の場合は、1桁目から数字を比較していきます。この動作内容を次章で示します。
比較器の演算内容
Nbitの数値 \(A=[a_{N}a_{N-1} \ldots a_{1}],B=[b_{N}b_{N-1} \ldots b_{1}]\)の比較を考えます。
前章で示した指針通り、\(a_{1},b_{1}\)の比較をまず行います。変数(i=1,2,\ldots,N\)を用いて一般化し、\とし、A,Bを構成するビットのうち、\(i\)ビット目の比較結果を下記のフラグで表します。
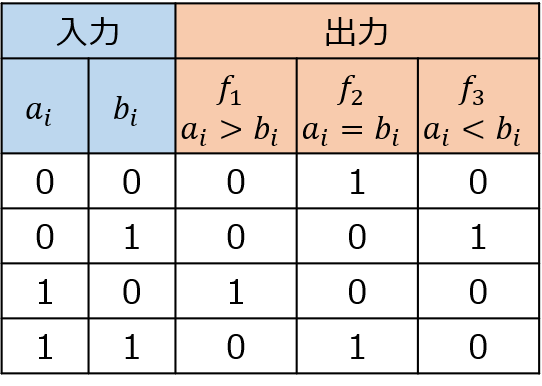
- \(a_{i}>b_{i}\)のとき、\(f_{1}=1\)、\(f_{1}=a_{i}\overline{b_{i}}\)
- \(a_{i}=b_{i}\)のとき、\(f_{2}=1\)、\(f_{2}=\overline{f_{1}}・\overline{f_{3}}\)
- \(a_{i}<b_{i}\)のとき、\(f_{3}=1\)、\(f_{3}=a_{i}\overline{b_{i}}\)
\(i\)ビット目までのAとBの大小関係の比較結果を、A>B、A=B、A<Bの順に\(f_{1,i},f_{2,i},f_{3,i}\)とします。
それぞれの成立条件は、下記のように考えることができます。
- \(f_{1,i}=1\):
i bit目のAとBの数値がAの方が大きい または
i bit目の数値はAとB等しいが、i-1bit目までのAとBの数値がAの方が大きい
\(f_{1,i}=f_{1}+f_{2}・f_{1,i-1}\) - \(f_{2,i}=1\):
i bit目のAとBの数値が等しい かつ i-1 bit目までのAとBの数値も等しい
\(f_{2,i}=f_{2}+f_{2}・f_{2,i-1}\) - \(f_{3,i}=1\):
i bit目のAとBの数値がBの方が大きい または
i bit目の数値はAとB等しいが、i-1bit目までのAとBの数値がBの方が大きい
\(f_{3,i}=f_{3}+f_{2}・f_{3,i-1}\)
上記が全てです。これが分かれば後は論理式の通り回路を組むだけです。
比較器の回路設計
\begin{aligned}f_{0}&=a_{i}\overline{b_{i}}=a_{i}\left( \overline{a_{i}}+\overline{b_{i}}\right)=a_{i}\overline{a_{i}b_{i}} \\ f_{2}&=f_{2}=\overline{f_{1}}・\overline{f_{3}}=\overline{f_{1}+f_{3}} \\ f_{3}&=\overline{a_{i}}b_{i}= b_{i}\left( \overline{a_{i}}+\overline{b_{i}}\right)=b_{i}\overline{a_{i}b_{i}}\end{aligned}
を利用して、下記の比較器を設計できます。
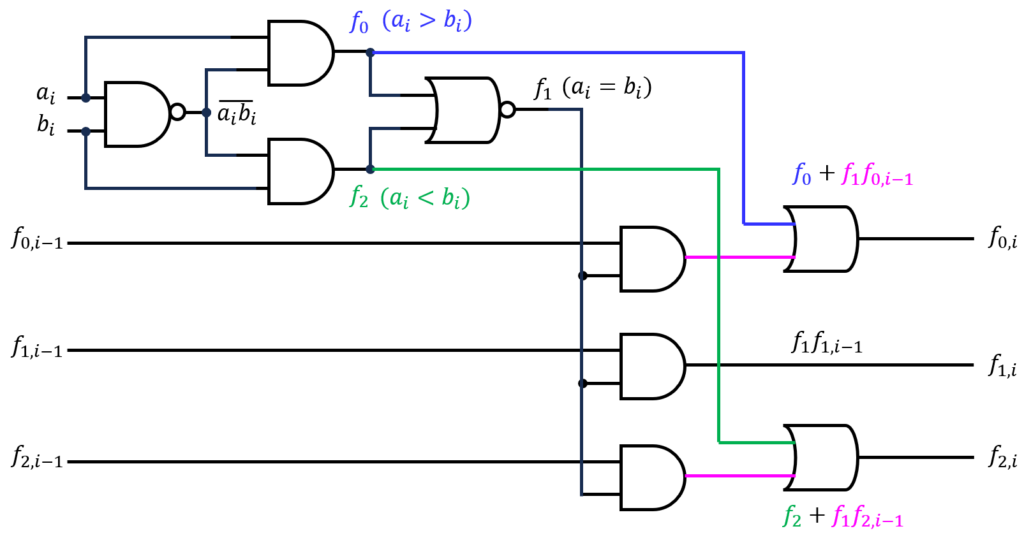
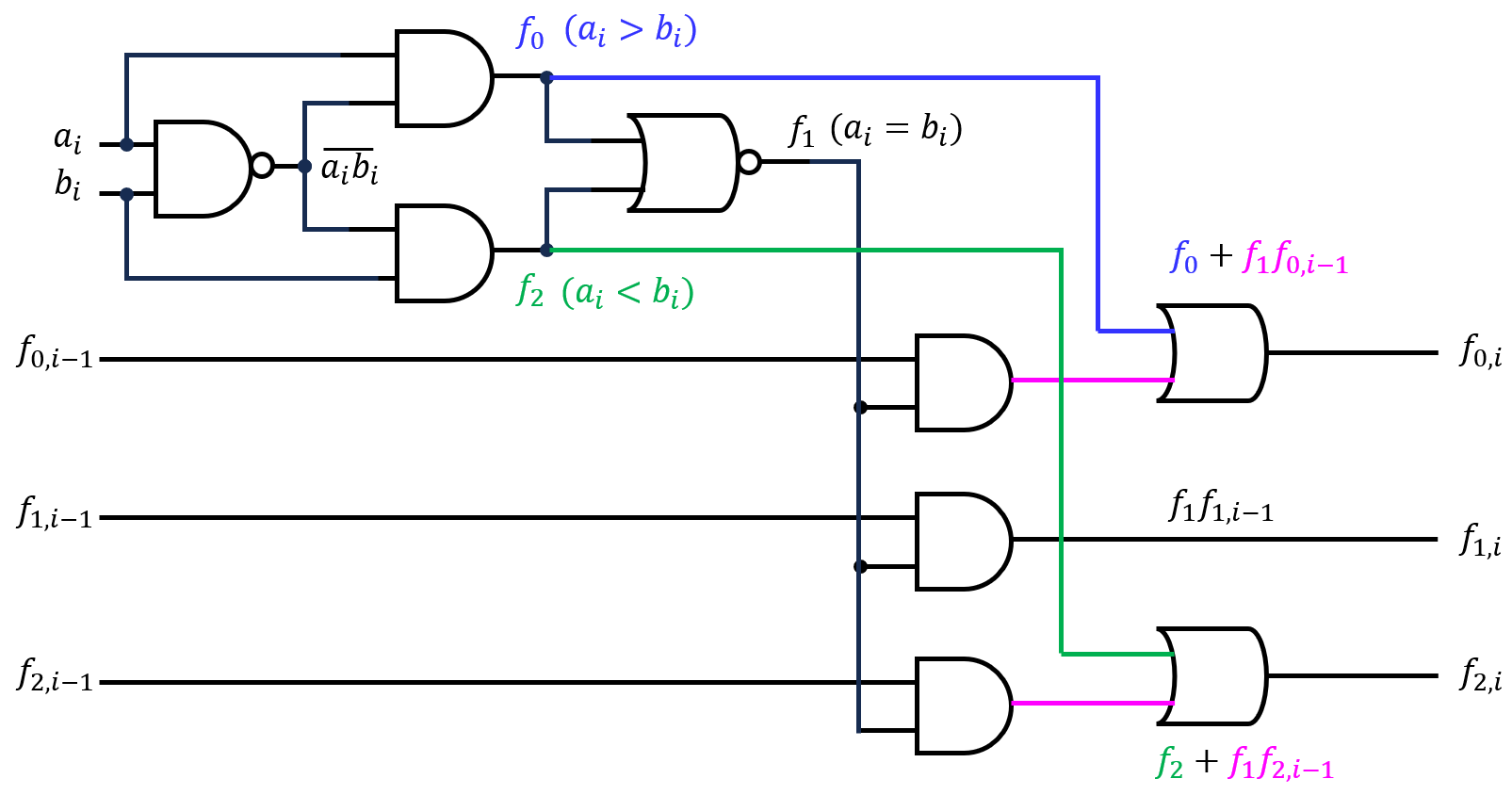
一般化しているため\(i\)での記載ですが、実際は\(i=1~N\)まで上記の回路を繋げていくことで設計できます。
なお、比較する数値の桁が一致しない場合は、桁が足りない側のbitに0を入れます。
例)A=33の2進数[100001]に対し、B=4を[000100]とします。
大きい方の数値を出力する論理回路設計
前節までは、二つの数値A,Bを比較した結果を3つのフラグで表しました。
問題によっては、フラグだけでなく大きい方の数値を出力すること。なる追加条件があります。
本節では、この実現方法を考えていきます。
まず、前節で算出したフラグが役立ちそうです。\(f_{1}=1\)ならばAを、\(f_{3}=1\)ならばBを出力すれば良いです。
これをAND、ORで実現すると、以下のような回路で表すことができます。
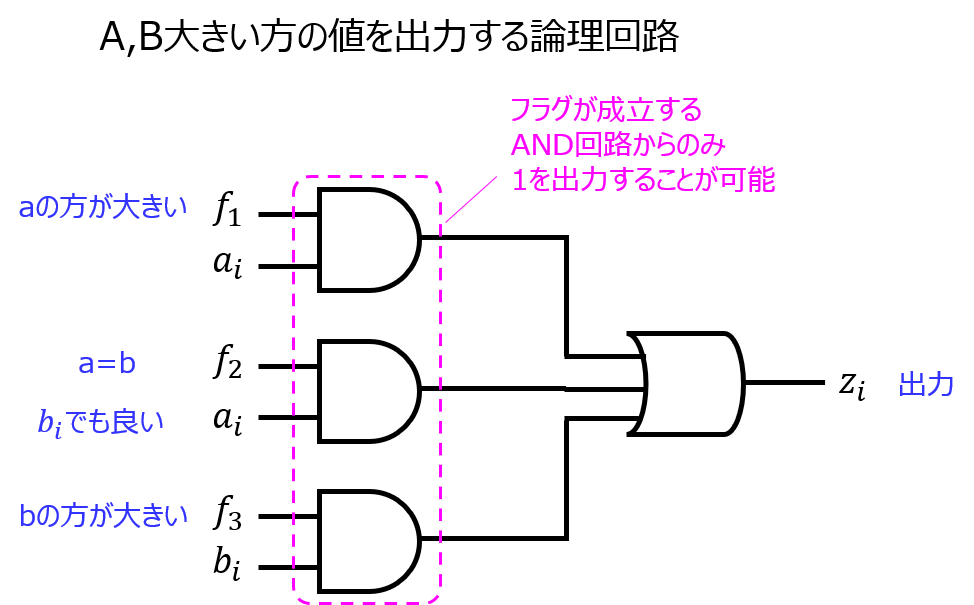
ちょっとトリッキーですが、以下の考え方で設計しました。
\(f_{1}=1\)のときは\(a_{i}\)のbitを出力、\(f_{3}=1|)のときは\(b_{i}\)のbitを出力すればよい。
AND回路を採用すれば、フラグ0が成立している側の数値に関しては出力に影響しないです。フラグ=1が成立している側の数値の対応するbitが1の場合、ANDが成立するため、この先のORで出力する。
これを\(i=1\)から\(N\)に関して繰り返し行っていけば良いです。
最後に
大きい方の数値を出力する回路設計は、教科書では見たことなく、本サイトオリジナルの設計です。2進数ならば問題無い認識ですが、誤りがある場合はご教授お願いいたします。
他、もっと良い設計方法があればご教授下さると幸いです。
参考文献
ディジタル情報回路 (第2版):清水 賢資 (著) P116,117