ラウス・フルビッツの安定判別法の例題

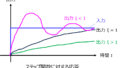
開ループ伝達関数\(G\left( s\right) =\dfrac{1}{2s^{4}+s^{3}+3s^{2}+5s+9}\)が安定であるか、以下の安定判別法それぞれを用いて示せ。
(1)ラウスの安定判別法
(2)フルビッツの安定判別法
自動制御理論　樋口龍雄(著) P127より(1)を引用。(2)は創作

はじめに
ラウス・フルビッツの安定判別法の説明
解答例
最後に
参考文献

はじめに

以前の記事にて、伝達関数の極が負の領域にあれば、システムが安定であることを説明しました。入力を逆ラプラス変換すると、exp(t)項のかっこ内が負になるため、\(t→∞\)の極限を考えると収束するからです。

ですので、閉ループ系の極を表現する特性方程式\(1+G(s)\)の極を導き、逆ラプラス変換できれば伝達関数から直接安定性を判別できます。

ただ、この方法は手計算では限界が来ます。特に本問のようにsの項が4次以上の場合は、より厳しいです。4次方程式を因数分解して解くことは人間の手では難しいためです。

このような時に出てくるのが、ラウス・フルビッツの安定判別法です。2通りの方法で判別できます。

数学的に厳密に説明することは工学部のカリキュラムでは難しいです。本記事では、決まり事を紹介し、それに準じて安定判別していきます。

ラウス・フルビッツの安定判別法の説明

ラウスの安定判別法とは

特性方程式 \(1+G(s)\)が、

\begin{eqnarray}a_{0} s^{n}+a_{1} s^{n-1}+a_{2} s^{n-2}+ \cdots + a_{n-1} s^{1}+a_{0}=0\end{eqnarray}で表されるとき、下記の配列を計算します。

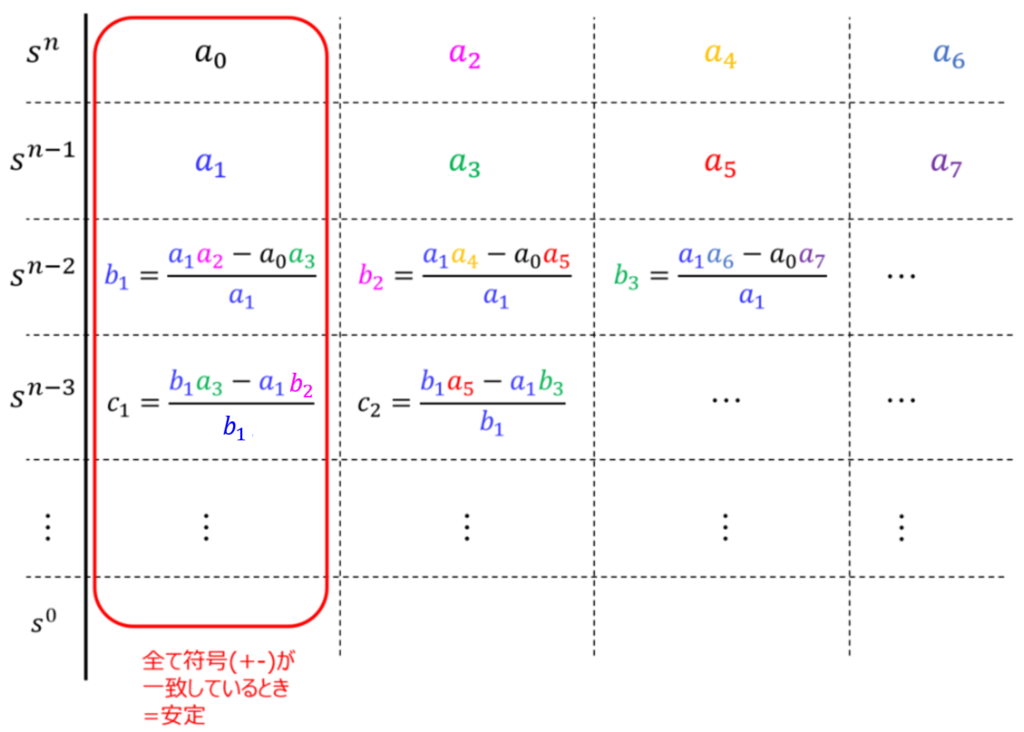
計算が少々面倒ですが、\(s^{n-2}\)以降の計算において、分母と分子の計算で使用する値は一番左の列の値であることを覚えておけば何とかなりそうです。

一番左の列が全て同じ符号ならば安定になります。一行目から見ていき、正→負または負→正に置き換わる回数分、不安定極が存在します。

フルビッツの安定判別法とは

ラウスの安定判別法より簡易的な計算で安定性を判断できます。

行列式を地道に計算するだけで良いので、個人的には、こちらの方法をオススメします。

同じく、特性方程式((1)式)について、以下の条件が成立するとき安定です。

フルビッツの安定判別法を使用した時の安定判別条件

係数\(a_{0},a_{1},a_{2},\cdots,a_{n-1},a_{n}\)が全て正 (0はNG)
以下の行列式が全て正であること

\begin{vmatrix} a_{1}a_{3} \\ a_{0}a_{2} \end{vmatrix}

\begin{vmatrix} a_{1} & a_{3} & a_{5} \\ a_{0} & a_{2} & a_{4} \\ 0 & a_{1} & a_{s} \end{vmatrix}

・・・

\begin{vmatrix} a_{1} & a_{3} & a_{5} & \ldots & a_{2n-3} \\ a_{0} & a_{2} & a_{4} & \ldots & a_{2n-4} \\ 0 & a_{1} & a_{3} & \ldots & a_{2n-5} \\ 0 & a_{0} & a_{2} & \ldots & a_{2n-6} \\ 0 & 0 & a_{1} & \ldots & a_{2n-7} \\ \vdots & \vdots \\ 0 & 0 & 0 & \ldots & a_{n-1} \end{vmatrix}

要は、特性方程式の係数とそれにかかわる行列式が全て正ならば良いです。

これならば、行列式を機械的に計算していくだけなので、幾分か楽になります。

ただ、ラウスの安定判別法とは違い、不安定極の数を調べることはできないです。ここは注意が必要です。

行列式は、上から係数を埋めていくのではなく、下から埋めていくことに注意しましょう。