はじめに
本記事は、前回の記事の続きです。
詳解電磁気学演習は、多数の問題が収録されており、電磁気学の勉強をする上で必ず持っておきたい本です。
一方で、「全部解くことはできないため、試験で出てきそうな問題を解きましょう。」と本サイト、他者様問わず、よく説明しています。
院試勉強を始めた段階だと、具体的にどのような問題が頻出なのか判断付かないと思います。
そこで、本サイトでは、是非とも解いておきたい重要問題を章ごとに紹介しています。
詳解電磁気学演習の章立て
- 真空中の静電界
- 真空中の電荷分布による静電界
- 電気力線とガウスの定理
- 真空中の導体系
- 真空中の導体系一般論
- 静電容量とその配列
- 誘電体中の静電界
- 誘電体中の静電界
- 誘電体でのエネルギーと力
- 特殊な誘電体
- 静電界の特殊解法
- 電気映像
- Laplace方程式の解
- 等角写像
- 定常電流
- Ohmの法則
- 回路網の電流
- 連続導体内の電流
- 電力・Joule熱
- 熱電現象
- 静磁界
- 真空静磁界
- 磁性体
- 電気磁気の相互作用Ⅰ:定常電流による磁界
- 定常電流による磁界
- 磁気回路
- 磁界が電流におよぼす力
- 電気磁気の相互作用Ⅱ:電磁誘導
- 電磁誘導
- インダクタンスの算出
- インダクタンスと電磁現象
- 非定常電流の諸現象
- 過渡現象
- 交流
- 交流理論
- 交流回路網
- 電磁波
- 電磁波の伝搬
- 電磁波の立体回路
- 電磁波の放射
- 電気力学以降は、工学部電気系の院試で出題されているところはあまり見たことがありません。省略します。
問題のレベル分け
「院試に出てくる問題」及び「院試問題を解くために必要な知識を習得する問題」という観点で紹介しますが、どうしても問題のレベルは存在します。
そこそこ勉強している方に基礎問題の紹介しても仕方ないと考えますので、3段階で分けることにします。
☆★★:基礎(高校レベル)
☆☆★:標準(大学講義レベル)
☆☆☆:応用(院試レベル)
オススメ問題
8章:電気磁気の相互作用Ⅱ:電磁誘導
本章は、重要な問題が多数あります。
それ故、記事が長くなります。
ご自身が受けようとしている大学にフォーカスして読んでいく方が良いかもしれません。
電磁誘導
大学受験で頻出分野です。院試でも変わらず問われます。
問題[1] 電磁誘導の積分系から微分形への導出 ☆☆★
対策になりそうな大学:東北大
本問は、解き方を暗記した方が良いです。ストークスの定理を使用することを知っていなければ、解くことはできません。
問題[2] 回路が磁界中で移動変形するときの起電力 ☆☆★
対策になりそうな大学:阪大、名大
大学受験では、このタイプの起電力問題が良く出題されます。
上記の大学では、院試でも変わらず出題されます。
問題[4] 一様磁界の中でコイルを回転させるときの誘導起電力 ☆★★
対策になりそうな大学:全般
大学受験の知識で解けます。頭の中で即答できるならば、書いて確かめる必要はありません。
問題[9-1] レールの上を導体が動くときの誘導起電力 ☆★★
対策になりそうな大学:全般
大学受験の超頻出問題です。懐かしみ半分で解いてみてはいかがでしょうか。
高校生の時は流れ作業で解いていましたが、実は問題2の応用版であることが分かります。
問題[10] 一様な磁場内で導体が回転するときの誘導起電力 ☆★★
対策になりそうな大学:全般
同じく大学受験の超頻出問題です。鎖交面積\(dS\)が、レールの上を動くときと回転するときで変わることだけ気を付けましょう。
インダクタンスの算出
前節に引き続き、頻出分野になります。
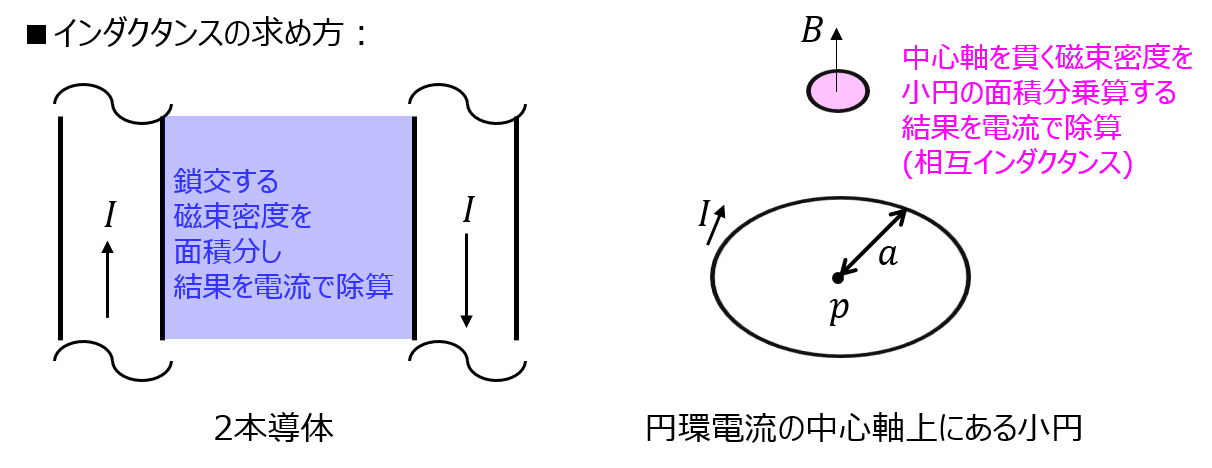
院試では、\(\phi=BS=LI\)の関係からインダクタンスを求めることが多いです。
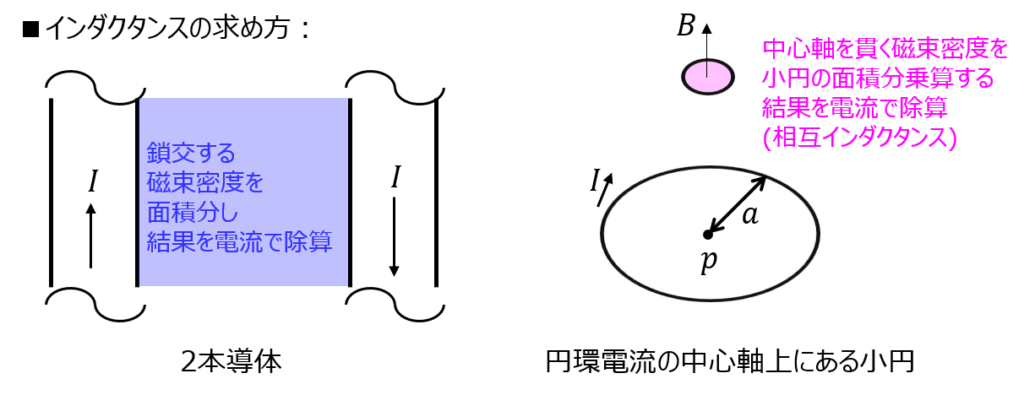
問題[17] 2本の無限長導線の自己インダクタンス ☆☆★
対策になりそうな大学:全般
まず、アンペールの法則を重ね合わせ、無限長導線間の磁束密度分布を求めます。その後、磁束密度を面積分することで鎖交磁束を求めます。
これを電流Iで割ることで自己インダクタンスが求まります。
大学の電磁気学で、自己インダクタンスを求める際の定石解法になります。是非マスターしましょう。
問題[18] 2つの長方形コイルの相互インダクタンス ☆☆★
対策になりそうな大学:名大
同じ問題が2022年に出題されました。
鎖交磁束を手計算で求めるのは困難ですので、ノイマンの式を用います。
線積分で相互インダクタンスを求められることから、何とか手計算で求められる範囲に落ち着きます。
問題[19-3] 大地と正対する導体の自己インダクタンス ☆☆★
対策になりそうな大学:東北大
鏡像法の知識を用います。鏡像導体から発生する磁場と重ね合わせた磁束密度の算出ができれば、あとは問題17と同じ方法で解けます。
問題[23] 円形コイルと小円形コイルの相互インダクタンス ☆☆★
対策になりそうな大学:全般
院試頻出です。
同じ大きさのコイルが正対しても、コイルを貫く磁束密度分布が場所によって異なることから、手計算で求めるには中々厳しいです。
ですが、本問の場合、小円形コイルを貫く磁束密度は一定とみなすことができます。よって、手計算で解きやすい形になりますので、院試で好んで出題されます。
問題[27-1] 空隙のある環状ソレノイドコイルの自己インダクタンス ☆☆★
対策になりそうな大学:全般
磁気回路法を用います。
まず、回路方程式により\(\phi\)を求めます。その後、\(\phi=LI\)を利用することで、自己インダクタンスが求まります。
結局、\(\phi\)を求める手段が、磁束密度の積分か、磁気回路であるかの違いです。
問題[27-1] 同軸ケーブルの自己インダクタンス ☆☆☆
対策になりそうな大学:全般 (特に東北大と大阪公立大)
積分して磁束密度を求める基本方針は同じですが、電流が一様に流れていることがポイントです。
鎖交巻き数が\(N=\dfrac{c^{2}-r^{2}}{c^{2}-b^{2}\)と、半径\(r\)により変化します。
これにより、鎖交磁束\(\Phi\)の積分計算が複雑になります。難しい問題です。
インダクタンスと電磁現象
問題[38] 磁界が電流におよぼす力とエネルギーの関係 ☆☆★
対策になりそうな大学:全般
力を積分するとエネルギーであることを、電磁気学の分野においても証明します。
意外と院試で出てきます。同じ問題が出てこないにしても、本問で問われる事実を別の問題で使うことが良くあります。
問題[39] 磁気エネルギーを用いた自己インダクタンスの算出 ☆☆★
対策になりそうな大学:全般
前節の方法でも自己インダクタンスは求まりますが、\(U=\dfrac{1}LI^{2}\)でも求めることが出来ます。
前節は面積分、本問は体積分を用いて\(L\)を求める。と覚えましょう。
非定常電流の諸現象
本節から、試験範囲に含まれない大学が出てきます。(電磁波の知識も出てくるため)
試験範囲としてグレーですが、万全を期すために演習することをオススメします。
問題[45] 変位電流の算出 ☆☆★
対策になりそうな大学:全般
\(\dfrac{dD}{dt}\)を使用すれば簡単に解けます。
解き方が瞬時に思い浮かぶなら、スルーでも問題無いです。電場ではなく、電束密度を微分することだけ注意しましょう。
問題[47] 伝導電流と変位電流の比 ☆☆★
対策になりそうな大学:全般
今までの知識の確認です。それぞれの電流の定義式さえ頭に入っていれば、難なく解答できると思います。
問題[49] 表皮効果の導出 ☆☆☆
対策になりそうな大学:全般
本節におけるもっとも重要な問題です。阪大、東北大で同じ問題が出たことがあります。
微分方程式に対し、解を仮定して解くことから、初見で解くことは難しいです。
何度も繰り返し、何も見ずに解けるようにしましょう。
過渡現象
電気回路に関する章であることから、電磁気学の院試では出てこないです。省略します。
9章 交流
8章:過渡現象と同じです。電気回路の分野なので、特にオススメする問題はありません。
最後に
次回、10章:電磁波問題を解くうえでのオススメ記事を紹介していきます。
ここまでくると出題される大学が限られてきます。是非、自身が受験する大学院の試験範囲をチェックし、10章含めて対策するか、事前検討することをオススメします。