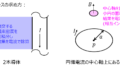- はじめに
- 詳解電磁気学演習の章立て
- 問題のレベル分け
- オススメ問題
- 6章:静磁界
- 7章:電気磁気の相互作用Ⅰ
- 定常電流と磁界
- 問題[4] 直線導体から発生する磁場 ☆☆★
- 問題[6] 無限円柱から発生する磁場 ☆☆★
- 問題[8] 2本の無限長導体から発生する磁場の重ね合わせ ☆☆★
- 問題[11] 円環電流から発生する磁場 ☆☆★
- 問題[11-4] 半円と直線導体から発生する磁場 ☆☆★
- 問題[15] ソレノイドコイルから発生する磁場 ☆☆☆
- 問題[19] 帯電した導体球を回転した際の磁場 ☆☆☆
- 問題[22] 無限長の薄板に流れる電流から発生する磁場 ☆☆☆
- 問題[24] 無限長導体の一部に穴が開いた場合の発生する磁場 ☆☆★
- 問題[24-2] 同軸ケーブルから発生する磁場 ☆☆★
- 問題[25] 円環電流のベクトルポテンシャル ☆☆☆
- 問題[25-1] 有限長直線導体のベクトルポテンシャル ☆☆☆
- 磁気回路
- 磁界が電流におよぼす力
- 定常電流と磁界
- 最後に
はじめに
本記事は、前回の記事の続きです。
詳解電磁気学演習は、多数の問題が収録されており、電磁気学の勉強をする上で必ず持っておきたい本です。
一方で、「全部解くことはできないため、試験で出てきそうな問題を解きましょう。」と本サイト、他者様問わず、よく説明しています。
院試勉強を始めた段階だと、具体的にどのような問題が頻出なのか判断付かないと思います。
そこで、本サイトでは、是非とも解いておきたい問題を章ごとに紹介しています。
詳解電磁気学演習の章立て
- 真空中の静電界
- 真空中の電荷分布による静電界
- 電気力線とガウスの定理
- 真空中の導体系
- 真空中の導体系一般論
- 静電容量とその配列
- 誘電体中の静電界
- 誘電体中の静電界
- 誘電体でのエネルギーと力
- 特殊な誘電体
- 静電界の特殊解法
- 電気映像
- Laplace方程式の解
- 等角写像
- 定常電流
- Ohmの法則
- 回路網の電流
- 連続導体内の電流
- 電力・Joule熱
- 熱電現象
- 静磁界
- 真空静磁界
- 磁性体
- 電気磁気の相互作用Ⅰ:定常電流による磁界
- 定常電流による磁界
- 磁気回路
- 磁界が電流におよぼす力
- 電気磁気の相互作用Ⅱ:電磁誘導
- 電磁誘導
- インダクタンスの算出
- インダクタンスと電磁現象
- 非定常電流の諸現象
- 過渡現象
- 交流
- 交流理論
- 交流回路網
- 電磁波
- 電磁波の伝搬
- 電磁波の立体回路
- 電磁波の放射
- 電気力学以降は、工学部電気系の院試で出題されているところはあまり見たことがありません。省略します。
問題のレベル分け
「院試に出てくる問題」及び「院試問題を解くために必要な知識を習得する問題」という観点で紹介しますが、どうしても問題のレベルは存在します。
そこそこ勉強している方に基礎問題の紹介しても仕方ないと考えますので、3段階で分けることにします。
☆★★:基礎(高校レベル)
☆☆★:標準(大学講義レベル)
☆☆☆:応用(院試レベル)
オススメ問題
6章:静磁界
真空静電界
1,2章(クーロンの法則、真空静電界)の磁気バージョンです。
磁石が引き合う、反発し合うのと同様に、磁荷によるクーロンの法則を中心に本節で扱います。
しかし、院試ではあまり出題されません。
特定の大学志願者だけ、目を通すと良いでしょう。
問題[1] 小磁石A,Bの距離 ☆☆★
対策になりそうな大学:大阪公立大
クーロンの法則の公式において、電荷\(q\)を磁化\(M\)に置き換えるだけです。
後は、高校の計算問題で解を求められます。
問題[4] 磁気モーメントが異なる磁石を同一平面上に置いた時の関係 ☆☆★
対策になりそうな大学:大阪公立大
本節において、この問題が最も重要です。全く同じ問題が上記大学で出題されたことがありました。
加えて、磁石の問題を解くうえで定石となる考え方が多数詰まっています。
他大学志望者と言えども、本問だけは練習した方が良いでしょう。
補足
本節で取り上げる問題は上記2問です。他の問題は、計算自体が複雑なため、院試ではあまり出題されないと思います。
磁性体
本節は目を通した方が良いです。
オススメする問題は少ないですが、磁力線の動きを理解していないと解けない問題が多いです。
モータなどの電気機器、ハードディスクなどの磁気デバイスの動作を理解する上で本章の勉強は必ず役立ちます。
また、相変わらず境界条件が出題されます。
問題[15] マクスウェルの応力(磁気バージョン) ☆☆★
対策になりそうな大学:全般
誘電体と同じく磁性体でも同じ問題が出ます。\(ε\)を\(\mu\)に、\(E\)を\(H\)に置き換えると同じ結果になります。
問題[16] 異なる磁性体の境界条件 ☆☆★
対策になりそうな大学:全般
この問題は必ずやった方が良いです。普段暗記して使っている境界条件を証明できます。
神戸大を初め、問題として出題されることもあります。
問題[20-3] 地球の緯度と伏角の関係 ☆☆☆
対策になりそうな大学:京大(通信情報)
全く同じ問題が上記大学で出題されたことがあります。初見で解くことは厳しいので、必ず演習しましょう。
問題[24] 異なる磁性体に入射した磁場の境界条件 ☆☆★
対策になりそうな大学:全般
誘電体に変わっただけの全く同じ問題を以前の記事で紹介しました。磁場になっても変わらず境界条件に関する基本的な考え方を学べます。是非演習したい問題です。
問題[24-1] 異なる磁性体に入射した磁場の境界条件(垂直/平行な場合) ☆☆★
対策になりそうな大学:全般
問題24と殆ど同じです。境界面の平行成分に対し、磁場\(H\)が連続。垂直成分の場合、磁場\(B\)が連続なので、この関係を使えば一発で解けます。
7章:電気磁気の相互作用Ⅰ
8章と並んで院試頻出です。
定常電流と磁界
ビオサバールの法則、アンペールの法則を使い分けて問題を解いていきます。基本的な考え方はこちらの記事で紹介しています。
復習しながら読んでいくと、より理解が深まると思います。
問題[4] 直線導体から発生する磁場 ☆☆★
対策になりそうな大学:全般
電磁気学の教科書で、必ずと言って良いほど出てくる問題です。本によって解き方は異なりますが、詳解電磁気学演習で紹介している方法が最もオーソドックスで覚えやすいと思います。
問題[6] 無限円柱から発生する磁場 ☆☆★
対策になりそうな大学:全般
アンペールの法則を用いて磁場を算出する基本的な問題です。ただの流れ作業ではなく、無限長だから適用できる。ということを本問を通して確認すると良いです。
問題[8] 2本の無限長導体から発生する磁場の重ね合わせ ☆☆★
対策になりそうな大学:全般
クーロンの法則でも似たような問題を紹介しました。ベクトル分解し、基準の方向とその垂直方向に分けることが出来れば、難なく解けます。
問題[11] 円環電流から発生する磁場 ☆☆★
対策になりそうな大学:全般
先述と同じく、電磁気学の教科書で必ずと言って良いほど紹介される問題です。無限長では無いため、ビオサバールの法則を用いて解きましょう。
その際は、半径方向の磁場は打ち消し合うことをお忘れなく。垂直方向だけ足し合わせましょう。
問題[11-4] 半円と直線導体から発生する磁場 ☆☆★
対策になりそうな大学:北大
電流の流れる方向と目標点までのベクトルが一致しているとき、磁場0になります。(外積=0になるため。)
ですので、結局は半円部分の磁場しか考えなくて良くなります。
問題[15] ソレノイドコイルから発生する磁場 ☆☆☆
対策になりそうな大学:阪大
問題11の発展版です。巻き数分、角度も込みで積分していきます。
同様の問題が阪大から出題されたことがあります。同大学ではソレノイドコイルが頻出です。少し難しいですが、是非自分のものにしましょう。
問題[19] 帯電した導体球を回転した際の磁場 ☆☆☆
対策になりそうな大学:北大
同様の問題をこちらの記事で紹介したことがあります。電流=面電荷*速度(周波数)と考えることができます。
あとは、微小円環電流に区間分割し、積分して求めるのみです。
問題[22] 無限長の薄板に流れる電流から発生する磁場 ☆☆☆
対策になりそうな大学:神戸大
問題4の発展版です。ビオサバールの法則を用いて、直線から発生する磁場を求めたのち、これを無限長の区間に対して積分していきます。
計算が複雑ですが、演習しがいのある問題です。
問題[24] 無限長導体の一部に穴が開いた場合の発生する磁場 ☆☆★
対策になりそうな大学:全般
有名問題です。まず、穴が開いてない場合の発生する磁場をアンペールの法則を用いて求めます。その後、穴が開いている部分を逆向きの電流が流れているとし、その分の磁場を求めます。
結果を足し合わせ、答えが求まります。
問題[24-2] 同軸ケーブルから発生する磁場 ☆☆★
対策になりそうな大学:全般
これも有名問題です。同軸ケーブルの中空部分で磁場が発生します。
しかし、外側円筒内に入ってからは、減衰していきます。
問題[25] 円環電流のベクトルポテンシャル ☆☆☆
対策になりそうな大学:阪大、名大
ベクトルポテンシャルを好んで出す大学を受験する際は必ず演習しましょう。
(2)の近似計算まではやらなくて良いですが、(1)のベクトルポテンシャルを極座標成分表記する部分は何度も練習しましょう。
問題[25-1] 有限長直線導体のベクトルポテンシャル ☆☆☆
対策になりそうな大学:阪大、名大
問題25と同様の理由です。ベクトルポテンシャルを問われるとしたら、こちらの形式の場合もあります。
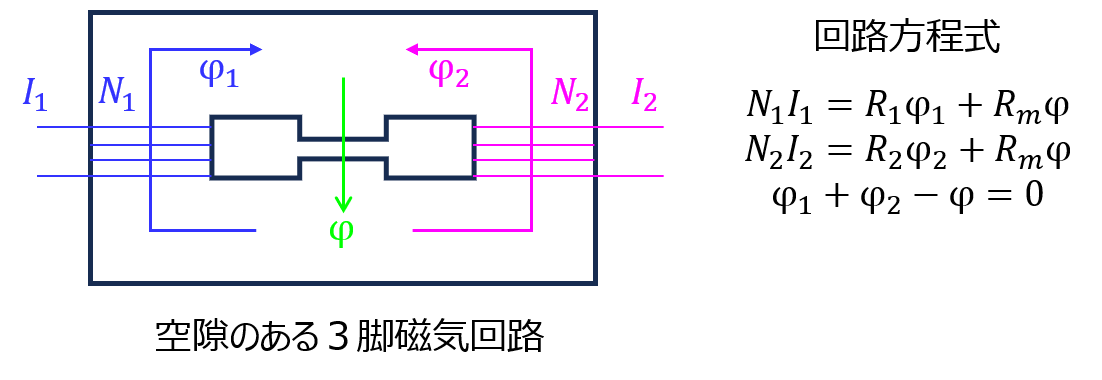
磁気回路
大学によっては出題されることがあります。過去に九大で取り上げられることがありました。
回路パラメータさえ定式化できれば、後は電気回路の計算です。
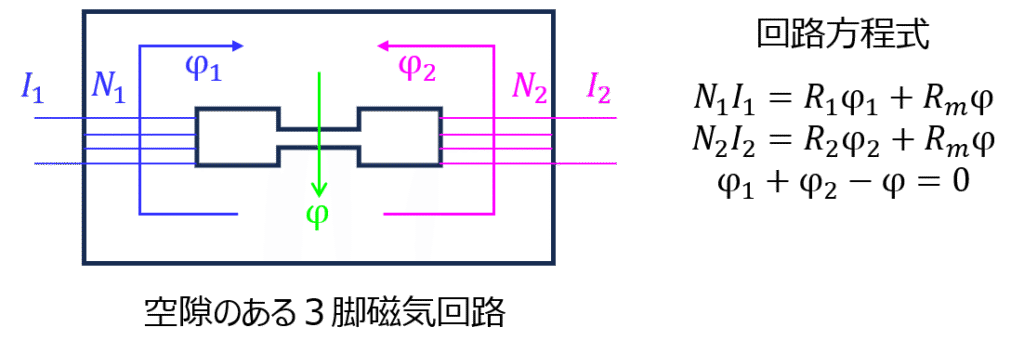
問題[29-1] 空隙のある環状鉄心の磁場 ☆☆★
対策になりそうな大学:九大
教科書によっては演習問題として紹介されています。オーソドックスな内容なので、知識の確認に使うと良いです。
問題[33] 空隙のある三脚コイルの磁場 ☆☆★
対策になりそうな大学:九大
問題29-1と同じです。磁路の長さが変わるため磁気抵抗の値が変わりますが、それ以外は通常の回路計算です。
磁界が電流におよぼす力
本分野、意外と院試で出題されやすいです。磁場を求めた後、電磁力の式を用いて力Fを求めることができることから、問題の分量調整に最適です。
また、電磁力に関する知識も同時に問うこともできるため、出題者側としては都合の良い分野です。
問題[37] 2本の導線にかかる力(無限長) ☆☆★
対策になりそうな大学:全般
電磁力の式\(F=BIL\)を覚えていれば解決します。高校物理、大学受験でも頻繁に出てくる式なので、馴染みのある方も多いのではないでしょうか。
一応、本問で知識確認すると良いです。
問題[38] 2本の導線にかかる力(有限長) ☆☆★
対策になりそうな大学:全般
有限長になったことから、磁場の式が少し複雑になりますが、行うこととしては問題37と変わりありません。
三角関数をミスなく積分していきましょう。
問題[42] 無限に広い平面に正対する無限長導体に電流が流れた時に発生する力 ☆☆☆
対策になりそうな大学:全般
鏡像法の応用版です。影像導体を境界面に対し等しい距離におきます。(電流の向きは逆)
その後はアンペールの法則を重ね合わせ、力を求めていきます。
最後に
次回は、8章電磁誘導の法則のオススメ問題を説明します。
大学によっては、8章までが試験範囲になっていることがあります。それ故、集大成のような問題が並びますが、演習としてはもう一息です。