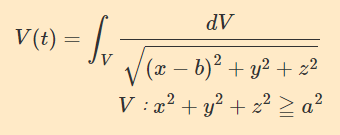下記の積分値を求めよ。ただし、\((a>0,b>0)\)とする。積分領域は式(2)で与えられる。
\begin{eqnarray}V(t)=\int _{V}\dfrac{dV}{\sqrt{\left( x-b\right) ^{2}+y^{2}+z^{2}}} \\ V: x^{2}+y^{2}+z^{2}\geqq a^{2}\end{eqnarray}
はじめに
本問は、複雑な計算になります。与えられた領域Vから極座標変換すると良いと考えられます。しかし、これだけでは定数\(b\)が残ります。続きの計算はどのように行うのでしょうか。
なお、同じ形式の問題が農工大で出題されたことがあります。同大学を志望する方は是非チェックしてください。
本記事で覚えたいこと
- 余計な文字が入っている場合でも、通常通り極座標変換する
- 場合分けを利用し、積分計算を分ける。
拍子抜けするCHECK項目で申し訳ありません。下記節のように、教科書で説明されている極座標変換することが、実はカギになります。
式(1)の\(\sqrt{}\)内に\((x-b)^{2}\)があるからと言って、\((x-b)=r\sin \theta\)と変換することはオススメしません。積分領域が煩雑になるからです。
一方で、\(x=r \sin \theta\)とおくと、領域は簡単になるものの式が難しくなります。どちらを取る話になりますが、後者の方が高校数学で経験のある計算に帰着できます。お勧めです。
ただし、計算結果に絶対値が付きますので、丁寧に場合分けすることが必要です。
極座標変換の方法
他サイトでもよく紹介されていますが、本サイトでも概要説明します。
\begin{eqnarray}x=r\cos \theta,y=r\sin \theta \cos \varphi , z=r\sin \theta \sin \varphi\end{eqnarray}とすると、ヤコビアン\(J\)は
\begin{aligned}\left| J\right| &=\begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta } & \dfrac{\partial x}{\partial \varphi } \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta } & \dfrac{\partial y}{\partial \varphi } \\ \dfrac{\partial z}{\partial r} & \dfrac{\partial z}{\partial \theta} & \dfrac{\partial z}{\partial \varphi } \end{vmatrix} \\ & =\begin{vmatrix} \sin \theta \cos \varphi & r\cos \theta \cos \varphi & -r\sin \theta \sin \varphi \\ \sin \theta \sin \varphi & r\cos \theta \sin \varphi & r\sin \theta \cos \varphi \\ \cos \theta & -r\sin \theta & 0 \end{vmatrix} \\ &=r^{2}\sin \theta\end{aligned}
積分領域は下記のようになる。
\begin{eqnarray}0\leq r\leq a,0\leq \theta \leq \pi ,0\leq \varphi \leq 2\pi\end{eqnarray}
解答例
前章により、式(1)を極座標変換する。
\begin{aligned}V\left( t\right) &=\int _{0}^{2\pi }d\varphi \int _{0}^{a}dr\int _{0}^{\pi }\dfrac{r^{2}\sin \theta d\theta }{\sqrt{\left( r\cos \theta -b\right) ^{2}+r^{2}\sin ^{2}\theta }} \\ &=2\pi \int _{0}^{a} r^{2} dr\int _{0}^{\pi }\dfrac{\sin \theta d\theta }{\sqrt{r^{2}-2rb\cos \theta +b^{2}}} \\ &=\dfrac{1}{rb} 2\pi \int _{0}^{a} r^{2} dr \left[ \sqrt{r^{2}-2rb\cos \theta +b^{2}}\right] ^{\pi }_{0} \\ &= 2\pi \int _{0}^{a} r^{2} dr\dfrac{1}{rb}(|r+b|-|r-b|)\end{aligned}
\(\sqrt{} \)内の式が難しくとも、積分できる形に帰着できました。
他の問題もこういったパターンが多いです。領域を工夫するより、計算を頑張りましょう。
ここから先は絶対値の値次第で結果が変わります。順に場合分けしていきます。
(i)\(b>a\)のとき、\(|r-b|<0\)だから
\begin{aligned}V(t)&=2\pi \int _{0}^{a} r^{2} dr \dfrac{1}{rb} 2r \\ &= 2 \pi \dfrac{2}{b}\int _{0}^{a} r^{2} dr \\ &= \dfrac{4 \pi a^{3}}{3b}\end{aligned}
(ii)\(b<a\)のとき
\begin{aligned} \dfrac{1}{rb}(|r+b|-|r-b|)= \begin{cases}\dfrac{2}{b}\left( 0\leq r\leq b\right) \\ \dfrac{2}{r}\left( b\leq r\leq a\right) \end{cases}\end{aligned}
を利用して
\begin{aligned}V(t) &= 2\pi \left( \int _{0}^{b}r^{2}\cdot \dfrac{2}{b}dr+\int ^{b}_{a}r^{2}\cdot \dfrac{2}{r}dt\right) \\ &=\dfrac{4\pi }{b}\left( \left[ \dfrac{r^{3}}{3}\right] _{0}^{b}+b\left[ \dfrac{r^{2}}{2}\right] _{a}^{b}\right) \\ &=2\pi a^{2}-\dfrac{2}{3}\pi b^{2}\end{aligned}
最後に
大学入試並みの計算量ですが、院試でもこのレベルがたまに出てきます。油断することなく、是非自分のものにしてください。