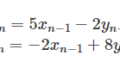固有ベクトルを用いた行列のn乗の計算

数学

2024.04.262024.07.14

行列\(A=\begin{pmatrix} -8 & 6 \\ -9 & 7 \end{pmatrix}\)が存在する。

固有値\(\lambda =-2,1\)で、対応する固有ベクトルは\(v_{1}\begin{pmatrix} 1 \\ 1 \end{pmatrix},v_{2}=\begin{pmatrix} 2 \\ 3 \end{pmatrix}\)である。

このとき、\begin{eqnarray}A^{n}\begin{pmatrix} 0 \\ 1 \end{pmatrix}\end{eqnarray}の値を求めよ。
新訂線形代数問題集P65 大問147 より抜粋

はじめに
本記事で覚えたいこと
解答例
最後に
参考文献

はじめに

本問は、固有値の性質を利用し、\(A^{n}\)の乗数を落としていき、結果を求める問題です。色々な大学でたまに出題されます。(電通大2023など)

まず自力で解けるか確認し、分からなかった場合は復習に役立てて下さると幸いです。

なお、問題は引用元から抜粋しましたが、解答は略解での記載でした。本記事で解答のキーポイントを埋め合わせできればと思います。

本記事で覚えたいこと

行列\(A\)の固有値を\(\lambda\)、対応する固有ベクトルを\(v_{1}\)とすると
\(Av_{i}=\lambda v_{i}\)が成立する。
ある2次元ベクトル\(a\)を固有ベクトル\(v_{1},v_{2}\)を使用して、\(a=sv_{1}+tv_{2}\)と分解する。
\(A^{n}a=sA^{n}v_{1}+tA^{n}v_{2}=s\lambda_{1}^{n}v_{1}+t\lambda_{2}^{n}v_{2}\)と変形し、結果を求める。

１．２．がキーポイントです。

１．は固有値の性質そのものですが、対角化などの問題を解くうえではあまり使用しません。ですので、盲点になりがちなところです。

２．は、一次独立なベクトルを組み合わせれば、同じ次元の任意のベクトルを表すことができる事実を知っているとできます。

文字ばかりで分かりづらいと思います。下記に解答例を示しますので、ご覧いただければと思います。

解答例

まず、\(\begin{pmatrix} 0 \\ 1 \end{pmatrix}=-2\begin{pmatrix} 1 \\ 1 \end{pmatrix}+\begin{pmatrix} 2 \\ 3 \end{pmatrix}\)とベクトルを分解できる。(CHECK2)

これより、求める式(1)は以下のように変形できる。

\begin{eqnarray}A^{n}\begin{pmatrix} 0 \\ 1 \end{pmatrix}=A^{n}\left( (-2)\begin{pmatrix} 0 \\ 1 \end{pmatrix}+\begin{pmatrix} 2 \\ 3 \end{pmatrix}\right)\end{eqnarray}

(CHECK1)の性質より

\(A\begin{pmatrix} 1 \\ 1 \end{pmatrix}=\left( -2\right) \begin{pmatrix} 1 \\ 1 \end{pmatrix},A\begin{pmatrix} 2 \\ 3 \end{pmatrix}= \begin{pmatrix} 2 \\ 3 \end{pmatrix}\)

だから、これをn乗分適用することで

\begin{aligned}A^{n}\begin{pmatrix} 0 \\ 1 \end{pmatrix}&=A^{n}\left( (-2)\begin{pmatrix} 0 \\ 1 \end{pmatrix}+\begin{pmatrix} 2 \\ 3 \end{pmatrix}\right) \\ &= -2\left( -2^{n}\right) \begin{pmatrix} 1 \\ 1 \end{pmatrix}+\begin{pmatrix} 2 \\ 3 \end{pmatrix}\\ &=\begin{pmatrix} \left( -2\right) ^{n+1}+2 \\ \left( -2\right) ^{n+1}+3 \end{pmatrix}\end{aligned}

であることが分かった。