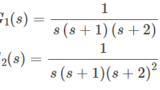\(A=\begin{pmatrix} 0 & 1 \\ -3 & -4 \end{pmatrix}\)の行列指数関数\(e^{At}\)を下記2つの方法で求めよ。
1.固有値を用いた対角化
2.ラプラス変換
はじめに
本問、意外と出題されたりします。現代制御での出題が最も多いですが、線形代数でも何かしらの初期値を与えて、そこからの時間変化をグラフに描く問題が出題されることがあります。
知っていれば得点できますので、是非この記事で復習いただければと思います。
本記事で覚えたいこと
固有値を用いた行列指数関数の求め方
- 行列\(A\)の固有値\(\lambda_{1},\lambda_{2}\)を求める
- 各固有値に対する固有ベクトル\(v_{1},v_{2}\)を求め、\(P=(v_{1},v_{2}) \)とする。
- \(P\)の逆行列\(P^{-1}\)を求める。
- \(D=\begin{pmatrix} e^{\lambda_{1}t} & 0 \\ 0 & e^{\lambda_{2}t} \end{pmatrix}とし、e^{At}=PDP^{-1}を求める。\)
行列\(A\)を対角化する作業とあまり変わりません。行列Dの部分が、exp項に変わったところに注意すれば、最終的に答えに行き着くのではないでしょうか。
ラプラス変換を用いた状態遷移行列の求め方
- 行列\((sE-A)\)の逆行列\((sE-A)^{-1}\)を計算する。
- 求めた逆行列を逆ラプラス変換し、状態遷移行列\(e^{At}\)を求める。
ひょっとすると、こちらのやり方のほうがシンプルかもしれません。
\(\dfrac{dx(t)}{dt}=Ax(t)\)をラプラス変換すると、\(sX(s)-x(0)=AX(s)\)となるため
\begin{eqnarray}(sE-A)X(s)=x(0) ⇔ X(s)=(sE-A)^{-1}x(0) ⇔ x(t)=e^{At}x(0)\end{eqnarray}
になることから、上記の手順(CHECK)が発生しています。
解答例
固有値を用いた場合
特性方程式\(|A-\lambda E|\)について
\begin{aligned}\begin{vmatrix} -\lambda & 1 \\ -3 & -4-\lambda \end{vmatrix} &=\lambda^{2}+4\lambda+3 =0 \\ \lambda&=-3,-1\end{aligned}
(i)\(\lambda=-3\)のとき、固有ベクトルは、\(v_{1}=\begin{pmatrix} -\frac{1}{3} \\ 1 \end{pmatrix}\)
(ii)\(\lambda=-3\)のとき、固有ベクトルは、\(v_{2}=\begin{pmatrix} -1 \\ 1 \end{pmatrix}\)
これより、\(P=\begin{pmatrix} -\frac{1}{3} & -1 \\ 1 & 1 \end{pmatrix},P^{-1}=\dfrac{1}{2}\begin{pmatrix} 3 & 3 \\ -3 & -1 \end{pmatrix}\)を得る。
よって、求める状態遷移行列\(e^{At}\)は
\begin{align}e^{At} &= \dfrac{1}{2}\begin{pmatrix} -\frac{1}{3} & -1 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} e^{-3t} & 0 \\ 0 & e^{-t} \end{pmatrix}\begin{pmatrix} 3 & 3 \\ -3 & -1 \end{pmatrix} \\ &= \dfrac{1}{2}\begin{pmatrix} -\frac{1}{3}e^{-3t} & -e^{-t} \\ e^{-3t} & e^{-t} \end{pmatrix}\begin{pmatrix} 3 & 3 \\ -3 & -1 \end{pmatrix} \\ &= \dfrac{1}{2}\begin{pmatrix} -e^{-3t}+3e^{-t} & -e^{-3t}+e^{-t} \\ 3e^{-3t}-3e^{-t} & 3e^{-3t}-e^{-t} \end{pmatrix}\end{align}
ラプラス変換を用いた場合
\((sE-A)=\begin{pmatrix} s & -1 \\ 3 & s+4 \end{pmatrix}\)だから、これの逆行列は
\begin{align}(sE-A)^{-1}&=\dfrac{1}{s^{2}+4s+3}\begin{pmatrix} s+4 & 1 \\ -3 & s \end{pmatrix} \\ &=\dfrac{1}{2}\begin{pmatrix} -\frac{1}{s+3}+\frac{3}{s+1} & -\frac{1}{s+3}+\frac{1}{s+1} \\ \frac{3}{s+3}-\frac{3}{s+1} & \frac{3}{s+3}-\frac{1}{s+1} \end{pmatrix} \end{align}
よって、逆ラプラス変換することで、行列指数関数
\begin{eqnarray}e^{At}= \dfrac{1}{2}\begin{pmatrix} -e^{-3t}+3e^{-t} & -e^{-3t}+e^{-t} \\ 3e^{-3t}-3e^{-t} & 3e^{-3t}-e^{-t} \end{pmatrix}\end{eqnarray}
を得る。
最後に
参考文献(P22)にあるように、微分方程式を分解し、行列指数関数を求める第3の方法もあります。ただ、手計算で行うには大変でしたので、今回は割愛します。興味がある方は是非チェックしてください。
また、ラプラス変換を使用した方法の途中で、部分分数分解を行った計算があります。効率的に部分分数分解する方法を下記のページで紹介しています。宜しければチェック下さると幸いです。