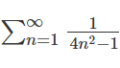実数\((x,y)\)が以下の領域\(D_{1},D_{2}\)を取るとき、それぞれの積分結果\(F_{1},F_{2}\)を求めよ。
\begin{align}&D_{1}=\{ \left( x,y\right) :x\geq 0,y\geqq 0,x+y\leqq \dfrac{\pi }{2}\} \\ &F_{1}=4\iint _{D_{1}}\left( x-y\right) \exp \left( \dfrac{\left( x-y\right) ^{2}}{x+y+1}\right) \\ &D_{2}=\{ \left( x,y,z\right) :0≦ x+y≦2 , 0≦y+z≦3 , 0≦z+x≦4\} \\ &F_{2}= \iiint _{D}dxdydz \end{align}
はじめに
重積分は、解析学を試験範囲とする大学の院試で頻出分野です。
様々な問われ方がありますが、基本的な解法として、以下の方針をまず考えます。
- 積分範囲を別の変数で置き換えて、手計算で積分可能な数式に変換
- それぞれの積分変数の取りうる範囲を整理し、手計算で積分可能な領域を導く
今回は、前者(別の変数で置き換える方法)について取り上げます。
極座標変換による積分
最も有名な変数の変換として、\(0≦x^{2}+y^{2}≦1\)の領域の面積を求めるとき
\begin{split}x=r\cos \theta , y=r\sin \theta , (0≦r≦1) , (0≦\theta≦2\pi)\end{split}
と極座標変換する方法があります。
ヤコビアン\(J=\begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta } \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta } \end{vmatrix}=\begin{vmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{vmatrix}=r\) より
\begin{split}\iint _{S}dxdy=\int ^{1}_{0}rdr\int ^{2\pi }_{0}d\theta =\pi \end{split}
と、半径1の円の面積を求めることができました。
こちらに関しても今後詳しく扱いたいですが、今回は他の変換方法を取り上げます。
対称式型の変数変換
冒頭の問題を解く際に使用する変数変換方法です。
対称式のブロック毎に一つの変数で置き換えると、積分しやすい形に変換できることが多いです。
有名問題ではありますが、ネット検索してもあまりヒットしないように感じます。
ご存じではない方は、本問を通して、積分計算する際の引き出しが増えると幸いです。
解答例\(F_{1}\)
\(x=\dfrac{u+v}{2},y=\dfrac{u-v}{2}\)より、ヤコビアン\(J\)は
\begin{align}J&=\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial n} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} \\ &= \begin{vmatrix} \dfrac{1}{2} & \dfrac{1}{2} \\ \dfrac{1}{2} & -\dfrac{1}{2} \end{vmatrix} \\ &= \dfrac{1}{2}\end{align}
積分範囲は、以下のように書き直せる。
\(x≧0,y≧0 \)より、\(0≦x+y≦\dfrac{\pi}{2} \Leftrightarrow 0≦u≦\dfrac{\pi}{2} \)
uを固定すると、\(x=\dfrac{u+v}{2},y=\dfrac{u-v}{2}\)と\(x≧0,y≧0\)より
\(x=0\)のとき\(v=-u\)、\(y=0\)のとき\(v=u\)で、\(v\)の取りうる値の上下限が求められる。\(-u≦v≦u\)
\(u\)を先に積分するとき、\(u=x+y\)より、\(x=0\)のとき、\(-u≦y≦u\)
これより、関数\(F\)は以下のように計算できる。
\begin{align}F&=4\iint _{D}\left( x-y\right) \exp \left( \dfrac{\left( x-y\right) ^{2}}{x+y+1}\right) \\ &= 4\int _{0}^{\frac{\pi }{2}}du\int ^{u}_{-u}v\exp \left( \dfrac{v^{2}}{u+1}\right) \frac{1}{2} dv \\ &= \int ^{\frac{\pi }{2}}_{0}\left[ \exp \dfrac{v^{2}}{u+1}\right] ^{u}_{-u}du \\ &=0 \end{align}
解答例 \(F_{2}\)
3変数でも、前章で説明した方針は変わりません。
\(x+y=s,y+z=t,z+x=u\)とおくと、以下の積分領域に変換できる
\begin{split}\begin{aligned}D=\{ \left( s,t,u\right) :0≦s≦2 , 0≦t≦3 , 0≦u≦4\} \end{aligned}\end{split}
\begin{eqnarray} \left\{ \begin{array}{l} x=\frac{s-t+u}{2} \\ y=\frac{s+t-u}{2} \\ z=\frac{-s+t+u}{2}\end{array} \right. \end{eqnarray}
と整理でき
ヤコビアン \begin{split}J=\begin{vmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} & \frac{\partial x}{\partial u} \\ \frac{\partial y }{\partial s} & \frac{\partial y}{\partial t} & \frac{\partial y}{\partial u} \\ \frac{\partial z}{\partial s} & \frac{\partial z}{\partial t} & \frac{\partial z}{\partial u} \end{vmatrix}=\begin{vmatrix} \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{vmatrix}&=\frac{1}{2}\end{split} であるので
以下の積分領域に変換できる
\begin{split}V=\iiint _{D}dxdydz=\int ^{2}_{0}ds\int _{0}^{3}dt\int ^{4}_{0}du\cdot \frac{1}{2}\end{split}
これを計算すると、求める体積\(V\)は
\begin{split}V=\frac{1}{2}\cdot 2\cdot3\cdot4=12\end{split}
最後に
高校数学では、1変数を固定し、残りの変数の取りうる範囲を調査、積分することがセオリーでした。
今回紹介したヤコビアンを使用しての積分は、大学数学ならではの方法です。
電通大頻出分野になっています。志望される方は、是非類題経験を積むと良いかもしれません。