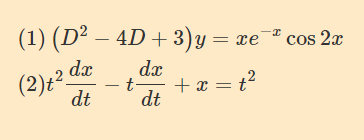演算子法を用いた微分方程式の例題

下記の微分方程式を演算子法を用いて解け。
$$\begin{array}{}\text{(1)}& \begin{array}{rl}& (1)(D^2-4D+3)y=x{e}^{-x}\cos 2x\\ & (2)t^2{\displaystyle \frac{dx}{dt}}-t{\displaystyle \frac{dx}{dt}}+x=t^2\end{array}\end{array}$$

はじめに

微分方程式を演算子を用いて解きます。

$y^{\prime }=e^{ax}$と置いて解く方法が一般的ですが、他サイト様で多数取り扱っています。

そこで、本サイトでは、あえて演算子を使うことで解いてみます。試験本番では、解きやすい方法で解くことをオススメします。

本記事で覚えたいこと

結局、一般解を求め、そこから特殊解を足し合わせた結果が微分方程式の解であることは変わりありません。

$y=\exp ax$項に置き換え、解を求めていた一連の操作を演算子を用いてシステマティックにしたに過ぎません。

(1)の右辺は少し複雑ですが、部分分数分解など使用し、解くことができます。

(1)の右辺には$\cos$項があります。これは$Re(\exp )$と置き換えることで、$\exp$項に帰着できます。これを用いて、４．を利用します。

しかし、(2)はそのままでは解くことができません。微分項の係数に変数$x$がかけられているからです。オイラー型の微分方程式と言います。

これは、$y=\log t$と置き換えることで、微分項の係数は定数のみに置き換えることができます。

解答例

(1)右辺が複雑な微分方程式

まず、一般解を求める。(右辺)=0とし

$$\begin{array}{}\text{(2)}& \begin{array}{r}(D-1)(D-3)y=0,D=1,3\end{array}\end{array}$$

これより一般解は、$C_1{e}^x+C_2{e}^{3x}$

次に、(左辺)のD項を割ったときの(右辺)

${\displaystyle \frac{1}{D^2-4D+3}}x{e}^{-x}\cos 2x$を考える。微分の関係により

$$\begin{array}{}\text{(3)}& \begin{array}{rl}(1)& =x{\displaystyle \frac{1}{D^2-4D+3}}{e}^{-x}\cos 2x-{\displaystyle \frac{2D-4}{(D^2-4D+3{)}^2}}{e}^{-x}\cos 2x\\ & =xRe{\displaystyle \frac{e^{(-1+2i)x}}{{(-1+2i)}^2-4(-1+2i)+3}}–Re{\displaystyle \frac{2D-4}{({(-1+2i)}^2-4(-1+2i)+3{)}^2}}{e}^{(-1+2i)x}\\ & =xRe{\displaystyle \frac{e^{(-1+2i)x}}{4-12i}}-Re(2D-4){\displaystyle \frac{e^{(-1+2i)x}}{{(4-12i)}^2}}\\ & ={\displaystyle \frac{x}{4}}Re{\displaystyle \frac{e^{(-1+2i)x}}{1-3i}}+{\displaystyle \frac{1}{16}}pe(D-2){\displaystyle \frac{(4-3i)e^{(-1+2i)x}}{25}}\\ & ={\displaystyle \frac{x}{40}}Re(1+3i)e^{(-1+2i)x}+{\displaystyle \frac{1}{400}}Re(17i-6)e^{(-1+2i)x}\\ & ={\displaystyle \frac{x{e}^{-x}}{40}}(\cos 2x+3\sin 2x)-{\displaystyle \frac{e^{-x}}{400}}(6\cos 2x+17\sin 2x)\end{array}\end{array}$$

と特殊解を求めることができた。

以上より、求める微分方程式の解は

$$\begin{array}{}\text{(4)}& y=C_1{e}^x+C_2{e}^{3x}+{\displaystyle \frac{x{e}^{-x}}{40}}(\cos 2x+3\sin 2x)-{\displaystyle \frac{e^{-x}}{400}}(6\cos 2x+17\sin 2x)\end{array}$$

(2)オイラー型微分方程式

$y=\log t$と置くと

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\displaystyle \frac{dx}{dt}}& ={\displaystyle \frac{dy}{dt}}\cdot {\displaystyle \frac{dx}{dy}}\\ & ={\displaystyle \frac{1}{t}}\cdot {\displaystyle \frac{dx}{dy}}\end{array}\end{array}$$

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\displaystyle \frac{d^{2}y}{d{t}^2}}& ={\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{dt}{dt}}\right)\\ & ={\displaystyle \frac{d}{dt}}({\displaystyle \frac{1}{t}}\cdot {\displaystyle \frac{dx}{dt}})\\ & ={\displaystyle \frac{1}{t^2}}({\displaystyle \frac{d^{2}x}{d{y}^2}}-{\displaystyle \frac{dx}{dy}})\end{array}\end{array}$$

式(5)(6)を与式に代入し

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{d^{2}x}{d{y}^2}}-2{\displaystyle \frac{dx}{dy}}+x=e^{2y}\end{array}$$

これを微分演算子に置き換えて

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& D^2-2D+1=e^{2y}\\ & {(D-1)}^2=e^{2y}\end{array}\end{array}$$

(右辺)=0とすると、$D=1$(重解)

よって、一般解は、$C_1{e}^y+C_{2}y{e}^y$とおける。

次に特殊解を求める。$\exp$項は$2y$なので、$D=2$を代入すれば良いので

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{e^{2y}}{(D-1{)}^2}}=e^{2y}\end{array}$$

以上より、求める微分方程式の解は

$$\begin{array}{}\text{(10)}& \begin{array}{rl}x(y)& =C_1{e}^y+C_{2}y{e}^y+e^{2y}\\ x(t)& =(C_1+C_2\log t)t+t^2\end{array}\end{array}$$

最後に

演算子法を用いれば、決まったルールに基づいて楽に解を求められることがあります。(2)は、北大での出題が多いため、同大学を志望する方は是非参考に下さればと思います。