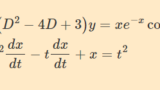【九州大学大学院】システム情報学府 院試対策(数学)

数学の試験範囲

線形代数、解析学、ベクトル解析、確率統計からなります。線形代数、解析学は必須選択で、ベクトル解析、確率統計のうち1題選択です。

昔は微分方程式、複素関数論がそれぞれ独立した大問になっていましたが、解析学と統合。情報論理学もありましたが、廃止されたようです。

九大 システム情報学府 院試の全体

電気電子工学専攻、情報理工学専攻と分かれています。数学は両者ともに同じ分野、選択範囲になっており、専門科目に違いがあります。

制御工学については、専門科目に属しています。電気電子工学専攻のみ選択可能です。

全体的な難易度ですが、複素関数論などが独立した大問だった頃と比較して易しくなったと思います。特に、解析学が顕著です。微分方程式、複素関数論が小問としての出題になったことから、深堀する問題が出なくなりました。

よって、出題範囲は広くなれど、易化しています。教科書レベルの問題をマスターすることで、ある程度の点数が見込めるのではないかと思います。

本セットでは、線形代数が難しいです。巷の大学でよくある固有値からの対角化はあまり出題されず、漸化式を行列表示に帰着して解く。線形独立に関する計算、証明問題が多いです。他の大学で勉強しているから大丈夫！と高を括っていると痛い目に遭いそうです。

ベクトル解析と確率統計は同じくらいの難易度だと思います。得意な方を選択する戦法で良いと思います。

ベクトル解析は、線積分、法線ベクトルの求め方。確率統計は、条件付き確率の問題が多いです。どちらも、一般的な問題集でよく出題されています。奇をてらった勉強は必要ありません。

全体

最近5年分は以下の分野の出題がありました。

バリエーションが多いですが、分野別に見ていきます。

線形代数：前章で説明した内容と同じです。他大学と傾向が違いますが、問題文に詳しく誘導が書かれています。その通りに解いていく愚直さが求められます。

解析学：これは他大学とあまり変わりません。極値の判定、テイラー展開など、様々な大学で出題されます。高校数学の延長で解けることも多いので、是非取りたいです。珍しく、他大学では頻出の重積分があまり出てきません。

微分方程式：同次系微分方程式など、基本的な方程式が出題されます。たまに、4階の微分方程式が出題されることもあります。(他大学ではあまり見ません。)解き方が分からないときは丸々落としかねないので、問題集で網羅的に演習する方が良いです。

複素関数：基本的に、ある積分路内の孤立特異点の留数を取る問題が多いです。以前は、写像(複素数平面)の出題がありました。最近時は小問一つ分のため、そこまで難しい問題は出ないと思います。満点を取る場合は対策したいです。

ベクトル解析：前章で説明した通りの内容が実際に出題されています。

確率統計：基本的に前章で説明した通りの内容ですが、連続確率密度関数の問題が出題されることがあります。他大学でもよく見る問題のため、併願先と一緒に対策すると良いです。

・対策に役立ちそうな本サイトの記事 (是非ご覧ください)

教科書(線形代数)

一般教養科目のため、統一した教科書が無いです。他の大学にも言えることですが、自身のお持ちの教科書で問題無いと思います。ここでは、問題集だけ紹介します。

線形代数 (大学院入試問題から学ぶシリーズ)　佐藤信哉 (著)

証明問題のように、理学部っぽい問題も取り扱っているため、九大の傾向と合いそうです。第1章の行列の計算までやりこむ必要は無いですが、頻出分野を中心に勉強すると良いです。

解析学、微分方程式

こちらも一般教養科目です。ご自身のお持ちの本での勉強で良いと考えます。同じく、問題集を紹介します。

解析演習 (数学演習ライブラリ 2) 野本 久夫 (著), 岸 正倫 (著)

線形代数と同じことが言えますが、極値の計算、偏微分などの頻出分野を中心に勉強すると良いです。あとは過去問で補強して、足りないところを随時補っていくイメージです。

演習微分方程式 (演習数学ライブラリ 新版 3) 寺田 文行 (著), 坂田 ひろし (著)

名古屋大学と同じ本を紹介しますが、九大にもオススメできます。と言いますか、微分方程式の対策はこちらの問題集でどの大学も対応できると考えています。前半の章に、院試頻出問題が集まっています。こちらを中心に勉強すると、見たことない微分方程式を院試本番で出くわすことが無くなるでしょう。

複素関数

ここからが専門科目です。シラバスに載っている本を紹介していきます。

工学系学生のための 複素関数攻略への一本道　板垣 正文 (著)

森北出版なだけあり、分かりやすく解説しています。まだ複素関数論の本をお持ちではない方は、九大志望でなくともオススメします。

ただ、たまに出題される写像に関する説明が豊富かと言うと、そうではないです。他の本でも同じですので、ここだけはネットで検索するなりして自分なりの理解を深めていく必要がありそうです。

ベクトル解析

ベクトル解析とフーリエ解析 柁川 一弘 (著), 金谷 晴一 (著) (シラバス対象本)

前半部分でベクトル解析について解説しています。例題、演習問題ともに適切な分量ですが、ベクトル解析の問題は一般的な設問が多いです。どうしてもこの本で無いとダメな部分は見当たらないため、ご自身のお持ちの本で代用は効くと考えます。

確率統計

スッキリわかる確率統計 皆本 晃弥 (著) (シラバス対象本)

定理の証明については事細かに述べられていますが、演習問題が略解程度しかないことが気になります。結局、自身で分からない範囲について調べる時間が余計にかかることを勘案した上で購入すると良いです。

頻出分野の条件付き確率に関する説明も特別充実しているわけではないので、お持ちの参考書でも代用できると思います。

対策に使える他大学の問題

少し独特な問題もあるので、全てオススメできるわけではないです。実際に確認し、使えると判断した問題を演習すると良いです。

線形代数は、東工大の問題が傾向的に似ています。九大からするとオーバーワークかもしれませんが、一度覗いてみると良いかもしれません。

解析学、微分方程式：傾向が変わらないため、どこの大学でも良いと思います。

複素関数：神戸大がオススメです。ある積分路内の孤立特異点の留数を取る問題が多いためです。

ベクトル解析は、北大以外出題しているところを見ていません。市販の問題集で良いと思います。

確率統計は、強いて言えば広島大です。条件付き確率の問題に絞って演習すると良いです。

最後に

九大院試の数学は、他大学と比較して幅広い勉強が求められます。難しい問題を解く前に、様々な分野の問題に手を付ける勉強をする方が良いと思います。

勉強した暁には、他大学を併願したときに数学選択科目で困ることは無くなるでしょう。