【制御工学】位相進み補償の考え方、原理と例題

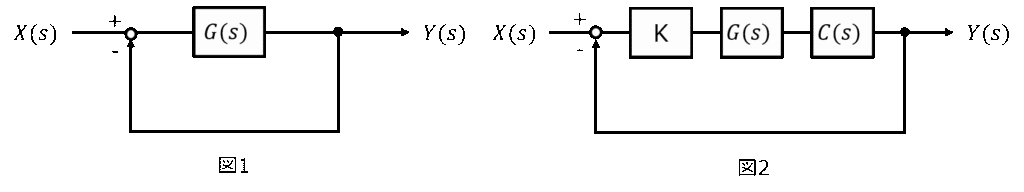
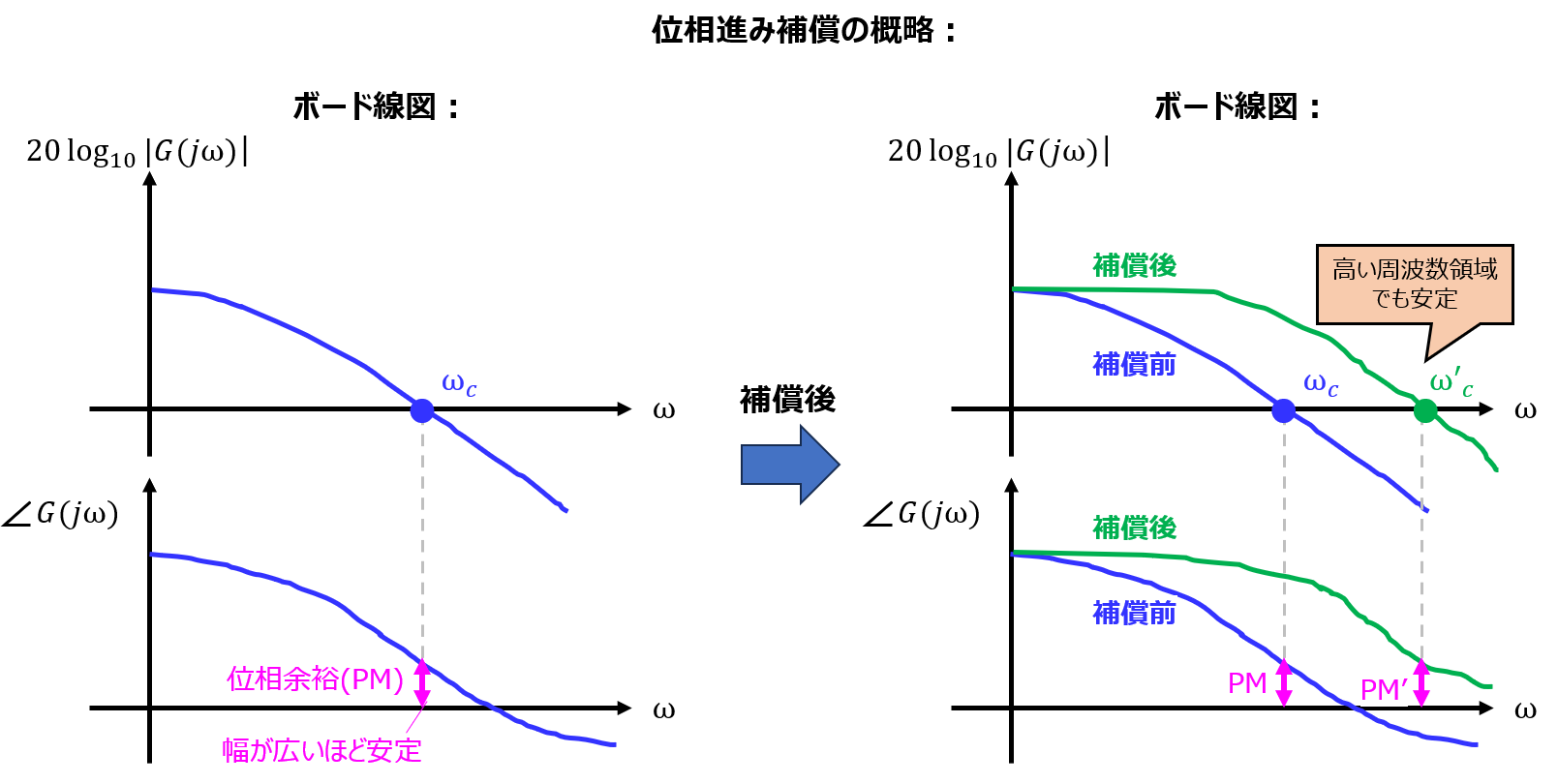
位相進み補償とは

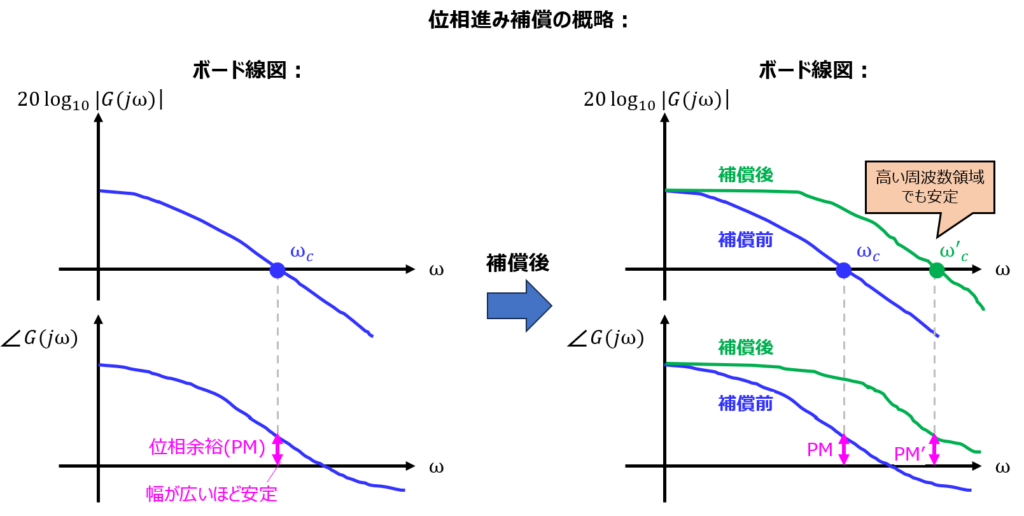
ゲイン交差周波数付近の位相を進めて、位相余裕を増やすことを言います。

以前の記事で位相余裕の考え方について説明しました。

開ループ伝達関数\(G(j\omega)\)のゲイン[dB]が0になるときのゲイン交差周波数\(\omega_{m}\)に対する位相が、-180度から離れている程度を言います。

実際、制御設計を進めていると、与えられた伝達関数の位相余裕がイマイチである場合があります。

例えば、ある伝達関数のゲイン交差周波数に対する位相が-180度の時、位相余裕は0になります。

少しでも外乱を受けると、位相が-180度以上になりたちまち発散します。

こういった事象を防ぐため、システムにある程度の位相余裕を持たせる必要があります。

では、どうすれば良いのか？答えは、図2のように位相進み要素をシステムに組み込めば良いです。

システムの位相余裕が大きくなり、安定性が改善します。

解答例

(1)ゲイン交差周波数とその時の位相余裕

ゲイン交差周波数

伝達関数\(G(s)\)を周波数領域\(G(j\omega)\)に落とす。

\(|G(j\omega)|=1\)のとき、ゲイン\(20\log|G(j\omega)|=0\)となり、これを与える\(omega\)がゲイン交差周波数\(\omega_{m}\)である。

\begin{aligned}G(j\omega)&=\dfrac{20}{j\omega(-\omega^{2}+4j\omega+5)} \\ &=\dfrac{20}{-4\omega^{2}+j\omega(5-\omega^{2})} \end{aligned}

\begin{aligned}|G(j\omega)|=\dfrac{20}{\sqrt{16\omega^{4}+\omega^{2}(5-\omega^{2})}}=1\end{aligned}

\begin{aligned}20=\sqrt{16\omega^{4}+\omega^{2}(5-\omega^{2})}\end{aligned}

これを解くと、求めるゲイン交差周波数は、\(\omega_{m}=\sqrt{5}\)

位相余裕

\(\omega_{m}=\sqrt{5}\)を\(G(j\omega)\)に代入すると、(1)式より

\begin{aligned}G(j\omega_{m})=-1\end{aligned}

よって、この時の位相は、\(\angle G(j\omega_{m})=-\pi \)

求める位相余裕は、\(PM=\pi+\angle G(j\omega_{m})=0\)

以上より、システムとして安定限界であることが分かった。

(2)位相進み補償

図2の伝達関数全体の位相特性を考える。図1に対し、\(C(j\omega)\)が追加されたので

\begin{aligned}\angle G(j\omega_{m})C(j \omega_{m})&=\pi+\angle G(j\omega_{m})+\angle C(j\omega_{m}) \\ &=\angle C(j\omega_{m}) \\ &=\tan^{-1}(\omega_{m} c T)- \tan^{-1}(\omega_{m} T) \end{aligned}

\(\omega_{m}=\dfrac{1}{T\sqrt{c}}\)なので、

\begin{aligned} (5)&=\tan^{-1}(\sqrt{c})-\tan^{-1}\left(\dfrac{1}{\sqrt{c}}\right)\end{aligned}

三角関数の公式

\begin{aligned}\tan(a+b)=\dfrac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}\end{aligned}を用いて

\begin{aligned}(6) &= \tan^{-1}\left(\dfrac{\sqrt{c}-\frac{1}{\sqrt{c}}}{1+\sqrt{c}\frac{1}{\sqrt{c}}}\right) \\ &= \tan^{-1}\left(\dfrac{c-1}{2\sqrt{c}}\right) \end{aligned}

これが位相余裕\(\frac{\pi}{6}\)になれば良いので

\begin{gather}\tan^{-1}\left(\dfrac{c-1}{2\sqrt{c}}\right)=\dfrac{\pi}{6} \\ \dfrac{c-1}{2\sqrt{c}} = \dfrac{1}{\sqrt{3}} \\ c=3 \end{gather}

\(\omega_{m}=\sqrt{5}\)のとき、ゲインが0[dB]になれば良いので

\begin{aligned}20\log |K|+20\log|G(j\omega_{m})|+20\log|C(j \omega_{m})|=0\end{aligned}

(1)より、\(20\log|G(j\omega_{m})|=0\)

\begin{aligned}|C(j \omega_{m})| &= \sqrt{\dfrac{1+\omega_{m}^{2}c^{2}T^{2}}{1+\omega^{2}T^{2}}} \\ &=\sqrt{\dfrac{1+c}{1+\frac{1}{c}}} \\ &=\sqrt{3}\end{aligned}

だから、\(K\)は(13)式を相殺するように設定すればよく

\begin{aligned}K=\dfrac{1}{\sqrt{3}}\end{aligned}

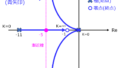
補足：位相進み補償後の根軌跡について

(2)より、位相進み要素をシステムに組み込むことで、位相余裕を確保することができました。

と言うことは、伝達関数の極の実部は正から遠のいていることが考えられます。実際、根軌跡としてどのように変化しているのか、確認しましょう。

伝達関数\(H(s)=\dfrac{K}{s(s+a)}\)に位相進み要素\(P(s)=\dfrac{s+c}{s+b}\) \((c<b)\)を組みこんだとき、下記のようになります。

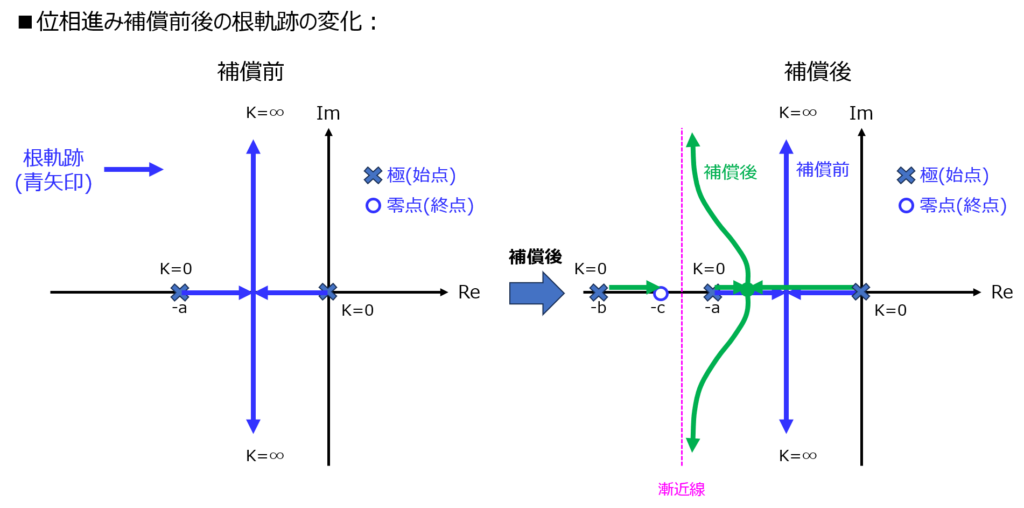
確かに、極の軌跡が正の実軸から遠ざかったことが分かりました。

※詳細な導出については、過去の記事を参照し、各自でよろしくお願いします。

最後に

位相補償に関する問題は、数々の大学の院試で出題されます。

是非、本問は解けるようになるまで繰り返してみてください。