詳解電磁気学演習のオススメ問題一覧 (3章)

はじめに

本記事は、前回の記事の続きです。

詳解電磁気学演習は、多数の問題が収録されており、電磁気学の勉強をする上で必ず持っておきたい本です。

一方で、「全部解くことはできないため、試験で出てきそうな問題を解きましょう。」と本サイト、他者様問わず、よく説明しています。

院試勉強を始めた段階だと、具体的にどのような問題が頻出なのか判断付かないと思います。

そこで、本サイトでは、是非とも解いておきたい問題を章ごとに紹介しています。

詳解電磁気学演習の章立て

問題のレベル分け

「院試に出てくる問題」及び「院試問題を解くために必要な知識を習得する問題」という観点で紹介しますが、どうしても問題のレベルは存在します。

そこそこ勉強している方に基礎問題の紹介しても仕方ないと考えますので、3段階で分けることにします。

☆★★：基礎(高校レベル)
☆☆★：標準(大学講義レベル)
☆☆☆：応用(院試レベル)

オススメ問題

3章：誘電体中の静電界

誘電体中の静電界

2章と同様院試頻出です。

誘電体になったので、真空中の誘電率ε0をεに置き換えるだけで済む問題もある一方、

\begin{aligned}\boldsymbol{D}=ε_{o}\boldsymbol{E}+\boldsymbol{P}\end{aligned}

のように、分極ベクトル\(\boldsymbol{P}\)を用いて定義から解く問題も多いです。(下記例)

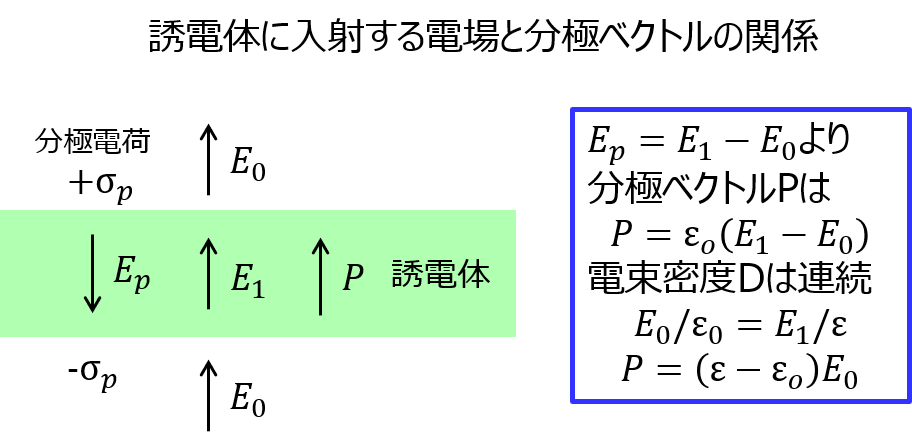
また、解答には境界条件の知識も必要不可欠です。

それぞれ紹介していきます。

問題[1] 誘電体板面に現れる分極電荷　☆☆★

対策になりそうな大学：神戸大、大阪公立大

境界条件を重視する大学で好んで出されそうです。

上記2つの大学が特にそうです。問題1だからと侮らずに、是非確認してみてください。

問題[2]分極電荷から発生する電場　☆☆★

対策になりそうな大学：神戸大、大阪公立大

問題1の類題です。(1)(2)だけでも確認すると良いです。

(3)(4)はやや複雑な系ですので、院試としては出ないかもしれません。

問題[4]誘電体に入射する波の屈折　☆☆★

対策になりそうな大学：神戸大、大阪公立大

境界条件により、誘電体中の電界を求めます。

電場は接線成分が連続、電束密度は法線成分が連続です。

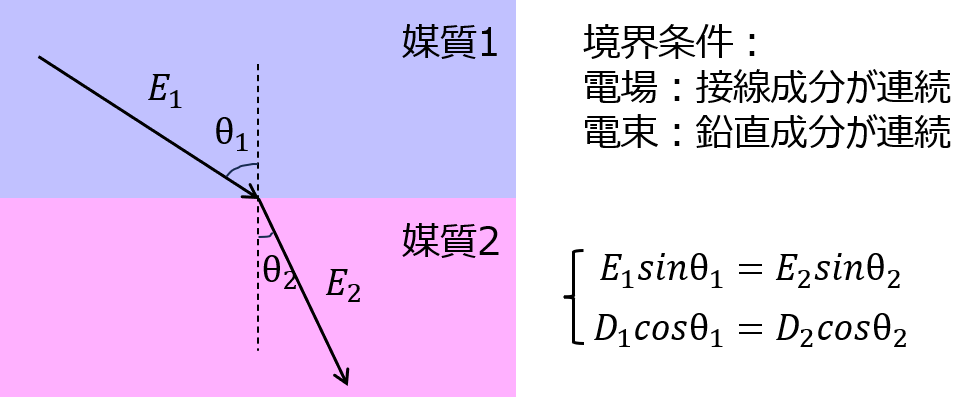
問題[5]境界条件の導出　☆☆★

対策になりそうな大学：阪大、東北大、神戸大、大阪公立大など全般

この問題は必須で確認した方が良いです。

教科書で説明されている内容ですが、院試での出題もあります。是非、自分のものにしましょう。

問題[6]位置によって誘電率が変わる誘電体　☆☆★

対策になりそうな大学：東大、阪大

こんな誘電体現実存在するのか・・？という気はしますが、特定の大学の院試で良く出てきます。

電位差を求める際、誘電体も変数を持っていることに注意して積分します。

問題[7,7-1]境界面の分極電荷　☆☆★

対策になりそうな大学：全般

問題5と同じくらい重要です。

真電荷、分極電荷の区別が付いていないと正しく解答できません。

また、異なる媒質の電荷を足し合わせると、境界面の電荷になります。

問題[10-2]誘電体球殻が入ったコンデンサの電位　☆☆★

対策になりそうな大学：全般

院試だけではなく、定期テストでも出てきそうな問題です。

電束密度は境界面の垂直成分に連続であることを利用します。

電荷分布を正確に書くことができれば、後は電束密度に関するガウスの法則で答えが出せます。

問題[11-2]異なる3つの誘電体で満たされた球殻コンデンサの電位　☆☆★

対策になりそうな大学：全般

問題[10]と同じ解き方です。類題演習にどうぞ。

問題[16-1]異なる2つの媒質を分割して球殻コンデンサに挿入したときの静電容量　☆☆★

対策になりそうな大学：全般

電場が連続になることから、静電容量は足し合わせることができます。

円筒形であるため、最初は気づきにくいです。

しかし、分かってしまえば高校物理の計算で解くことができます。

誘電体でのエネルギーと力

・力を積分するとエネルギー
・エネルギーを微分すると力

以上の関係は、力学だけでなく電磁気でも成立します。

本章は、この関係を利用すると解決する問題が多いです。

問題[26] マクスウェルの応力　☆☆★

対策になりそうな大学：東北大

仮想変位を考えたとき、かかる仕事から力を求めます。

境界面に対し垂直の場合、平行の場合の2通り練習しましょう。

問題[27-1] 導体球の周りを誘電体で包んだ時の静電エネルギー　☆☆★

対策になりそうな大学：全般

今まで紹介してきた問題と特にやることは変わりません。

静電エネルギー\(U=\frac{1}{2}QV\)を使用します。

\(V\)だけ、真空中の誘電率\(\varepsilon_{o}\)が誘電体の\(\varepsilon\)に変わるだけです。

問題[31] 円筒コンデンサの媒質間にかかる力　☆☆☆

対策になりそうな大学：九大

これは誘導が無いと難しいかもしれません。単位面積の電荷から発生する力を球殻全体で積分していきます。

境界面に対し垂直な成分に分解し積分していくことで答えにたどり着きます。

問題[32] 平板コンデンサの誘電体板にかかる力　☆☆★

対策になりそうな大学：全般

2章の金属板の場合とやることは変わりません。

誘電率を\(\varepsilon_{o}\)から\(\varepsilon\)に置き換えるだけです。

特殊な誘電体

特にオススメする問題はありません。

最後に

2章の真空中の静電界と重複する問題もありますが、分極電荷の問題を中心に演習することをオススメします。