詳解電磁気学演習のオススメ問題一覧 (2章)

はじめに

本記事は、前回の記事の続きです。

詳解電磁気学演習は、多数の問題が収録されており、電磁気学の勉強をする上で必ず持っておきたい本です。

一方で、「全部解くことはできないため、試験で出てきそうな問題を解きましょう。」と本サイト、他者様問わず、よく説明しています。

院試勉強を始めた段階だと、具体的にどのような問題が頻出なのか判断付かないと思います。

そこで、本サイトでは、是非とも解いておきたい問題を章ごとに紹介しています。

詳解電磁気学演習の章立て

問題のレベル分け

「院試に出てくる問題」及び「院試問題を解くために必要な知識を習得する問題」という観点で紹介しますが、どうしても問題のレベルは存在します。

そこそこ勉強している方に基礎問題の紹介しても仕方ないと考えますので、3段階で分けることにします。

☆★★：基礎(高校レベル)
☆☆★：標準(大学講義レベル)
☆☆☆：応用(院試レベル)

オススメ問題

2章：真空中の静電界

真空中の導体系

電位係数を扱った問題が多いです。多くの大学での院試では出てくることが少ないため、志望大学で出題されたことが無ければスルーでも良いかもしれません。

ただ、一部の大学(東北大、九大)では出題されたこともあります。

そういった需要も踏まえ、取り上げていきます。

どれも難しいので☆☆☆が多いです。

問題[4-1] 球殻内に電荷を置いた時、誘導される電荷　☆☆☆

対策になりそうな大学：九大

いきなり難しい問題です。多分、初見では誰も解けないと思います。

まずは、解答内容を理解し、その後自分で解けるか確認する方が良いと思います。

問題[4-2] 球殻内に電荷を置いた時、誘導される電荷　☆☆☆

対策になりそうな大学：九大

4-1の類題として練習すると良いと思います。

問題[6] 導体同士を接触したときの電荷を電位係数で表す　☆☆☆

対策になりそうな大学：九大

これも類題経験が無いと厳しいです。初見はすぐに解答を見て良いと思います。

問題[7] 第1導体、第2導体間の静電容量を電位係数で表す　☆☆☆

対策になりそうな大学：九大

電位係数の方程式に\(Q_{1}=Q,Q_{2}=-Q\)を代入できるかがカギになります。

問題[9] 二つの導体の誘導係数の導出　☆☆☆

対策になりそうな大学：九大

電位係数を対策するときは、1問程度解いておくと良いです。

電位係数の方程式とは違い、左辺が電荷\(Q\)になります。

問題[11] 3つの導体球を段階的に接地したときの、各球に残る電荷量　☆☆☆

対策になりそうな大学：全般

接地していく毎に条件が変わることに注意しましょう。\(V_{1}=0⇒V_{2}=0⇒V_{3}=0\)と段階的に置いていきます。

問題[15] 導体球殻の電位係数、容量係数、誘導係数　☆☆★

対策になりそうな大学：全般

これはガウスの法則を利用して解くことができます。

電位係数について詳しく理解していなくても、いつものように計算し、項を比較することで答えを導くことができます。

☆☆☆でも良いかもしれませんが、とっつきやすさから☆☆★とします。

問題[17] 3つの導体間の容量係数、誘導係数　☆☆☆

対策になりそうな大学：東北大

似たような問題が出題されたことがあります。

3つの導体になろうとも方針は変わりません。

その系特有の条件(本問なら\(Q_{1}=Q_{2}=0\)のとき、\(V_{1}=V_{2}=V_{3}\)になることを利用します。

問題[18] 静電遮蔽　☆☆☆

対策になりそうな大学：東北大

少し前ですが、2011年ごろに同じ問題が出題されたことがありました。

教科書によっては説明していることもあります。上記の問題を志望する方は、是非できるようになりましょう。

真空中の導体系

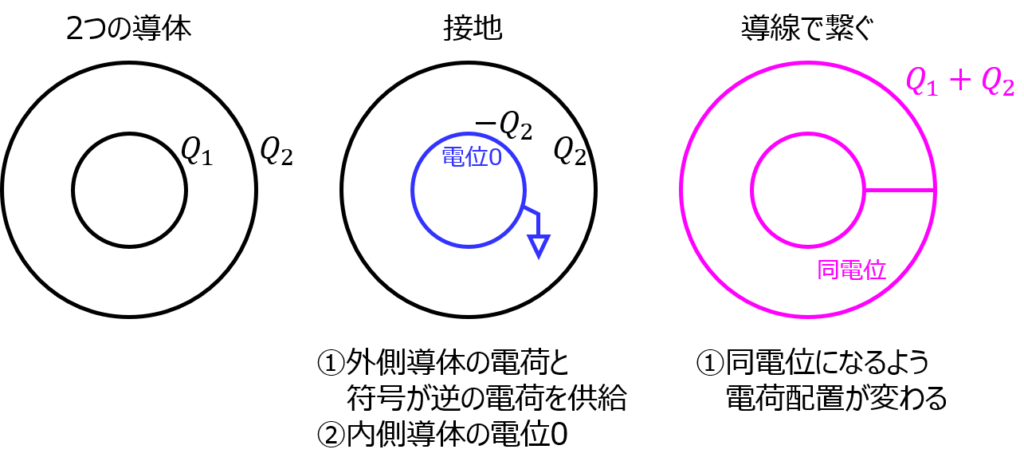
ガウスの法則でただ電場を求めるだけでなく、接地する。導体同士を線でつなぐなど、様々な操作が入ります。

大学受験でも出てきますが、院試でもよく出てきます。

接地する=電位0になるように電荷が誘導される。

など、基本的な原則を確認できます。

問題[23-1] 遠方の導体球に電荷を与えた時の各球の電位　☆★★

対策になりそうな大学：九大

導体間を線でつないで電荷の変化を考える問題は、九大の最新年度の問題で出てきました。

他大学の院試ではなかなか見ず、面食らったかもしれません。

類題演習として確認しておくことをオススメします。

内容自体は高校物理の知識でも解くことができるので☆★★です。

問題[23-2] 遠方の導体球に電荷を与えた時の各球の電位　☆☆★

対策になりそうな大学：九大

問題[23-1]から導体の形状が変わっただけです。理解の確認にどうぞ。

問題[23-4] 3つの導体球を接続した際の電荷量の変化　☆☆☆

対策になりそうな大学：九大

本格的な問題です。[23-3]も同様の問題ですが、導体球を扱う本問の方が院試向きです。

複雑な計算が絡みますが、この問題を解くことができれば一安心でしょう。

問題[24-3] 帯電した導体球を帯電しない導体球に接続したときのエネルギー変化　☆☆★

対策になりそうな大学：全般

導体同士を接続する=同電位になることに気が付いていれば、問題23までの知識で解くことができます。

発想自体は問題[23]までと変わらず、静電エネルギーの公式\(U=\frac{1}{2}CV^{2}\)を知っているかです。

問題[26-1] 直線導体の静電容量　☆☆★

対策になりそうな大学：全般

院試頻出です。必ず確認しましょう。

導体の半径\(a\)は、直線導体間の距離\(2l\)に対し小さいことから、\(a<<2l\)の近似を用いることもあります。

問題[27] 二つの直線導体の静電容量　☆☆★

対策になりそうな大学：全般

26-1と同じく院試頻出です。教科書でも取り上げられることが多いです。

\(d-a<<d\)の近似も良く使います。忘れないようにしましょう。

問題[30] 平行版コンデンサの中に挿入した導体にかかる力　☆☆★

対策になりそうな大学：全般

29-1でも類似の問題が紹介されていますが、個人的には30をオススメします。

理由は、力\(F\)を求めるためにエネルギー\(U\)を位置\(x\)で微分することで求めているからです。

もちろん、高校物理のように\(\delta d\)移動した後のエネルギー変化から考えることもできますが、本記事は院試を想定しています。

複雑な計算をするよりも、微分するだけで求められる前者の方法をオススメします。

問題[34] 球同士を接続したときの電荷の変化　☆☆☆

対策になりそうな大学：九大、阪大

最新の問題で出題がありました。他大学の問題ではあまり見られないですが、九大では対策必須です。

電荷を未知数に置き、電位が同じである条件を用いて方程式を作成。解を求めていきます。

なお、阪大でも類題が一度だけ出たことがあります。(無限遠の導体と接続した場合)

問題[34-2] 様々な接続条件での電荷の変化　☆☆☆

対策になりそうな大学：九大

問題34の類題です。様々な条件で方程式を立てて解いていきます。

問題[37] 絶縁破壊しないための円筒導体の設計　☆☆★

対策になりそうな大学：東大

難しい用語が並んでいますが、要はガウスの法則で求めた電場が閾値を超えないように、あるパラメータを可変にすると解くことができます。

補足

問題40以降はコンデンサ回路が続きます。

大学入試ならば演習する必要がありますが、院試ではあまり出てきません。

本記事では割愛します。

最後に

本章は、院試でよく出題されます。必ず演習しましょう。