下記の開ループ制御系の根軌跡をそれぞれ示せ。ただし、Kはゲインとする。
(1)\(G_{1}(s)H_{1}(s)=\dfrac{K(s+2)}{s(s+1)}\)
(2)\(G_{2}(s)H_{2}(s)=\dfrac{K(s+1)}{s^{2}(s+11)}\)
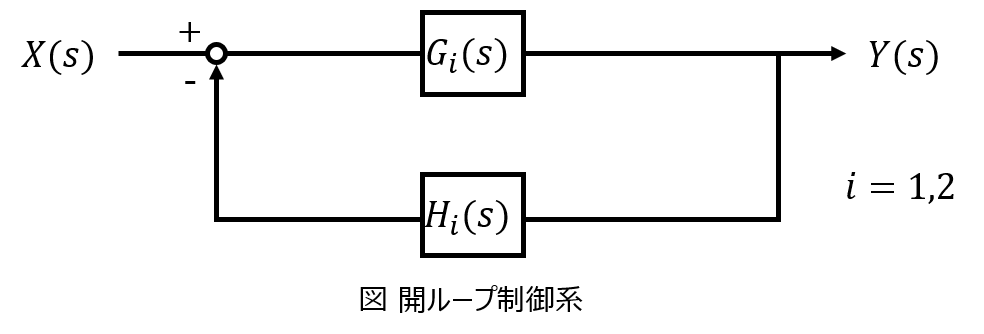
根軌跡とは
ゲインKを0から∞に変化させたときの閉ループ伝達関数の根(極)の軌跡を言います。
以前の記事で、ゲインKを増大させると、システムが不安定になりやすいことを説明しました。
システムが不安定になりやすい=極の実部が正に近づくことを意味しています。
※極の実部が正になると、インパルス応答の\(exp(at)\)項のaが正になり、発散するからです。
では、どのくらいのKでどのくらい実部に近づくのか、制御設計をする上で定量的に知りたくなるはずです。
そこで出てくるのが根軌跡です。
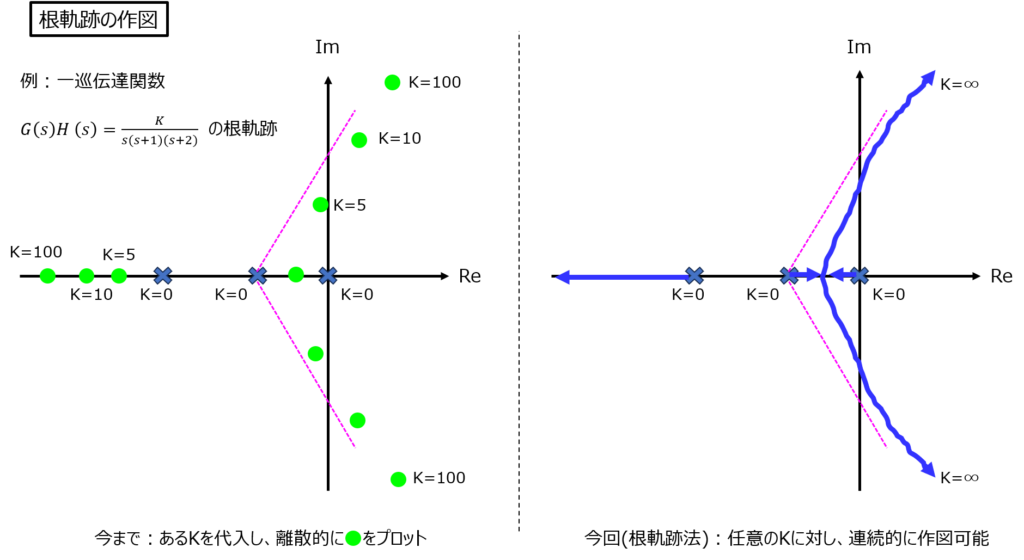
今まで、K=0,1,10,100など、Kの値をそれぞれ代入してその時の極を離散的に求めていました。
根軌跡を作図できるようになると、任意のKに対して連続的に極の軌跡が分かるようになります。
本問では、伝達関数ごとに根軌跡の書き方をパターンで説明していきます。
根軌跡の求め方
下記2つの方法があります。
一巡伝達関数\(G(s)H(s)\)について
- 直接極を計算する方法 (特性方程式 \(1+G(s)H(s)=0\)sの次数が2次以下の時に有効)
- 特性方程式 \(1+G(s)H(s)=0\)を解の公式を用いて解く\(s_{1},s_{2}\)
- 求めた極に虚部が無いとき➡Kをそのまま大きくし、作図する
- 虚部が有るとき➡x=実部、y=虚部と分けてKを消去して方程式を求め、作図する。
- 特性方程式 \(1+G(s)H(s)=0\)を解の公式を用いて解く\(s_{1},s_{2}\)
- 下記1~5を組み合わせて作図する方法 (任意のsの次数に対して使用可能)
- 根軌跡の始点の数は極の個数。終点の数は零点の個数と一致する。
※始点の数に対し終点の数が足りない分は無限遠へ発散する。 - 根軌跡の分岐の数は極の数に等しい
- 根軌跡は実軸に対して上下対称である
- 無限遠店に伸びる根軌跡の漸近線の傾斜角度\(\phi_{k}\)、実軸との交点を\(\sigma_{k}\)とすれば、下記式で与えられる。
- \(\phi_{k}=\dfrac{(2k+1)\pi}{極の次数-零点の次数}\)
- \(\sigma_{k}=\dfrac{極の総和-零点の総和}{極の次数-零点の次数}\)
- 実軸上のある点から右側をみて、\(G(s)H(s)\)の極と零点の数の総和が奇数ならば、その点は根軌跡上にある。
- 根軌跡の始点の数は極の個数。終点の数は零点の個数と一致する。
どちらの方法も、一巡伝達関数に対して評価します。(閉ループ伝達関数ではないので注意してください。)
教科書では、後者の方法ばかり取り上げられていますが、前者の方法もあります。
手計算で極の値をK付きで求めることができれば、後はKを動かすだけで軌跡が描ける。というシンプルな考え方です。
2次式までなら、解の公式を用いて現実的な手計算で求めることができます。
後者の方法を暗記して絶対に根軌跡を作図しなければならない!と思いがちですが、こういった泥臭い方法もあります。場合によって使い分けると良いです。
逆に、分母の次数が3次になると手計算で直接極を求めて軌跡を描くことは難しくなります。
このとき、1~5の手法を用いることで3次以上の式でも概形を書くことができます。
1~5の操作でなぜ軌跡が描けるのか。なる理由(証明)は、難しい数学の知見から出てきているようです。
制御工学は、工学部及び企業の開発で用いられる実学寄りの科目です。
証明問題も、(私が見てきた限りでは)一度も見たことがありませんので、黙って暗記することが吉です。
解答
(1)\(G_{1}(s)H_{1}(s)=\dfrac{K(s+2)}{s(s+1)}\) の根軌跡
こちらは、極を直接手計算で求め、軌跡を描きます。
特性方程式\(1+G_{1}(s)H_{1}(s)=0\)は、下記で与えられる。
\begin{aligned}s^{2}+(1+K)s+2K=0\end{aligned}
極の次数=解の個数である。解の公式を用いて、
\begin{aligned}s&=-\dfrac{1+K}{2}±\dfrac{1}{2}\sqrt{(1+K)^{2}-8K} \\ &= -\dfrac{1+K}{2}±\dfrac{1}{2}\sqrt{K^{2}-6K+1}\end{aligned}
√内の正負を考える。
\(K^{2}-6K+1=0\)を解くと、\(s=3±2\sqrt{2}\)
Kに対して下に凸のグラフであるため、\(3-2\sqrt{2}<K<3+2\sqrt{2}\)の範囲で負の値を取る。
よって、同じ範囲で√の係数は虚数になる。
それ以外のKの範囲では、\(s\)は実数を取る。よって、複素数平面上では実軸を移動する。
以上を整理し、K=0からKを大きくした時の極の動きを考えていく。
なお、2つの極のうち、大きい方を\(s_{1}\)。小さい方を\(s_{2}\)とする。
(i)\(K=0\)のとき
s=0,1で、これを始点とする。
(ii)\(0<K<3-2\sqrt{2}\)のとき
\(s_{1}\)は減少し、\(s_{2}\)は増加する。
\(K→3-2\sqrt{2}\)になったとき、\(s_{1},s_{2}\)は一致する。
(iii)\(3-2\sqrt{2}<K<3+2\sqrt{2}\)のとき
√内は負となり虚数を取るので
\begin{aligned}s= -\dfrac{1+K}{2}±j\dfrac{1}{2}\sqrt{-K^{2}+6K-1}\end{aligned}
\(x=-\dfrac{1+K}{2},y=±\dfrac{1}{2}\sqrt{-K^{2}+6K-1}\)と置き、Kを削除することを考える。
\(K=-(1+2x)\)とし、\(y=±\dfrac{1}{2}\sqrt{-K^{2}+6K-1}\)に代入すると
\begin{gather}y=±\dfrac{1}{2}\sqrt{-(1+2x)^{2}-6(1+2x)-1} \\ y^{2}=\dfrac{1}{4}(-(1+2x)^{2}-6(1+2x)-1) \\ 4y^{2}=-(4x^{2}+16x+8) \\ y^{2}=-x^{2}-4x-2 \\ (x+2)^{2}+y^{2}=2\end{gather}
だから、\((x,y)=(-2,0)\)を中心とした半径\(\sqrt{2}\)の円になる。
(iv)\(3+2\sqrt{2}<K\)のとき
\(s= -\dfrac{1+K}{2}±\dfrac{1}{2}\sqrt{K^{2}-6K+1}\)より、\(s_{2}\)は負の∞へ発散する。零点は\(s=-2\)より、\(s_{1}\)は-2に収束する。
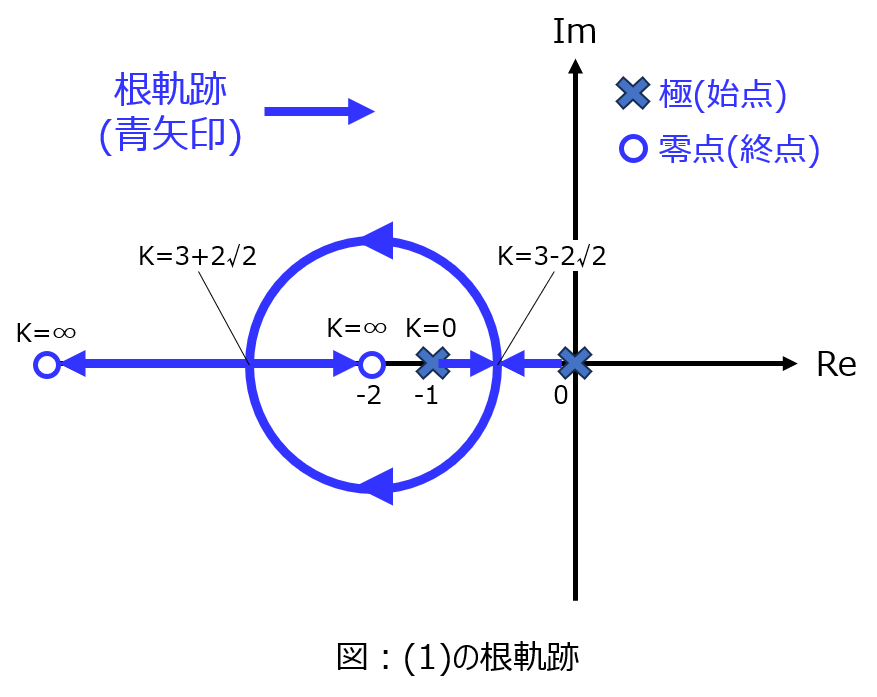
根軌跡の作図
(i)~(iv)から、下記のような根軌跡になる。
(2)\(G_{2}(s)H_{2}(s)=\dfrac{K(s+1)}{s^{2}(s+11)}\)の根軌跡
手順1:始点と終点の数
sの次数について、分母:3次、分子:1次であるため、
始点:s=0(重根),-11 で、 終点 s=-1。始点3つに対して足りない2つの分は、∞へ発散する。
手順2:根軌跡の分岐
分岐の数=極の数なので、3つに分岐する。
手順3:根軌跡は実軸に対して上下対称
この通りです。手順1で、2つの軌跡は∞へ発散することが分かっています。
この段階ではあくまで仮定の域を出ないですが、下記の予想ができます。
ある根軌跡の虚部が正の無限大へ発散するとき、手順3の考え方により虚部が負の無限大へ発散する根も存在する。
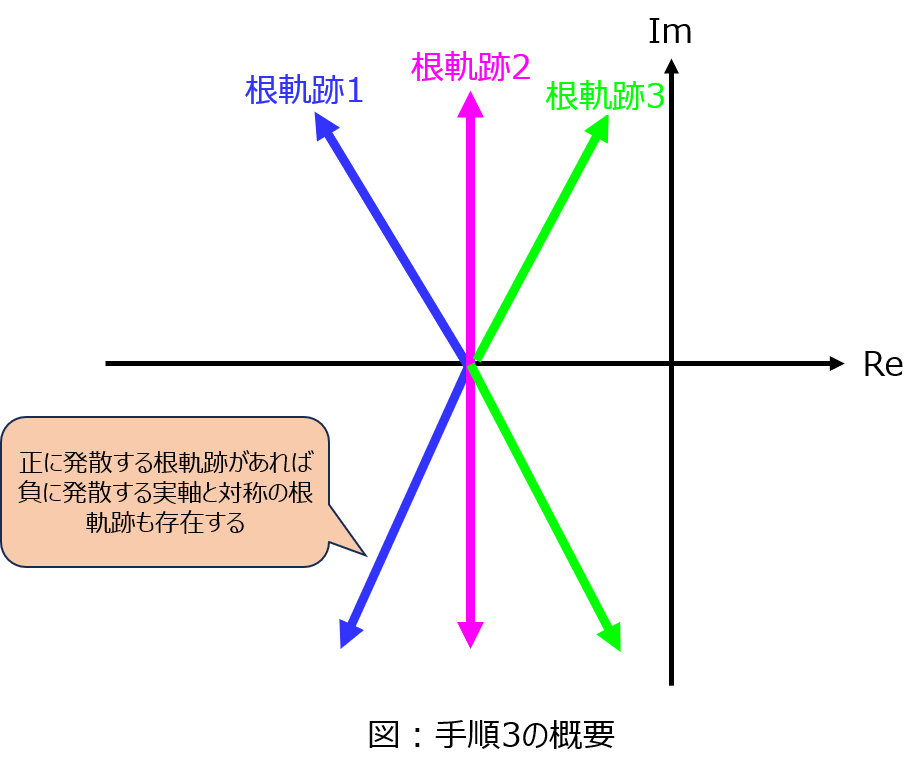
手順4以降で確かめていきましょう。
手順4 漸近線の傾斜角と実軸との交点
傾斜角の算出
漸近線の角度\(\phi_{k}\)は、極の数が3、零点の数が1のため
\begin{aligned}\phi_{k}=\dfrac{(2k+1)\pi}{3-1}\end{aligned}
\(k=-1,0,1\)を代入すると、漸近線の傾斜角は下記になる。
\begin{aligned}\phi=-\dfrac{\pi}{2},\dfrac{\pi}{2},\dfrac{3}{2}\pi\end{aligned}
実軸の交点
極の総和は N=0+0-11=-11、零点の総和はM=-1
\begin{aligned}\sigma=\dfrac{-11-(-1)}{3-1}=-5\end{aligned}
手順5 実軸上の点から右を見た時、零点と極の数の和が奇数なら、その点は根軌跡上にある
例えば、s=-3を考えます。
零点は、s=-1なので1つ、極はs=0(重根)なので2つ。合計3つ。
奇数なので、s=-3は根軌跡上にあることが分かります。
s=-11が始点なので、s=-3に向かっていることが分かります。
s=-1まで零点と極の和が奇数のため、s=-11を始点とする根軌跡は、終点s=-1まで実軸を通って移動することが分かります。
また、s=0(重根)を始点とする根軌跡は、手順4で求めた漸近線を元に無限大へ発散することが分かります。
根軌跡の作図
手順1~5より、下記の図が描けます。
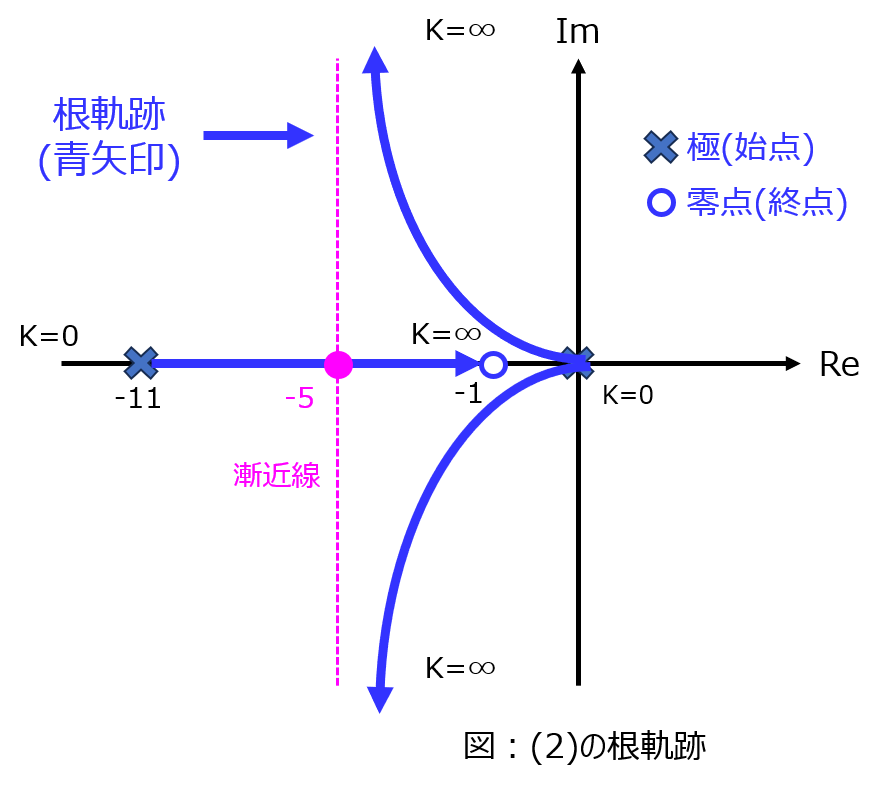
最後に
根軌跡は、東大、阪大の院試にてよく出題されます。
古典制御の一番最後の単元のため、対策が間に合わない傾向にありますが、その穴をつくように出題されます。
また、電験の二次試験でも出題されることがあります。
安定判別をする上でも有用なので、是非知っておきたい知識です。