【水力発電】ベルヌーイの定理の導出と使用方法の説明

【問題】

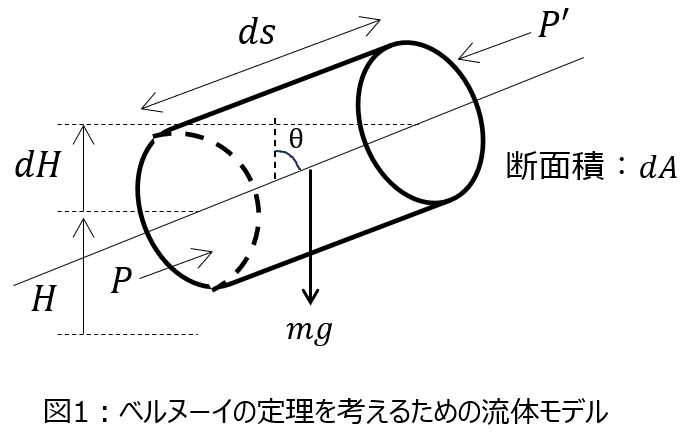
図1は、水力発電に必要なベルヌーイ(Bernoulli)の定理を導出するためのモデルを示している。水の流線に沿って座標軸$s$を取り、座標sの位置に底面積$dA$、高さ$ds$の水の微小円柱を考える。流れの上流面、下流面にかかる圧力をそれぞれ$P$、$P^{\prime }$とする。図のように、円柱の軸は鉛直方向と角度$\theta$をなし、上流面、下流面のそれぞれ中心の高さは$H$、$H+dH$である。重力加速度を$g$、水の質量密度を$\rho$として、下記の導出過程の(i)～(v)にそれぞれ適した式を答えなさい。

• 円柱の質量を$m$として、円柱にかかる重力軸向きの成分を$\theta$として表すと(i)となるが、$m$、$\theta$を用いず、$dA,ds,dH$で表すと、(ii)になる。
• 円柱にかかる座標軸方向の圧力は$PdA-P^{\prime }dA$で、$P^{\prime }=P+{\displaystyle \frac{dP}{ds}}ds$とすると、(iii)と整理される。
• 円柱の座標軸方向の速度を$v$とし、加速度を$v{\displaystyle \frac{dv}{ds}}$とすると、運動方程式は(iv)となる。共通の係数を消去して、全ての項を左辺に移して(v)となる。
• (v)をsで積分して、ベルヌーイの定理$$\begin{array}{}\text{(1)}& \begin{array}{r}\rho gH+{\displaystyle \frac{1}{2}}\rho v^2+P=const\end{array}\end{array}$$を得る。

神戸大学 電気電子工学専攻 電力工学 2022より抜粋

ベルヌーイの定理とは

流体が地点Aから地点Bに流れるときの関係を表した式です。

$$\begin{array}{}\text{(2)}& \begin{array}{r}\rho g{H}_A+{\displaystyle \frac{1}{2}}\rho v_A^2+P_A=\rho g{H}_B+{\displaystyle \frac{1}{2}}\rho v_B^2+P_B\end{array}\end{array}$$

それぞれの項は、下記の単位体積当たりのエネルギーを示しています。

1,2項は高校物理(力学)で勉強した通りです。3項は覚えた方が良いです。(熱力学で同様の法則があるかもしれませんが)

ある地点AがBより高いとすると、地点Bで発生する速度は地点Aより大きいと考えられます。よって、運動エネルギーもAより大きいはずですが、その分位置エネルギーが小さくなります。

このようなイメージで、等号=が成立するわけですね。

なお、この想定は流路に圧力損失が無い想定です。(理想流体)

ベルヌーイの法則の導出 (解答例)

(i)(ii)円柱の表示方法

(i)円柱にかかる重力は$mg$で、$\theta$でベクトル分解すると、座標軸$s$上の成分は

$$\begin{array}{}\text{(3)}& \begin{array}{r}\mathbf{|}\mathit{d}\mathit{s}|=mg\cos \theta \end{array}\end{array}$$

(ii)質量$m$について、密度*体積の関係から

$$\begin{array}{}\text{(4)}& \begin{array}{r}m=\rho dAds\end{array}\end{array}$$

$\cos \theta ={\displaystyle \frac{dH}{ds}}$より

$$\begin{array}{}\text{(5)}& \begin{array}{r}\rho dAdsg{\displaystyle \frac{dH}{ds}}\end{array}\end{array}$$

(iii)円柱にかかる座標軸方向の圧力

(iii)円柱にかかる合計の力$F$は

$$\begin{array}{}\text{(6)}& \begin{array}{r}F=PdA-P^{\prime }dA-\rho gdAdS\cos \theta \end{array}\end{array}$$

地点間の圧力差$dP$は、$dP=P^{\prime }-P\iff (P-P^{\prime })dA=-dPdA$より

$$\begin{array}{}\text{(7)}& \begin{array}{r}F=-dPdA-\rho gdAds\cos \theta \end{array}\end{array}$$

(iv)円柱の運動方程式

$F=m{\displaystyle \frac{dv}{ds}}$を、(iii)の結果に代入し

$$\begin{array}{}\text{(8)}& \begin{array}{r}m{\displaystyle \frac{dv}{ds}}=-dPdA-\rho gdAds\cos \theta \end{array}\end{array}$$

これに、(ii)の結果を代入し

$$\begin{array}{}\text{(9)}& \begin{array}{r}\rho dAdsv{\displaystyle \frac{dv}{ds}}=-dPdA-\rho gdAds{\displaystyle \frac{dH}{ds}}\\ \rho v{\displaystyle \frac{dv}{ds}}+{\displaystyle \frac{dP}{ds}}+\rho g{\displaystyle \frac{dH}{ds}}=0\end{array}\end{array}$$

(v)ベルヌーイの法則の導出

(iv)の結果から$ds$を削除し、各項の微小パラメータで積分することで

問題文で与えられたベルヌーイの定理

$$\begin{array}{}\text{(10)}& \begin{array}{r}\rho gH+{\displaystyle \frac{1}{2}}\rho v^2+P=const\end{array}\end{array}$$

を得る。

ベルヌーイの法則の使い方の一例

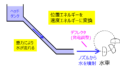
以前の記事で、吸出し菅を使用したときにキャビテーションが発生するとお話ししました。

これを、ベルヌーイの法則を用いて説明してみます。

吸出し高さを$H_1$、ランナ出口の圧力を$P_1$、流速を$v_1$
吸出し菅の出口深さを$H_2$、圧力を$P_2$、流速を$v_2$、吸出菅内の損失水頭を$H_d$とすればベルヌーイの定理より

$$\begin{array}{}\text{(11)}& \begin{array}{r}{H}_1+H_2+{\displaystyle \frac{P_1}{\rho g}}+{\displaystyle \frac{v_1^2}{2g}}={\displaystyle \frac{P_2}{\rho g}}+{\displaystyle \frac{v_2^2}{2g}}+H_g\end{array}\end{array}$$

大気圧を$P_a$とすれば、

$$\begin{array}{}\text{(12)}& \begin{array}{r}{\displaystyle \frac{P_2}{\rho g}}=H_2+{\displaystyle \frac{P_a}{\rho g}}\end{array}\end{array}$$

だから、

$$\begin{array}{}\text{(13)}& \begin{array}{r}{\displaystyle \frac{P_1}{\rho g}}={\displaystyle \frac{P_a}{\rho g}}-H_1-({\displaystyle \frac{v_1^2}{2g}}-{\displaystyle \frac{v_2^2}{2g}}-H_d)\end{array}\end{array}$$

吸出し菅の形状より、出口の断面積が大きいため、$v_2$は小さくなる。

このとき、左辺の$P_2$も小さくなる。

よって、回復水頭が発生するが、キャビテーションのリスクが高まる。

参考文献

電力発生工学：加藤政一・中野茂・西江嘉晁・桑江良明(共著)、第2章