以下は、原子力発電で利用または将来利用が期待される核分裂および核融合の反応式である。
\begin{cases}\ce{^{35}U}+\ce{^{1}n}→\ce{^{95}Y}+\ce{^{139}I}+N_{1}\ce{^{1}n} \\ \ce{^{35}U}+\ce{^{1}n}→\ce{^{96}Rb}+\ce{^{137}Cs}+N_{2}\ce{^{1}n} \\ \ce{^{2}D}+\ce{^{3}T}→\ce{^{4}He}+\ce{^{1}n} \\ \ce{^{2}D}+\ce{^{2}D} → (A)+\ce{^{1}p} \end{cases}
ここに、\(n\)は中性子、\(p\)は陽子、\(D\)は重水素、\(T\)は三重水素で、左肩の数字は質量数を示す。以下の問いに答えなさい。
(a)U(ウラン)、Y(イットリウム)、Rb(ルジビウム)の原子番号は、それぞれ92,39,37である。I(ヨウ素)及びCs(セシウム)の原子番号はいくらか。
神戸大学大学院 電気電子工学専攻 2022 より引用
(b)(1)および(2)の反応で発生するn(中性子)の個数、それぞれ\(N_{1},N_{2}\)を答えなさい。
(c)p(陽子)以外の(4)の反応の生成物(A)を答えなさい。
(d)(3)の反応で発生するエネルギーを17.5MeVとして、Heおよびnにそれぞれ分配されるエネルギーを求めなさい。但し、両者の質量は質量数に比例し、反応前にエネルギーは発生するエネルギーに対して無視できるとする。
はじめに
過去の記事で、原子力発電の発電原理について述べました。
核分裂、核融合反応時、エネルギーが放出されるので、この時に水を蒸気にして発電します。
本記事では、化学反応式に基づいて核分裂、核融合の様子を見ていきます。
化学反応式の見方
- 左辺と右辺の中性子、陽子の個数は一致する
- 質量数=中性子数+陽子数
- 原子番号=陽子の数
高校化学の知識に忠実に従うことで解くことができます。
もちろん、最低限の原子番号の暗記は必要ですが、原子番号が分かれば陽子が分かり、中性子も分かる流れになります。
核分裂により分配されるエネルギー
質量比に依存します。
分裂後に発生する物質1の質量を\(M_{1}\)、物質2の質量を\(M_{2}\)とし、核分裂により発生するエネルギーを\(E\)とします。質量1の持つエネルギーを\(E_{1}\)、質量2の持つエネルギーを\(E_{2}\)とすると、下記の関係式になります。
\begin{cases}E_{1}=\dfrac{M_{2}}{M_{1}+M_{2}} \\ E_{2}=\dfrac{M_{1}}{M_{1}+M_{2}}\end{cases}
これは、衝突の関係式を考えるとイメージしやすいです。
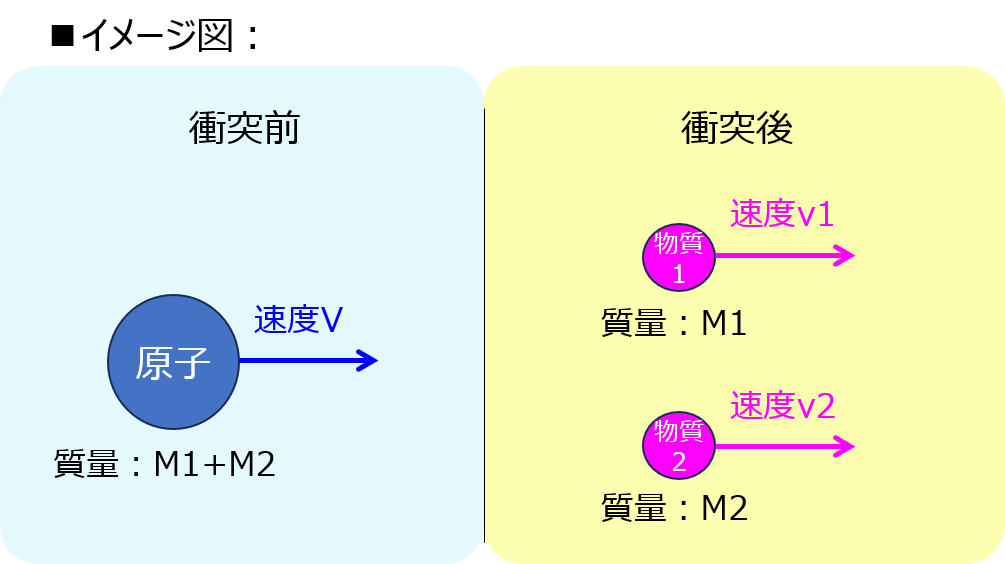
衝突前の速度を\(V\)、衝突後の物質1、物質2の速度をそれぞれ\(v_{1},v_{2}\)とすると
\begin{aligned}(M_{1}+M_{2})V=M_{1}v_{1}+M_{2}v_{2}\end{aligned}
が成立すると仮定します。エネルギーを最小にする観点で速度を分配するとすると、\(M_{1}v_{1}=M_{2}v_{2}\)のため
\begin{aligned}v_{1}:v_{2}=\dfrac{M_{2}}{M_{1}+M_{2}}:\dfrac{M_{1}}{M_{1}+M_{2}}\end{aligned}
の比が成立します。この考え方を式(3)に適用しているわけですね。
解答例
(a)ヨウ素とセシウムの原子番号
原子番号表を暗記していれば即答できるかもしれませんが、誘導に従います。
(1)式のうち、第一式に注目する。左辺のウラン、右辺のイットリウムの原子番号92,39の差を取ると、ヨウ素の原子番号(92-39=53)を求められる。
次に、セシウムの原子番号について、第二式に注目する。今度はウランの原子番号に対し、ルビジウムの原子番号の差を取れば良いので、92-37=55
(b)中性子の個数
原則1,2を利用する。
まず、第一式の左辺で発生する中性子の個数を考える。
ウラン:235-92=143個で、第2項の中性子1個分を合わせ、合計144個存在する。
右辺について、イットリウム:95-39=56個で、ヨウ素:139-53=86。合計56+86=142個存在する。
\(N_{1}\)は左辺と右辺の差分存在するので、\(N_{1}=144-142=2\)
次に、\(N_{2}\)について、第二式について同様にして
左辺:第一式と同じなので144個
右辺:ルビジウム:96-37=59、セシウム:137-55=82。合計:59+82=141個
以上より、\(N_{2}=144-141=3\)
(c) 陽子以外の生成物(A)
(b)と同じく、左辺、右辺の中性子数、陽子数を考える。
| 辺 | 中性子数 | 陽子数 | |
| 重水素\(D\) | 左辺 | 1 | 1 |
| 三重水素\(T\) | 左辺 | 2 | 1 |
| (A) | 右辺 | 2 | 2 |
| 陽子\(p\) | 右辺 | 1 | 0 |
(A)は中性子数2、陽子数2であることが分かります。
原子番号=陽子数なので、原子番号2のヘリウムであることが分かります。
質量数は中性子数と陽子数の和のため、4です。
(d) 分配されるエネルギー
式(2)より、He、nに分配されるエネルギー\(E_{1},E_{2}\)は
\begin{cases}E_{1}=\dfrac{1}{4+1}*17.5=3.5[MeV] \\ E_{2}=\dfrac{4}{4+1}*17.5=14.0[MeV]\end{cases}