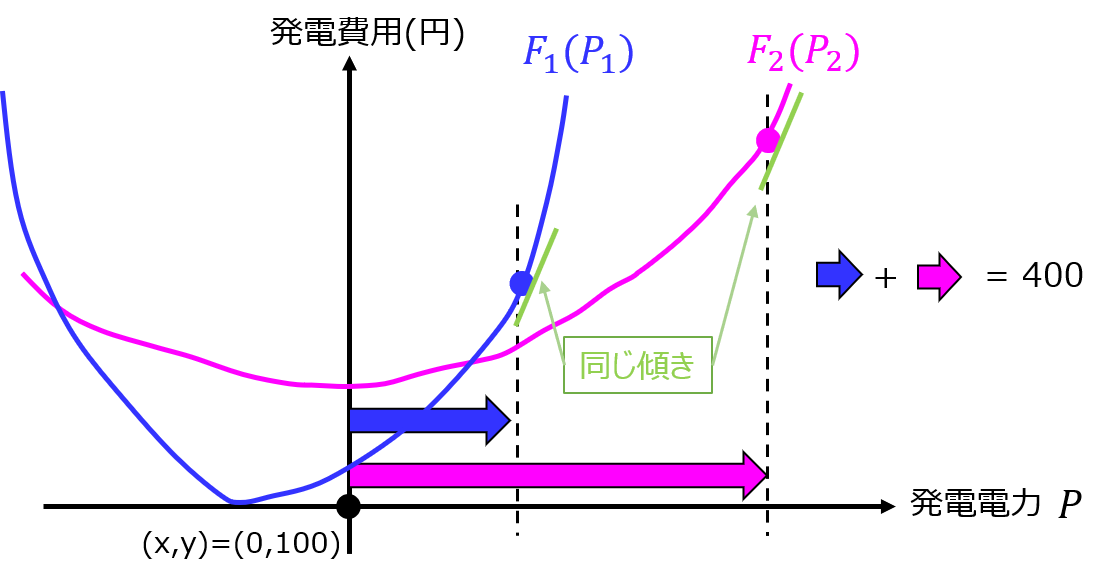
【問題】ある電力系統に火力発電所が2基連携している。それぞれの発電電力[MW]を\(P_{1}、P_{2}\)、発電費用[円]を\(F_{1}(P_{1})、F_{2}(P_{2})\)とし、それぞれ下記で表すことができるとする。
\begin{eqnarray}F_{1}(P_{1})=100+8P_{1}+6P_{1}^{2} \\ F_{2}(P_{2})=200+4P_{2}+2P_{2}^{2}\end{eqnarray}
負荷で消費する電力が400[MW]であり、\(P_{1}+P_{2}=400\)が常に成立するとき、合計の発電費用が最小となる\(P_{1}、P_{2}\)を求めよ。
はじめに
電力関係の問題の解説は、先駆者様のサイトが多々あります。本分野において、新規性のある記事がどこまで書けるか未知ですが、第1回目は等増分燃料費の法則について扱います。
作成した理由は下記です。
- 等増分燃料費の法則の式の結果のみを使用して解説していることが多いから
- 背景、イメージ論からの説明が少ないと感じたから
確かに、工学系の技術者としては結果だけ知っていれば与えられた問題に対して答えを出すことはできます。しかし、それが正しいことを他者に説明するうえでイメージ、理由について語ることはほぼ必須です。
こういった時に躓かないように、数学的な素養を身に着ける材料の一つになれば良いなと考え解説することにしました。
本記事は4章に分かれていますが、2章目の解説がネットに少ないと感じます。是非そこだけでも参考に下さると幸いです。
等増分燃料費の法則とは
\begin{aligned}\dfrac{\partial F_{1}}{\partial P _{1}}=\dfrac{\partial F_{2}}{\partial P_{2}}=\ldots =\dfrac{\partial F_{i}}{\partial P_{i}}\end{aligned}
の関係式になります。
それぞれの発電機のある負荷点における発電費用の微分係数が全て一致するとき、制約条件下で燃料費が最小になる。ことを示しています。
ラグランジュの未定乗数法という数学的法則から立式できます。(下記)
ラグランジュの未定乗数法
\(P_{1}~P_{i}\)を変数に持つ関数\(L(P_{1},P_{2},・・・P_{i},\lambda)\)が制約条件\(g=0\)の下で極値を取るとき、その極値を与える\(P_{1},P_{2}・・・P_{i}\)は以下の条件で求められる。
\begin{aligned}\dfrac{\partial }{\partial P_{1}}\left( L-\lambda g\right) =\dfrac{\partial }{\partial P_{2}}\left( L-\lambda g\right) =\dfrac{\partial }{\partial P_{i}}\left( L-\lambda g\right) =0\end{aligned}
これだけ見るとよく分からないと思います。本問を例に説明していきます。
ラグランジュの未定乗数法を用いて例題を解いてみる
本問の目的は、総発電費用\(L=F_{1}(P_{1})+F_{2}(P_{2})\)を制約条件\(g=P_{1}+P_{2}=400\)の下で最小化することです。
これにより、偏微分対象のラグランジュ関数\(L- \lambda g\)は下記で与えられます。
\begin{eqnarray}L- \lambda g=300+8P_{1}+6P_{1}^{2}+4P_{2}+2P_{2}^{2}-\lambda(P_{1}+P_{2}-300)\end{eqnarray}
これを各変数\(P_{1}、P_{2}、\lambda\)で偏微分すると以下になります。
\begin{eqnarray}8+12P_{1}-\lambda=0 \\ 4+4P_{2}-\lambda=0 \\ P_{1}+P_{2}-400=0\end{eqnarray}
(6),(7)式目を使用し\(\lambda\)を削除すると、\(P_{1}\)と\(P_{2}\)の関係式を求められます。
その結果を(8)式に代入すると、答えが出そうです。
しかし、これらの式はどこかで見たことがありませんか?
ラグランジュの未定乗数法で立式した式の意味
まず、(6),(7)式ですが、等増分燃料費の法則を表します。
前章の説明の通り、\(\lambda\)を削除すると、以下の関係式が生まれます。
\begin{aligned} 8 + 12 P_{1} = 4 + 4P_{2} = \dfrac{\partial F_{1}}{\partial P _{1}} = \dfrac{\partial F_{2}}{\partial P_{2}} \end{aligned}
前節では、制約条件を加味したラグランジュ関数\(L-\lambda g\)を作成しました。しかし極値を与える変数を求める際に、結局\(\lambda\)は消えます。
この結果から、極値を与える変数を求めるだけならば、ラグランジュ関数を作成せずとも各\(F_{i}(P_{i})\)を\(P_{i}\)で偏微分して=で結ぶだけで良いことが分かります。
これが、等増分燃料費の法則導出の背景です。
(8)式は、問題文中に与えられた制約条件で最初から分かっています。未定乗数法を使わずとも分かる式です。
解答例とそのイメージ
大体答えは出たようなものですが、最後の値まで算出します。
解答例
(8)式を整理して、\begin{eqnarray}12P_{1}-4P_{2}=-4 \\ P_{2}=3P_{1}+1\end{eqnarray}
これを制約条件\(P_{1}+P_{2}=400\)に代入して
\begin{eqnarray}4P_{1}=399 \\ P_{1}=99.75\end{eqnarray}
これより、\(P_{2}=300.25\)であることが分かりました。
イメージ
「等増分燃料費の法則」の名前から察する方もいらっしゃるかもしれません。
解答例で求めた\(P_{1}、P_{2}\)は、その点における\(F_{1}(P_{1})\)と\(F_{2}(P_{2})\)の傾きが等しいことを意味しています。
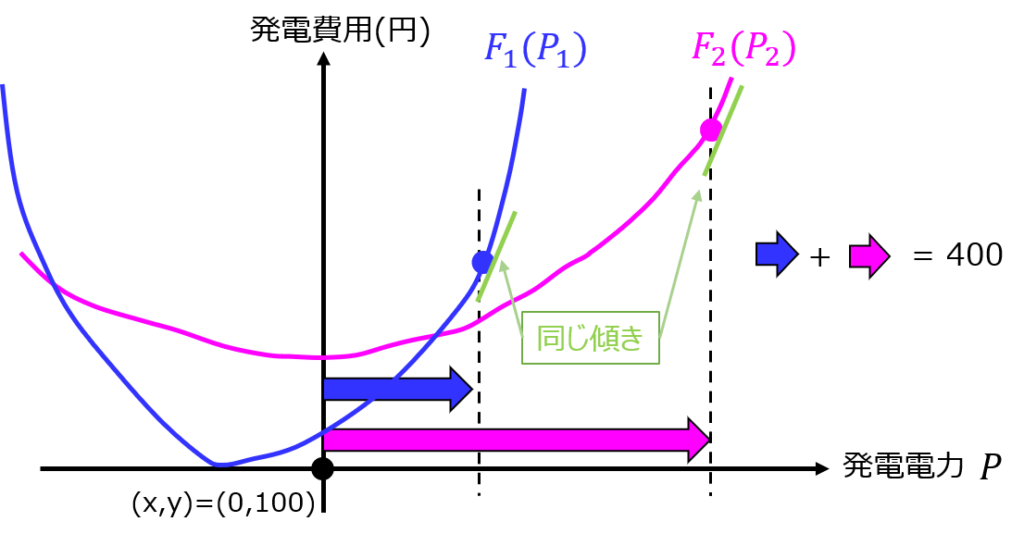
\(P_{1}、P_{2}\)をさらに発電費用を最小化できる点が無いか点を動かすが、発電機1の発電費用の増加/減少分に対し、発電機2の費用の減少/増加分が不足する。
➡合計発電費用は高くなってしまうことが分かります。
これにより、極値を与える点が発電費用として最小であることが分かります。
補足
ラグランジュの未定乗数法は最小値を求めるものではない
ラグランジュの未定乗数法は、ある制約条件下で「極値」を与える変数を算出することができる方法です。
今回、例題で与えた関数は下に凸だったため、極小値しかありませんでした。ですので、最小値が求まります。
逆に、上に凸のグラフが与えられたときは、極大値が求まり、最大値が求められます。
得られたパラメータは現実的に取りうる値とは限らない
例えば、負荷で電力消費が無い状態\(P_{1}+P_{2}=0\)を考えます。
このとき、発電費用を最小にする\(P_{1},P_{2}\)は、\(P_{1}=P_{2}=0\)より300円と計算できます。
しかし、ラグランジュの未定乗数法で計算してみるとどうなるのでしょうか。
(10)式より、\(4P_{1}=-1 ⇔ P_{1}=-0.25\)と負の値になります。問で考える対象は発電機のため、負に発電することは一般的に考えていないです。
このように、変数が取りうる値の範囲外で極値を求める可能性もあります。
また、元も子も無いですが、発電しないならば、そもそも発電機を停止するという考え方もあります。
\(F{P_{1},F{P_{2}\)の定数項\((100,200)\)は、発電機を駆動させるための補機電力を指しています。発電機を停止するならば、補機を動かす必要もなくなり、\(F{P_{1},F{P_{2}=0)\になる算段です。
(ただ、再始動には大きな電源を必要とします。発電しないからと言って補機を停止することが最適解とは限りません。)
最後に
本問では、ラグランジュの未定乗数法を用いた最適発電負荷配分と留意事項を述べました。
資格試験で出題される可能性は低いですが、電気設備設計の実業務を行う際に使用するかもしれません。