水力発電に関する以下の問いに答えよ。
(a)流量\(20.0m^{3}/s\)、有効落差\(81.0m\)の水源から得られる発電電力を求めなさい。ただし、水の比重は1.00、重力加速度は\(9.80m/s^{2}\)、水車及び発電機の効率をいずれも100%とする。
水力発電で用いる水車は、その形式毎に適した回転数があり、相似形の水車の比速度で表される。有効落差\(H\)で使用される回転数\(N\)、出力Pの水車の比速度\(N_{s}\)は、\begin{aligned}N_{s}=N\frac{P^{1}{2}}{H^{5}{4}}\end{aligned}で与えられる。
(b)ある水車を(a)の水源で使用する場合、\(N_{s}≦228rpm\)の制限がある。この\(N_{s}\)は(m-kW)で定義される値である。この水車の実際の回転数の上限を求めなさい。ただし、水車の出力は(a)で求めた発電電力に等しいと考えなさい。
神戸大学 電気電子工学専攻 院試 電力工学 2023より
水力発電とは
水の持つ力学的エネルギーを電気エネルギーに変換することを言います。
ニュースでも良く目にする用語で、イメージはできるかもしれません。理科的な文言で説明すると上記になります。
下記の流れでエネルギー変換。発電します。
- 流れた水でプロペラを回し、回転エネルギーを得る。
- 回転エネルギーを電磁誘導の法則を用いて、磁気エネルギー➡電気エネルギーに変換する。
火力発電、原子力発電も同じ考え方です。
水力発電のように、水(液体)では無いですが、水蒸気でプロペラ(タービン)を回します。
水車の種類
大きく分けて2種類あります。
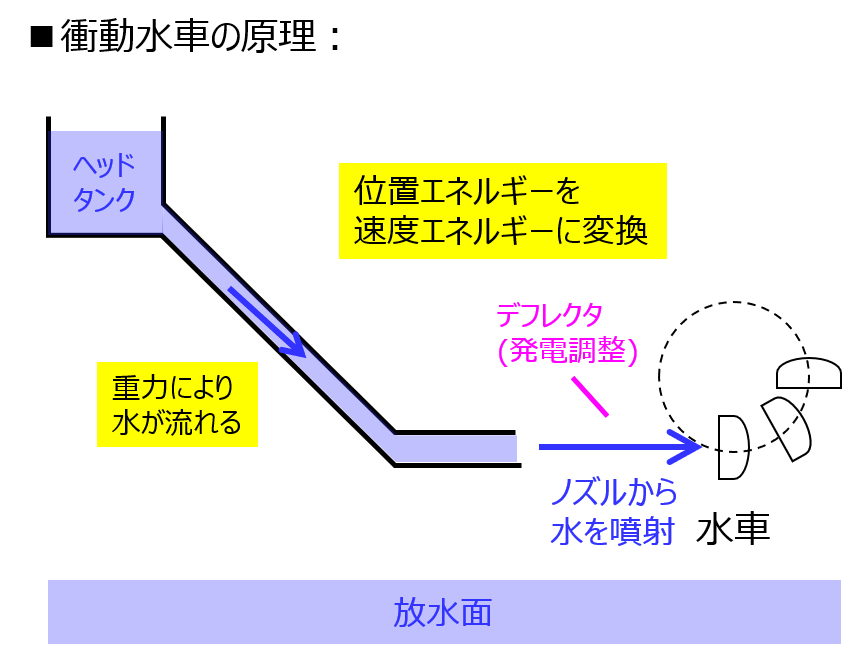
衝動水車
上流から流れてきた水を速度エネルギーに変換し、ノズルから水車のランナ(バケット:水の受け口)に水をぶつけて回転させるものです。
有効落差の高い発電所でよく使います。
衝動水車の種類としては、ペルトン水車があります。
出力調整には、デフレクタを用い、ランナに当たる水量を調節します。
反動水車
衝動水車のように、水を直接ぶつけて回転させるのではなく、水が流れた時に発生する反作用で回転します。
縦軸フランシス水車の場合を下記に示します。水車がある高さまで水が落ちた時、円環上の流路に沿って水が流れ、径方向に設置されているガイドに周方向の力がかかります。
この結果、周方向に回転し発電する。という流れになります。
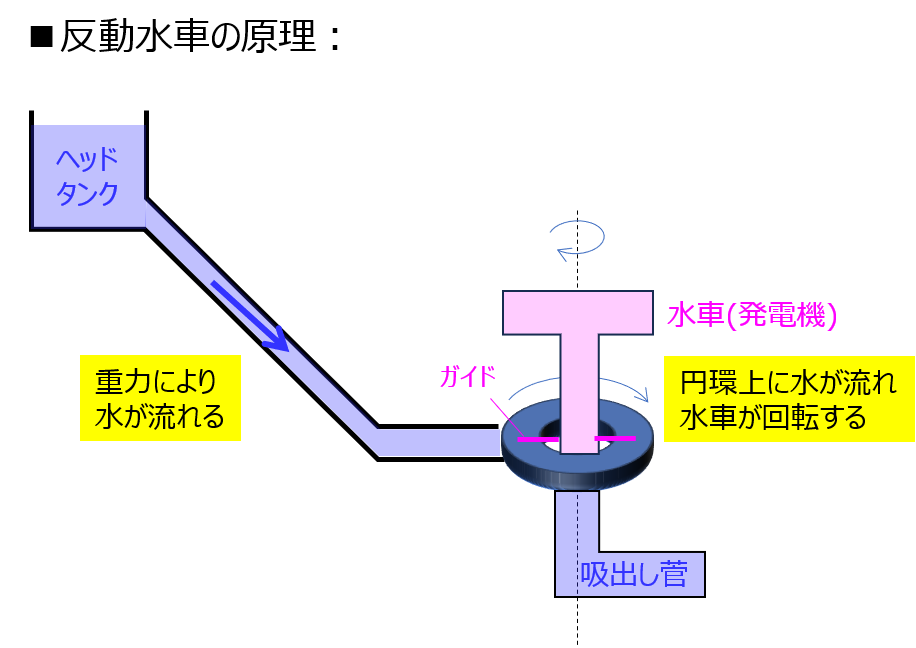
なお、発電機を地面に設置することはできないので、どうしても設置した高さ分有効落差が小さくなります。物理的に、どうしても発電電力が低下します。
吸出管を使用すると、この問題を低減することができます。
吸出菅は、ランナの出口から放水路に向かって、出口の断面積が大きくなっている頂点が無い円錐状の管です。
出口の断面積が大きくなるので、単位時間当たりの速度が小さくなります。これにより、ランナの出口での圧力も小さくなります。有効落差が小さくなり、発生した損失のいくつかを出力に戻すことができます。(回復水頭と言います。)
吸出菅を利用することのデメリット
ランナ出口の圧力が小さくなり、飽和水蒸気圧を下回ると気泡が発生します。気泡が破裂すると、ランナにダメージが入り、穴が開きます。
これをキャビテーションと言います。
キャビテーションを防止するためには、以下の方策があります。
- 吸出し菅の高さを低くする。
- 吸出し菅内に空気を送り込み、圧力を高くする。
補足
他、カプラン水車を初め、様々な水車がありますが、本記事では取り上げないことにします。
まずは、発電電力の計算や、上記で説明した概要の理解を急ぐ方が、試験での得点期待値が上がります。
本記事の最後に参考文献を紹介します。そこで、落差毎によく使われる水車の種類の理解を進めると良いです。
発電電力の計算
まず、下記の式を覚えましょう。
\(P:発電電力、\rho:水の密度、h:有効落差、Q:流量、\eta_{1}:水車の効率、\eta_{2}:発電機の効率\)とし
\begin{aligned}P=\rho g h Q \eta_{1} \eta_{2}\end{aligned}
で表されます。
イメージとしては、高校物理で勉強した位置エネルギー\(mgh\)を流体に対して適用します。
\(g,h\)は共通で、\(m=\rho Q\)とすると、(1)式になります。
流量が多いほど、単位時間当たりの通過体積が大きくなるので、\(m\)が大きくなる理屈ですね。
比速度とは
考えている水車と相似な水車を仮想し、1mの落差で1kWの出力を発生させるときの回転速度を言います。
(1)式で表すことができます。
要は、水車の発電電力が大きく、有効落差が低いほど、回転速度が高い=比速度が大きい となります。
出力\(P\)を一定に取り、回転速度\(N\)を大きくとるほど、発電機をコンパクトにすることができ、経済的です。
ただし、水の圧力水頭が小さくなるため、キャビテーションが発生するリスクが高まります。
解答例
(1) 発電電力の算出
(2)式より
\begin{aligned}P&=9.8*81*20*1*1 \\ &=15876[kW] \\ &=15.9[MW]\end{aligned}
(2) 回転数の上限
(1)式に各パラメータを代入する。
まず、\(P^{\frac{1}{2}}=\sqrt{15876}=126\)
\(H^{\frac{5}{4}}=81.0^{\frac{5}{4}}=243\)より
\begin{aligned}N&≦228*\dfrac{243}{126} \\ &≦439.7\end{aligned}
以上より、回転数の上限は、439.7rpm
参考文献
電力発生工学:加藤政一・中野茂・西江嘉晁・桑江良明(共著)、第2章