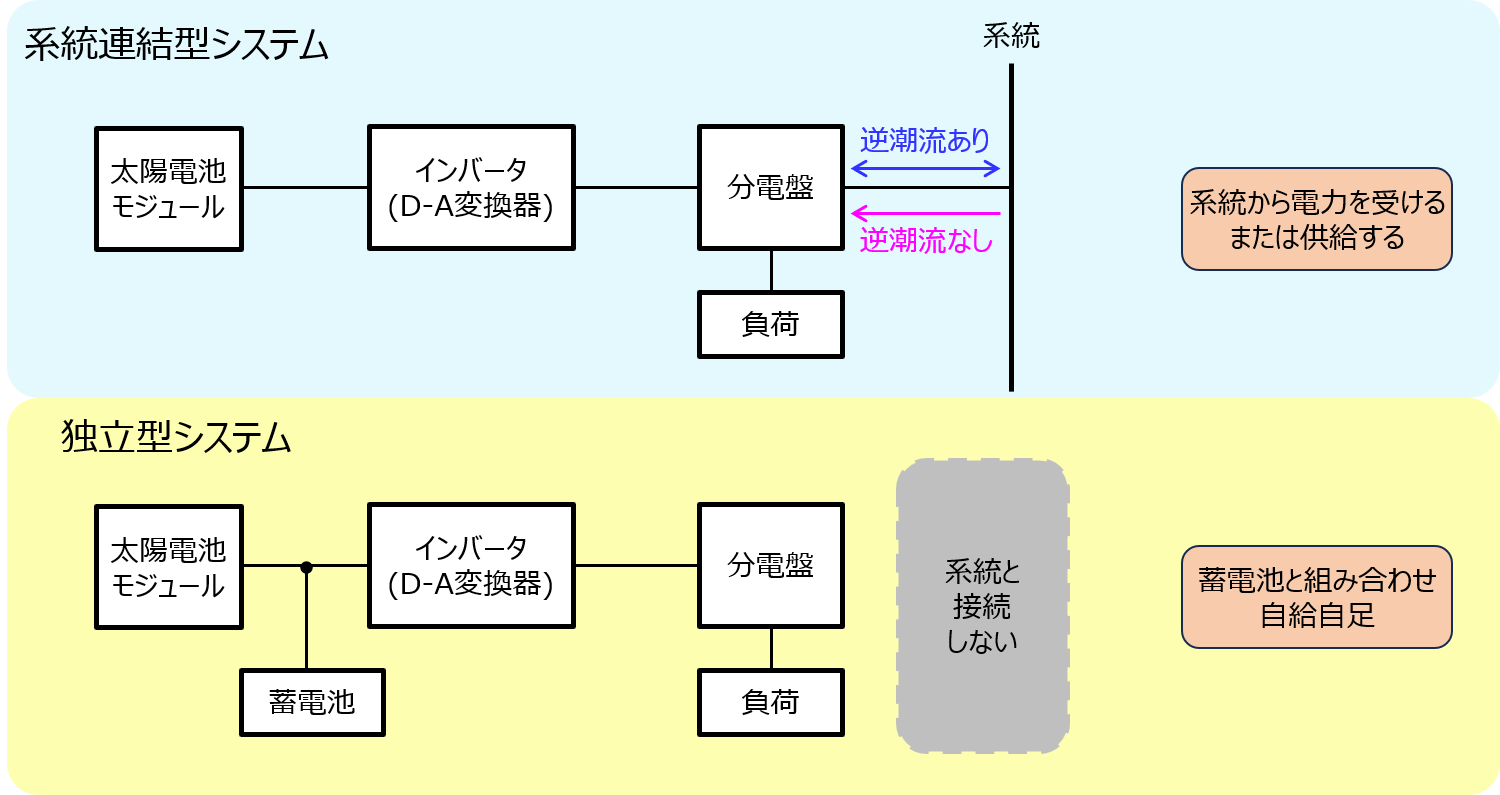
典型的な太陽電池の電流(I)-電圧(V)特性は、光の照射下では\begin{aligned}I=I_{S}-I_{0}\left(e^{\frac{qV}{k_{B}T}}-1\right)\end{aligned}と表される。ここに、\(I_{S},I_{0}\)はそれぞれ短絡電流、逆方向飽和電流、\(q,k_{B},T\)はそれぞれ電気素量、ボルツマン定数、温度である。以下の問いに答えなさい。
(a)縦軸を電流(I)、横軸を電圧(V)として、電流-電圧特性のグラフの概形を描きなさい。短絡電流\(I_{S}\)と開放電圧\(V_{oc}\)はグラフ中に明示しなさい。
(b)縦軸を電力(P)、横軸を電圧(V)として、(a)と同じ太陽電池の電力-電圧特性について、グラフの概形を描きなさい。軸は(a)のグラフと共用して重ね書きし、(a)と区別するために、破線で描きなさい。
(c)太陽電池を最大効率で使用する電圧の条件を、(b)の解答を引用して答えなさい。
神戸大学 電気電子工学専攻 電力工学 2023 問題Dより抜粋
太陽電池とは
光電効果を用いて、受光した光を電流に変換。発電する素子を言います。
最近流行りの太陽光発電が最たる例です。
機械的動作をせず、排ガスを出しません。この観点から、環境適合性が高いです。(クリーンエネルギーと言われています。)
一方で、日光が当たる時間とそうでない時間の出力変動を保証したり、交流に変換してから電力系統に接続するなど、扱いには苦労します。
このため、1kW辺りにかかる発電の単価が、従来の石炭火力より高いです。
なお、詳しい発電原理は過去の記事をご覧ください。
太陽電池発電システム
大きく分けて、下記の2システム存在します。
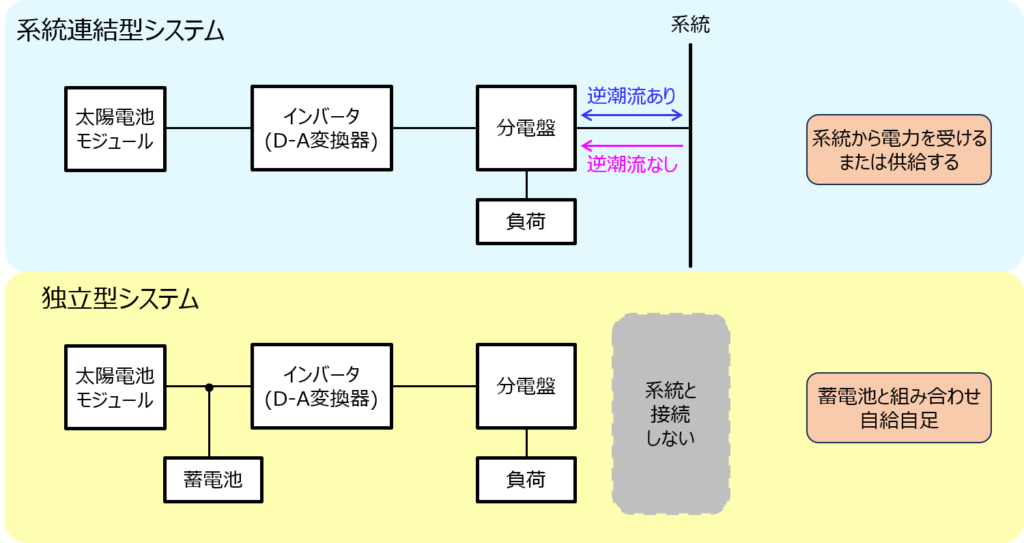
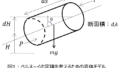
系統連結型システム
太陽電池を電力系統に接続するシステムです。これが最も多いです。余剰電力を売電したり、不足時は系統から電力を受けることができます。
下記の模式図を示します。太陽電池発電モジュールからDC→AC変換器(インバータ)を通し、版を通して系統に接続します。
盤には負荷も接続しています。負荷の消費電力以上に太陽電池が発電しているときは、系統へ逆潮流し、売電します。一方で、負荷の消費電力以下の時は、系統から電力を受けます。
独立型システム
太陽電池を系統に接続せず、独自の系統内で運転するシステムです。
負荷に対して電力が不足しているときは、その分を蓄電池から電力供給することで運転を継続します。
太陽電池モジュール
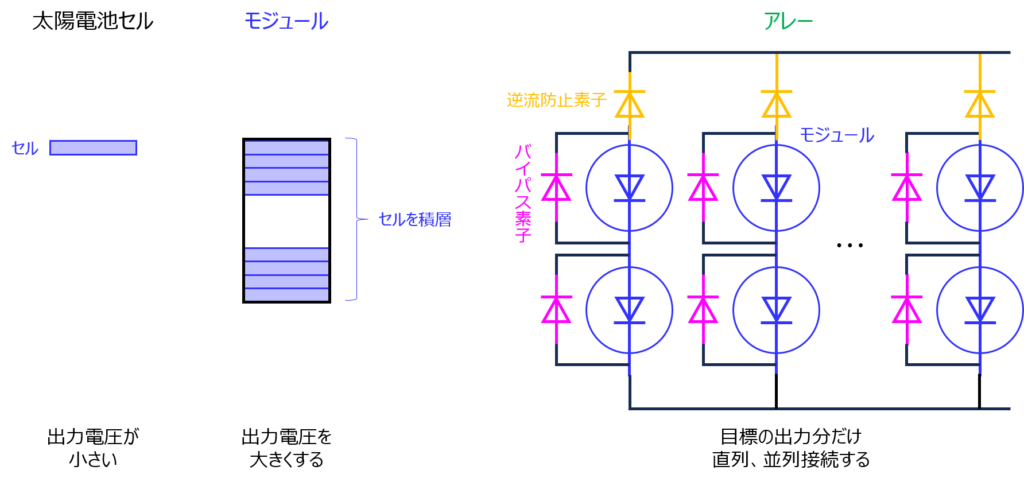
太陽電池の出力電圧は0.5V程度と、電気機器を動かすには低い電圧になっています。このため、太陽電池の発電セルを直列に接続し、動作電圧を高めます。
このように、発電セルの集合体をモジュールと言います。
一般的な家庭用太陽光発電機の場合、モジュールをさらに組み合わせ、アレーとして位置します。(下図)
太陽光電池の電流特性
問題文で示したように、I-V特性は(1)式、\(\exp\)項で表されます。
これは、pn接合から発生する順方向電流と短絡電流の和になります。
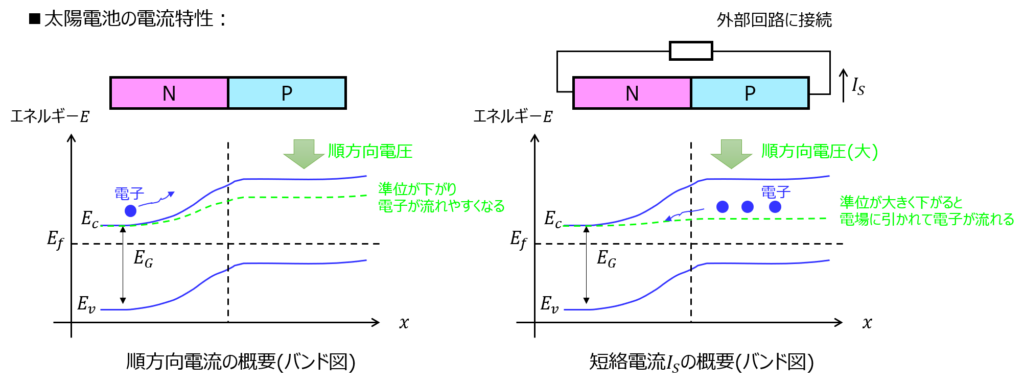
pn接合による順方向電流
過去の記事より、pn接合半導体には空乏層が発生しており、電場が発生しています。
電位差が発生するため、準位が異なります。(P側の準位が高い)
ここで、順方向電圧Vをかけると、P側の準位が下がり、電流が流れるようになります。
この式は、\begin{aligned}I=I_{0}\left(e^{\frac{eV}{k_{B}T}}-1\right)\end{aligned}
で表すことが出来ます。
一方で、外部回路に接続したときP領域から短絡電流\(I_{s}\)が発生します。これは、順方向に大きな電圧をかけると準位差が無くなりP型領域の電子がN領域に流れやすくなるためです。
これらを重ね合わせ、(1)式が得られるわけですね。
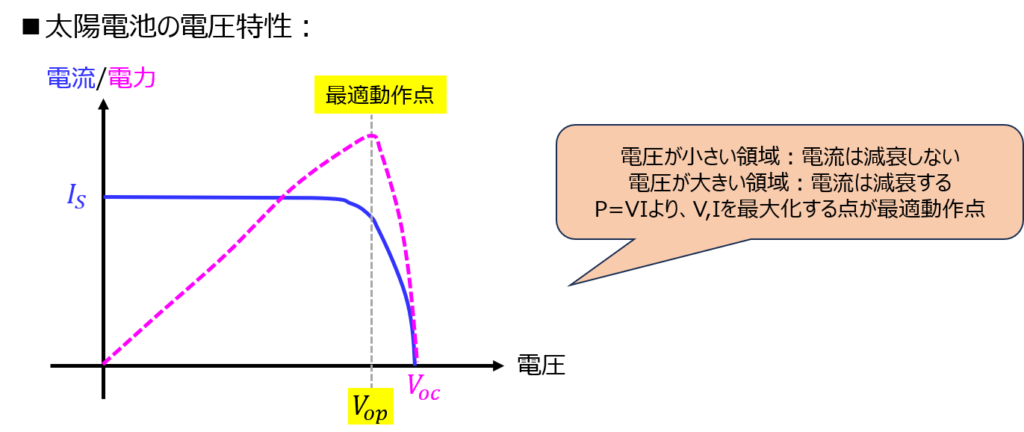
電圧が小さい領域においては定電流で流れ続けますが、一定値を超えると準位が崩れ、電圧が急激に下がります。
両者の丁度いい塩梅が最適動作点になります。
解答例
(a)(b) 電流-電圧特性、電力-電圧特性の概形
exp項に注目し、与えられた式(1)を図示すると、下図のようになる。
なお、電力-電圧特性は\(P=IV\)の関係を用いた。
(c) 最大効率
(b)より、電力の点線が最大を取る地点が最大効率になります。
そのため、下記の条件が成立するときに最大となります。
I-V特性の式の中で、ある電圧Vを決め、その時の電流Iを計算的に求める。
\(P=VI\)の式を考え、\(P\)を最大化する\(V_{op}\)が最大。
参考文献
電気エネルギー工学 八坂 保能(編著) P80,81