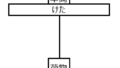
直流電動機とは
1極の界磁磁場に対し、回転子が回ることで誘導起電力が発生。その時に流れる電流から発生する電磁力により、回転する電気機器です。
過去の記事では、誘導機や同期機を説明してきました。三相での使用が主でしたが、直流機の場合は一相での使用が主です。
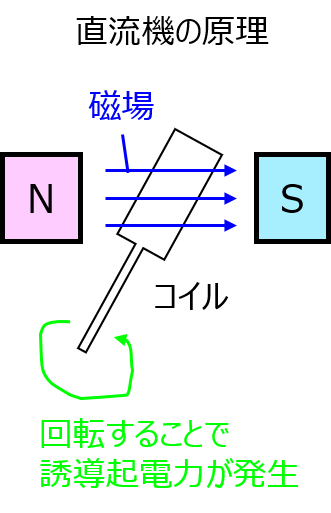
直流機の構成
誘導機、同期機同様に、磁場を発生させる界磁、回転し、誘導起電力を発生する電機子から構成されています。他、回転子の電機子巻線で発生した交流電圧を整流し、直流として外部に取り出すブラシ(整流子)が存在します。
ブラシには、一般的に黒鉛がよく使われます。適度な抵抗と強度を持っており、摩擦係数も小さく安価であるためです。
電機子反作用
同期発電機の記事でも説明しましたが、直流機でも発生します。(詳しくは、リンク先を参照ください。)
対策として、補償巻線による電機子磁場の打消しがあります。電機子と直列に接続し、電機子から発生した電流を逆向きに流すことで、電機子反作用を低減する効果があります。
直流機の種類
下記4種類存在します。
| 方式 | 種類 | 界磁 | 備考 |
| 他励式 | 他励発電機 | 外部電源から供給 | – |
| 自励式 | 分巻発電機 | 自身の持つインダクタ回路の 誘導起電力から発生 | 界磁巻線と負荷が並列 |
| 自励式 | 直巻発電機 | 上と同じ | 界磁巻線と負荷が直列 回転速度は電機子電流に反比例する |
| 自励式 | 複巻発電機 | 上と同じ | 分巻と直巻両方の回路構成 |
他励機
下記に他励発電器の回路構成を示します。前節の表のように、界磁は外部電源から供給し、その磁場を用いて2次側の発電機が回転する方式になっています。
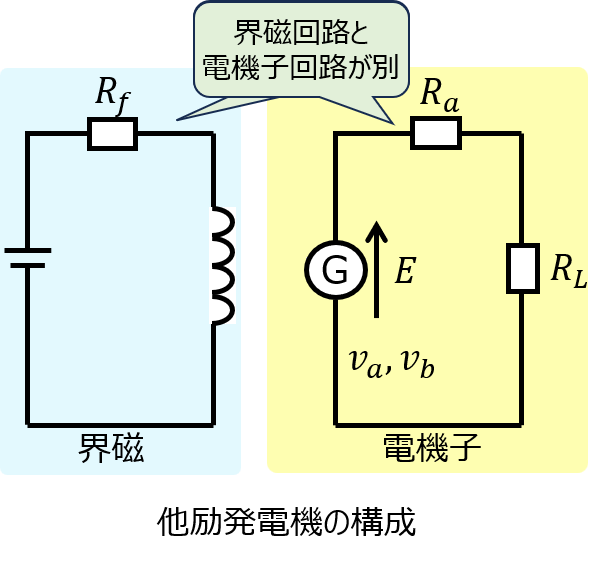
発電機の誘導起電力を\(E\)電機子反作用による電圧降下を\(v_{a}\)、ブラシ接触による電圧低下を\(v_{b}\)とすると、端子電圧\(V\)は下記の式で表されます。
\begin{aligned}V=E-(R_{a}I+v_{a}+v_{b})\end{aligned}
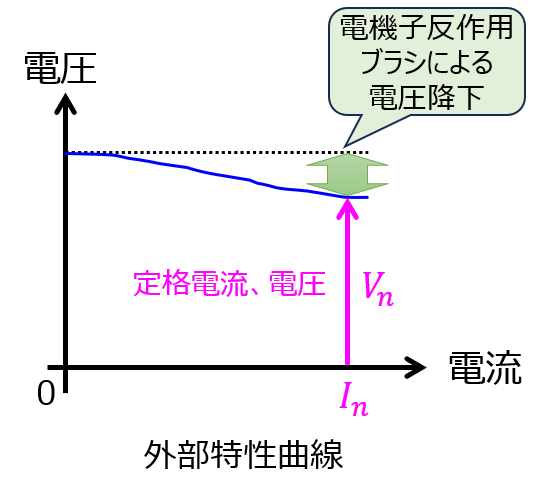
この結果、負荷電流に対する端子電圧の関係(外部特性曲線)は下記のようになります。負荷電流を増加するほど、端子電圧が降下していきます。
また、無負荷飽和曲線は下記のようになります。界磁電流を増加するほど発電機の誘導起電力は増加するものの、一定以上になると飽和します。これは、発電機に内蔵する鉄心の磁気飽和によるものです。
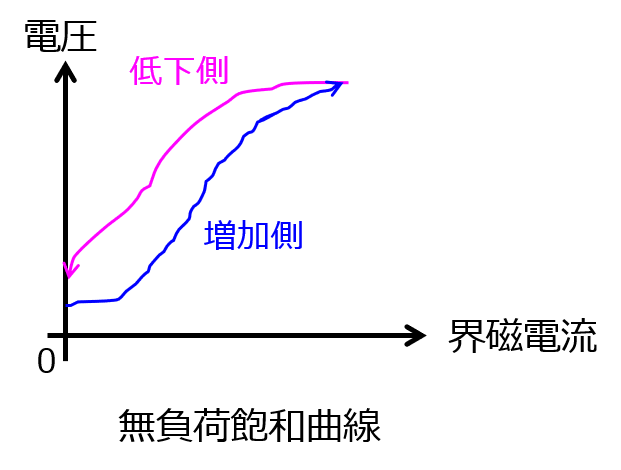
その後、界磁電流を減少させたときは、鉄心の残留磁気による影響もあり、誘導起電力は界磁電流を大きくした時よりも大きい値で低下していきます。
トルクと回転速度
トルクについては、下記式で表すことができます。(\(K\)は定数。)
\begin{aligned}T=K\Phi I_{a}\end{aligned}
また、回転速度については
\begin{aligned}N=\dfrac{V}{K\Phi}\end{aligned}
で表され、磁束\(\Phi\)が一定ならば、回転速度は電機子電圧\(V\)に比例します。
広い範囲でトルクと回転速度を制御できるため、圧延機の駆動などに使用されてきました。
他励式発電機の例題
負荷電流200A、端子電圧200V、電機子抵抗0.1Ω回転速度1500rpmで運転中の他励発電機が有る。この発電機の負荷電流および界磁電流を一定に保ったまま、回転速度を1200rpmに低下させた。低下させる前後の誘導起電力の値をそれぞれ求めよ。
<解答>
与えられた回路より、回転速度を低下させる前の誘導起電力\(E_{1}\)は
\begin{aligned}E_{1}&=V+R_{a}I \\ &=200+0.1*200 \\ &=220[V]\end{aligned}
界磁電流は一定なので\(\Phi\)は一定。前節より、電機子電圧は回転速度に比例する。
よって、回転速度を低下させた後の誘導起電力\(E_{2}\)は
\begin{aligned}E_{2}=220*\dfrac{1200}{1500}=176[V]\end{aligned}
分巻機
下記に分巻発電機の回路構成を示します。自励式のため、発電機自身から発生する誘導起電力から発生する電流により界磁を発生します。
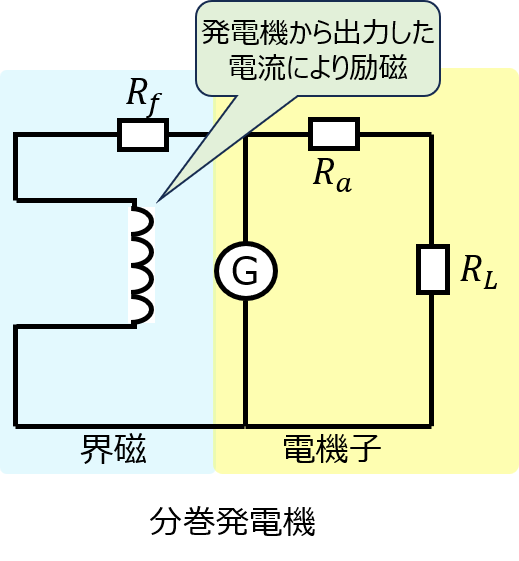
\(v_{f}\)を界磁電流\(I_{f}\)の減少による電圧降下とすると、端子電圧と負荷電流の関係は下記の式になります。
\begin{aligned}V=E-(R_{a}I_{a}+v_{a}+v_{b}+v_{f}\end{aligned}
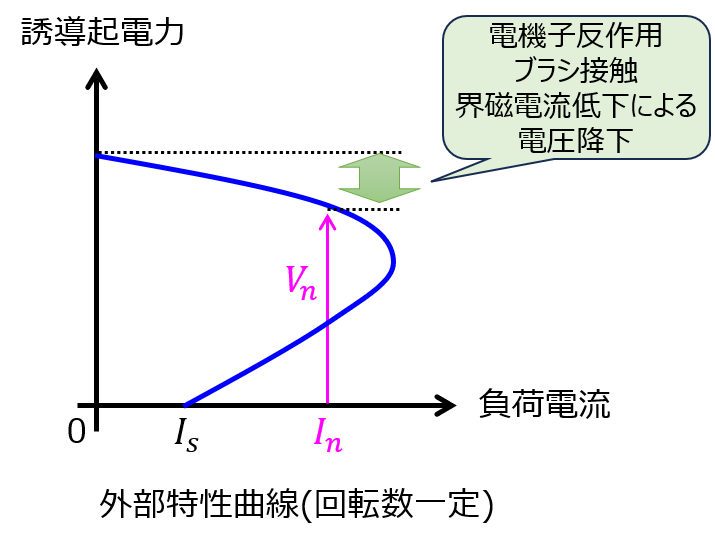
これから、外部特性曲線は下記のようになります。
トルクと回転速度
\begin{aligned}T=K \Phi I_{a}\end{aligned}
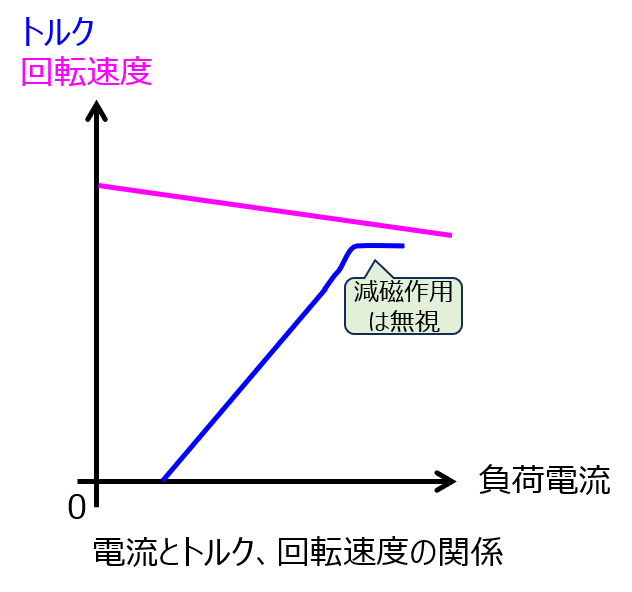
で表されます。電機子電流に対して1乗に比例します。
負荷が小さい範囲では電機子電流に比例して変化しますが、それ以上の範囲になると電機子反作用(減磁作用)が増して発電器への鎖交磁束が減少するため、トルクは小さくなります。
\begin{aligned}n=\dfrac{V-R_{a}I}{K\Phi}=V-R_{a}I\end{aligned}
なお、負荷電流が増加したとき、端子電圧および界磁電流が低下するため、他励発電機に対し負荷による電圧変動が大きくなります。
分巻機の例題
電機子抵抗が1Ω、電機子反作用、ブラシによる電圧降下がそれぞれ1Vの分巻発電機がある。定格回転速度で運転し、負荷抵抗10Ωを接続した。端子電圧を100Vとするために、界磁電流を5A流した。この時の誘導起電力と負荷電流の値を求めよ。なお、界磁巻線抵抗は無視できるとする。
<解答>
まず、負荷電流\(I\)は、\(V=IR\)より
\begin{aligned}I=\dfrac{100}{10}=10[A]\end{aligned}
電機子電流\(I_{a}\)は、\(I_{a}=I+I_{f}\)より
\begin{aligned}I_{a}=10+5=15[A]\end{aligned}
()式から、求める誘導起電力\(E\)は
\begin{aligned}E &=V+R_{a}I_{a}+1+1 \\ &=100+1*15+1+1=117[V]\end{aligned}
直巻機
同じく、下記に回路構成を示します。直列のため、(3)式の磁束\(\Phi\)が電機子電流\(I_{a}\)に依存します。このため、トルクは電機子電流の2乗に比例します。
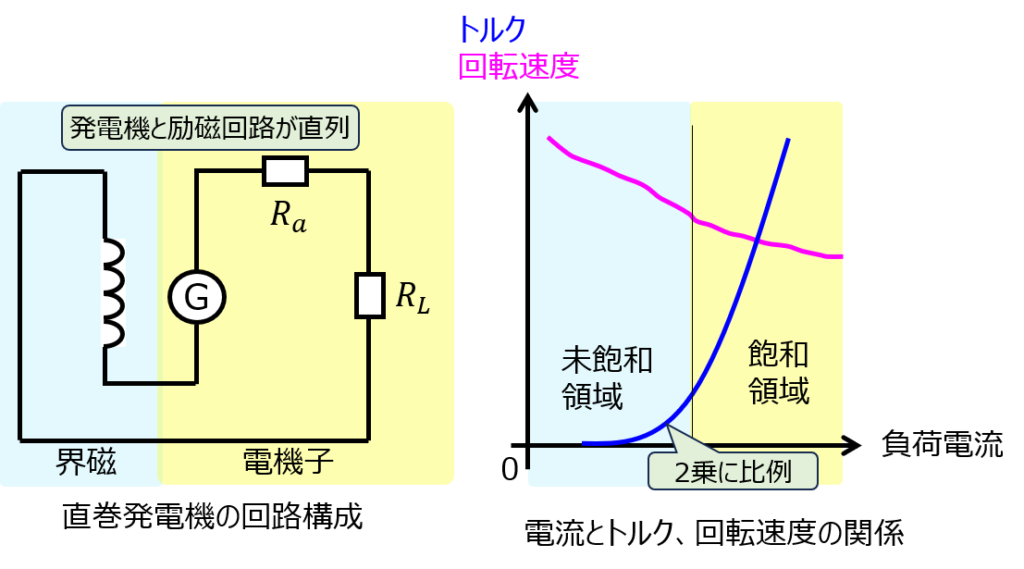
また、電機子抵抗を無視した時、回転速度は下記の式になります。
\begin{aligned}n=\dfrac{V-R_{a}I}{K\Phi}=\dfrac{V-R_{a}I}{I}=\dfrac{1}{I}\end{aligned}
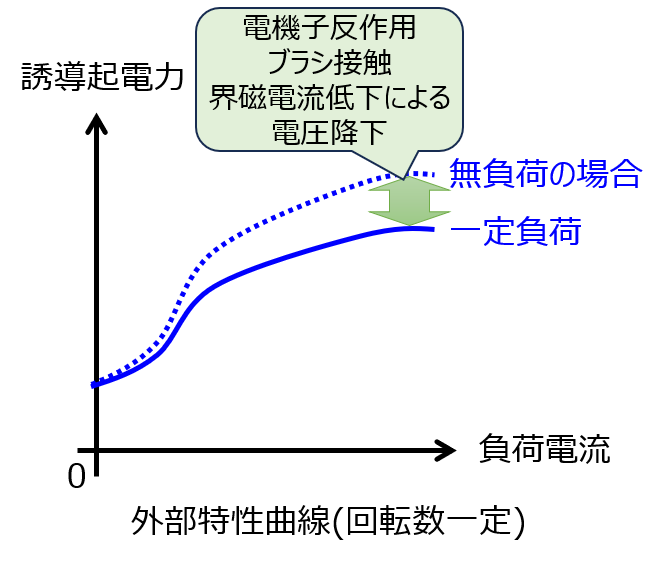
なお、回路の構成上、負荷を接続しなければ端子が開放になります。この場合、電流が流れないので界磁電流も0になります。
他方式と同じく、負荷を引いた際は電機子抵抗による電圧降下などで、誘導起電力は低下します。
直巻機の例題
電機子巻線抵抗および界磁巻線抵抗がともに0.1Ωの直巻電動機が有る。回転速度が1200rpmのとき、端子電圧が200V、電機子電流が100Aだった。この電動機の誘導起電力を求めよ。
<解答>
今回は、発電機ではなく電動機に関しての問題です。発電機の場合、負荷に電力を供給します。よって、負荷にかかる電圧は誘導起電力に対して小さいです。
一方で、電動機の場合は、一次側から電圧(端子電圧)を供給し、その結果発生する電機子電流、磁界によって動作します。よって、誘導起電力は、端子電圧に対して電機子電流による電圧降下を引き算します。
落ち着いて回路を書けばやることは変わりません。発電機/電動機、動き方問わずモータ自身の誘導起電力を求めることが、一貫してやるべき計算です。
電動機の誘導起電力\(E\)は
\begin{aligned}E=220-(0.1+0.1)*100=200[V]\end{aligned}
<補足>
答えとしては上記になりますが、電験ではここからトルクを求めさせることが多いです。
\begin{aligned}P=\omega T=EI_{a}\end{aligned}
の関係式を用いて
\begin{aligned}T=\dfrac{200*100}{2*\pi*1200/60}= 159 N・m\end{aligned}
と計算できるところまで覚えておきましょう。
複巻機
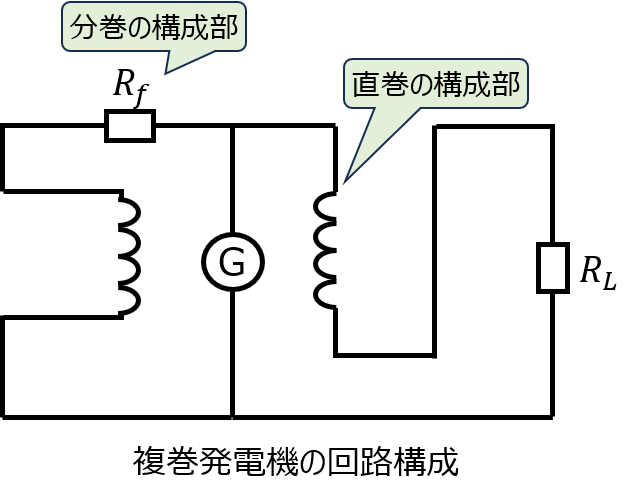
分巻と直巻、両方の構成で励磁する直流機を言います。この結果、負荷電流に対する発電機(複巻)のトルク、回転速度の関係は、両者を按分したものになります。
なお、直巻と分巻分のコイルから発生する磁束の和が足し合わされる側になる場合を和動複巻発電機と言い、引き算になる場合を差動複巻発電機と言います。
また、負荷の大きさを変えてもほぼ一定の端子電圧を持つ場合を平複巻発電機と言い、端子電圧が増加する場合を過複巻発電機と言います。

複巻機の例題
電機子抵抗が0.05Ω、分巻界磁巻線抵抗が40Ω、直巻界磁巻線抵抗が0.25Ω、界磁抵抗が20Ωの複巻発電機が有る。負荷電流が40A、端子電圧が100Vのとき、発電機の誘導起電力と電機子電流の値を求めよ。
なお、電機子反作用による電圧低下、ブラシ接触による電圧降下をそれぞれ1Vとする。
<解答>
分巻側の端子電圧\(V_{f}\)は
\begin{aligned}V_{f}&=V+R_{2}I \\ &=100+0.5*40 \\ &=120[V]\end{aligned}
これより、界磁電流\(I_{f}\)は
\begin{aligned}I_{f}=\dfrac{V_{f}}{R_{f}+R_{1}} \\ &=2[A]\end{aligned}
電機子電流\(I_{a}\)は
\begin{aligned}I_{a}&=I+I_{f} \\ &=40+2 &=42[A]\end{aligned}
以上より、求める誘導起電力\(E\)は
\begin{aligned}E&=V+(R_{a}I_{a}+R_{2}I+1+1) \\ &=100+(0.05*42+0.01*40+1+1) \\ &=104.5[V]\end{aligned}
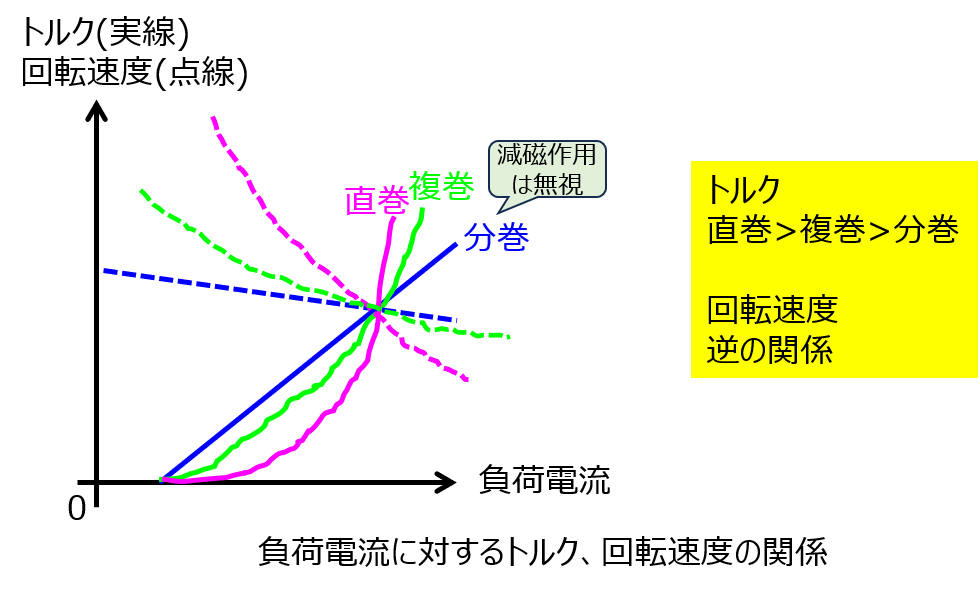
自励式発電機のトルク、回転速度の特性
前節までの内容を総合すると、下記のようになります。負荷電流を大きくすると、直巻/分巻発電機のトルクが最大/最小になる一方、回転速度に関してはそれぞれ最小/最大になります。
最後に
直流機は、院試ではあまり出題は無いものの、電験では毎年出題されます。将来、電力系統に関わる業務に携わりたい方は、是非ともマスターしましょう。