調速機による負荷変動のフィードバック制御を考える。電力系統の微小変動時、下記の運動方程式で表されるとする。ただし、\(M\)は慣性定数、\(\Delta P_{m}\)は、発電機の機械出力、\(\Delta P_{e}\)は負荷の電力変化を指す。負荷の電力変化\(\Delta P_{e}\)をステップ状に与えた場合を仮定し、下記の問いに答えよ。
\begin{aligned}M\dfrac{d\Delta f(t)}{dt}=\Delta P_{m}(t)-\Delta P_{e}(t)\end{aligned}
(1)調速機が存在しない場合の周波数偏差の時間変化を考えよ。
(2)調速機が存在する場合の周波数偏差の時間変化を考えよ。ただし、フィードバックゲイン\(K\)を仮定して良い。
なお、簡易的に発電機の機械出力と電気出力は等しいとする。
調速機(ガバナ)とは
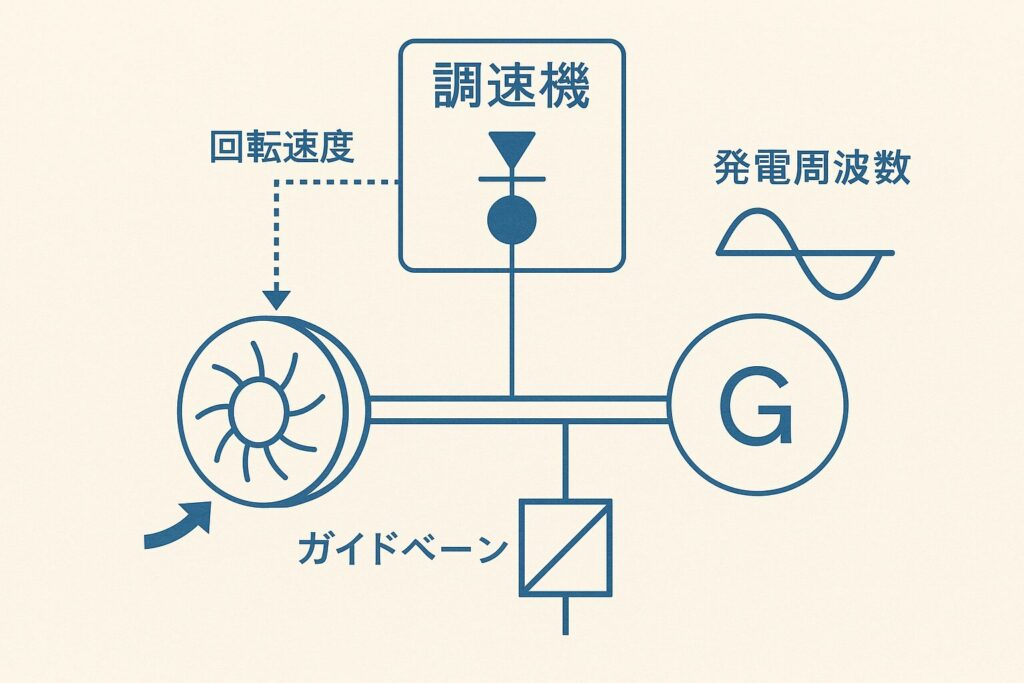
発電機の回転周波数(発電周波数)を一定に保つための制御装置を言います。電力系統は、需要と供給が常に一致している必要があります。この関係を発電機に落とし込むと、発電機の機械出力\(P_{m}\)と需要家側の負荷消費\(P_{e}\)が等しくなります。
需要の方が大きくなった時は消費の方が大きくなるわけですから、\(P_{m}<P_{e}\)になります。このとき、発電周波数は低くなります。(低下)
逆に、供給の方が大きくなった時は\(P_{m}>P_{e}\)になります。このとき、発電周波数は高くなります。(上昇)
需要と供給と周波数のイメージ
\(P_{m}<P_{e}\)のとき、なぜ周波数が低下するのか、イメージを説明します。
自転車で考えると分かりやすいです。人がペダルをこぐ仕事を\(P_{m}\)、道の高低により、一定速度で巡行するために必要な出力を\(P_{e}\)とします。始めはある角度の上り坂を一定速度で巡行しており、\(P_{m}=P_{e}\)とします。
上り坂が急になった時は\(P_{e}\)が大きくなります。こぐ力\(P_{m}\)を上げないと、車輪の回転速度が落ちていき、やがて止まってしまいます。これが周波数の低下と紐づいています。
上り坂がなだらかになった時は\(P_{e}\)が小さくなります。こぐ力\(P_{m}\)を下げないと、車輪の回転速度が上がり過ぎて制御できなくなります。これが周波数の上昇と紐づいています。

このように、日常の生活と電気-機械の出力関係を連想していくと分かりやすいです。
発電所における周波数調整方法
前節の説明のように、電気的出力(需要)が高くなった時は機械的出力を上げれば良いです。よって、水力発電所の場合は水車に送る水量を下げると良いです。また、火力発電所の場合は、タービンに送る蒸気量を減らせば良いです。
需要が低くなった時は、上記と逆のことをすれば良いです。
負荷の自己制御性
前章より、需要と供給の関係次第では発電周波数が変動することを説明しました。フィードバック制御をし適切な周波数に戻すことが必要ですが、電力系統に接続する負荷の特性により、ある程度の周波数変動ならば自然とフィードバックがかかる現象を負荷の自己制御性と言います。
例えば、供給が需要より大きくなった時、発電機の周波数は高くなります。系統に接続する負荷が誘導電動機などの場合、回転数が高くなると\(P=\omega T\)の関係により、消費電力\(P\)が大きくなります。需要が大きくなるフィードバックがかかることと同義ですから、周波数が低下する側(安定側)に働きます。
負荷の変動周期に応じて、下記のように制御の分担をしています。

ガバナフリー運転
周波数変動に応じて、ガバナが自由に出力を調整できる運転方式を言います。外部からの出力指令に固定されず、自律的に運転できることから、標記の呼ばれ方をしています。
瞬時の応答性に優れる利点があります。一方で、燃料制御が複雑になることや、発電所側の発電計画とずれるリスクもあります。
解答例
周波数応答を手計算で検討するので、与えられた運動方程式をラプラス変換する。調速機が無い場合、ある場合それぞれについて考える。
(1)調速機が無い場合
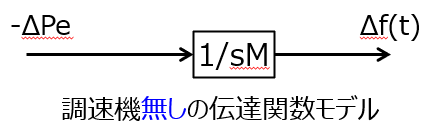
発電機の機械出力変化は発生しないので、\(\Delta P_{m}(t)=0\)。この時の(1)式は
\begin{aligned}M\dfrac{d\Delta f(t)}{dt}=-\Delta P_{e}(t)\end{aligned}
これをラプラス変換する。\(\Delta P_{e}(t)\)はステップ関数であることに注意し
\begin{aligned}Ms\Delta F(s)=-\dfrac{\Delta P_{e}}{s}\end{aligned}
\begin{aligned}\Delta F(s)=-\dfrac{\Delta P_{e}(s)}{sM}\end{aligned}
これをラプラス逆変換すると
\begin{aligned}\Delta f(t)=-\dfrac{\Delta P_{e}}{M}\end{aligned}
外乱により周波数偏差が発生し、時間が経っても解消されないことが分かる。
(2)調速機がある場合

機械出力\(P_{m}(t)\)にフィードバック要素\(-K\Delta f(t)\)を作用させる。同じくラプラス変換し
\begin{aligned}sM\Delta F(s)=-K\Delta F(s)-\Delta P_{e}(s)\end{aligned}
\begin{aligned}\Delta F(s)=-\dfrac{\Delta P_{e}(s)}{sM+K}\end{aligned}
ラプラス逆変換すると
\begin{aligned}\Delta f(t)=-\dfrac{\Delta P_{e}(s)}{M}e^{-\frac{K}{M}}\end{aligned}
時間が経つと周波数偏差0になることが分かる。
最後に
調速機について、概要は説明しているものの、制御モデルを用いて数式で説明しているサイトが調べている限りなかったので作成してみました。もちろん、本当はもっと複雑な伝達関数を用いての話になると思われますが、まずは(1)式のような形で概要を数学的につかむことが重要です。