誘導電動機とは
外部磁界による誘導起電力により回転する電気機器を言います。用途ごとに構成の違いはあれど、様々な産業用機器に使用されています。
回転の原理
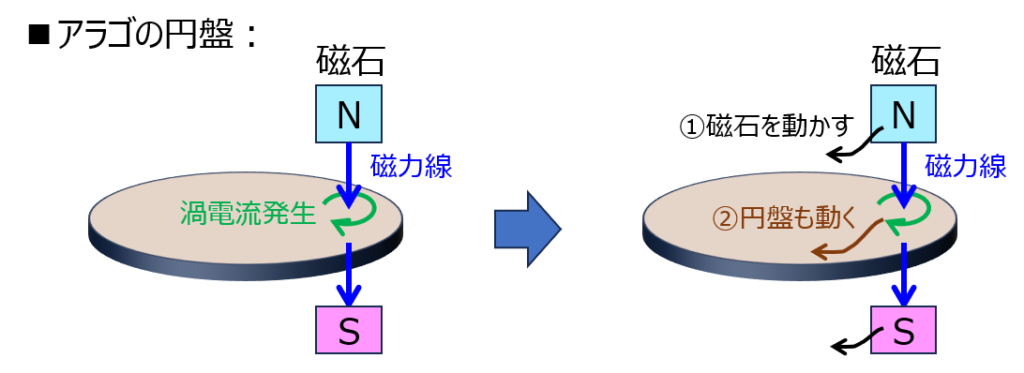
アラゴの円盤
原理を最も理解しやすい形になっています。円盤に対し、磁石を近づけ回転すると、誘導起電力により渦電流が発生します。
磁石の磁場と合わせると、電磁力が周方向に発生し、これにより回転します。
三相誘導電動機
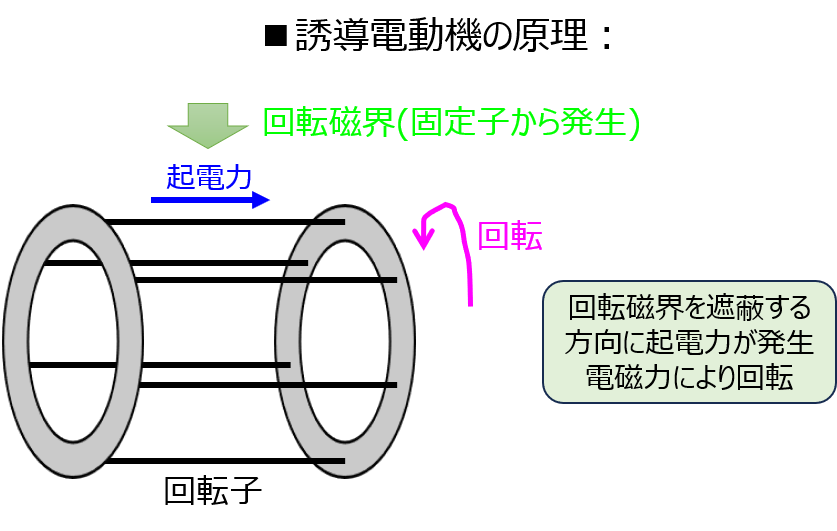
現実的には、磁石を手で持って高速で回転させることは困難です。そのため、磁石を物理的に動かさずとも、回転磁界を発生する方法を考えます。
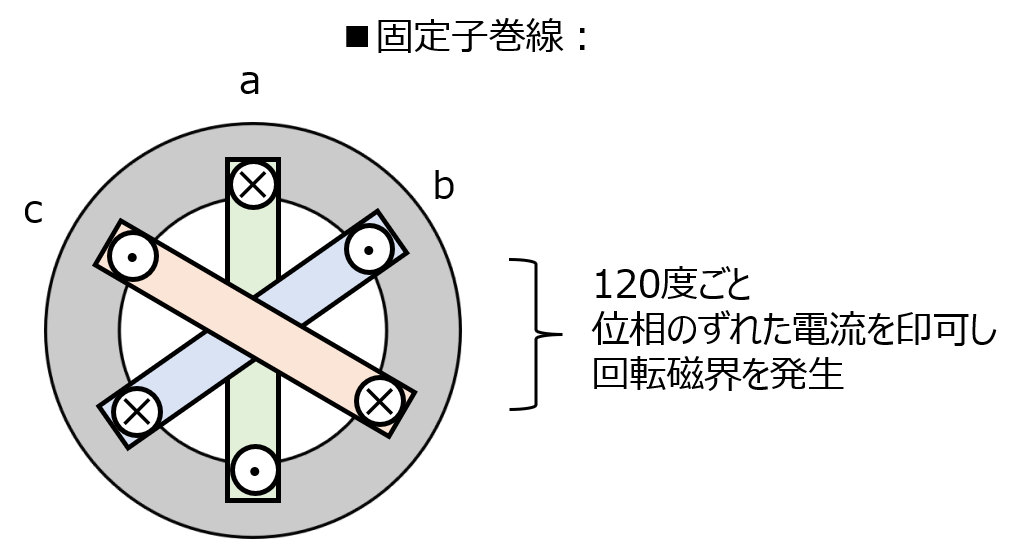
ここで考えられたのが、三つの固定子巻線に三相交流を流す方式です。位相が互いに120℃ずつずれており、この重ね合わせで全体としてみると磁場が回転しているように見えます。
これにより、電動機内部にある棒状の回転子に誘導起電力、誘導電流が発生。物理的に回転し続けることができます。
試験でも、本電動機を問われることが多いです。
誘導電動機の構造
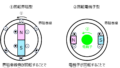
固定子
基本的な構成としては、前章(三相誘導電動機)で述べた内容と変わりません。ただ、渦電流損失を低減するため、鉄心は薄い鋼板を積層した形を取っています。
一つの鉄心の面積を小さくすることで、渦電流の流れる面積を小さくすることができます。
なお、小容量の電動機に対する固定子巻線には、ポリエステル線などの丸導線を用い、大容量の電動機にはガラス繊維巻の平角導線を用いることが多いです。
回転子
かご型回転子と巻線型回転子の2通りあります。

かご型回転子は、回転子の両端を短絡環を用いて短絡したものです。回転子付近の磁束密度を高め、トルクを高めること。機械的に丈夫になる利点があります。構造として簡単であるため、小容量の電動機によく用いられます。
反面、始動電流が大きく始動トルクが小さい欠点があります。
巻線型回転子は、短絡環を用いず、回転子に巻線を施した構成になっています。巻線に対し抵抗などの回路素子を接続することができるため、始動特性が高まります。
ただし、巻き線が絡まないようにするためスリップリングを別途設けるなど、複雑な構成になります。
誘導電動機の性質
同期速度とすべり
誘導電動機は、回転磁界に追従して動作する原理上、回転磁界の速度より回転速度が小さくなります。回転磁界の速度に対して足りない割合をすべりと言います。
回転磁界の周波数を同期速度\(n_{s}\)とすると、下記の式で表されます。
\begin{aligned}n_{s}=\dfrac{120f}{P}\end{aligned}
なお、\(f\)は回転磁界の周波数、\(P\)は電動機の極数を言います。問題次第では、”極対数”のパラメータを与えられることもあります。1極対=2極のため、この場合、(1)式の分子は60になることに注意しましょう。
電動機の回転速度を\(n\)とすると、すべり\(s\)は下記になります。
\begin{aligned}s=\dfrac{n_{s}-n}{n_{s}}\end{aligned}
sの値は、一般的に2~5%程度になることが多いです。また、あまり使われることはありませんが、電動機の回転速度が同期速度より速い場合は、誘導機は発電機として振る舞います。
動作周波数60Hz、極数が4の三相誘導電動機が1710[rpm]で運転しているとする。すべりはいくらになるか。
<解答>
与えられた誘導電動機の同期速度は、基本式\(n_{s}=\frac{120f}{P}\)より
\begin{aligned}n_{s}=\dfrac{120*6}{4}=1800[rpm]\end{aligned}
これより、求めるすべり\(s\)は
\begin{aligned}s=\dfrac{1800-1710}{1800}=0.05\end{aligned}
※解答冒頭で述べた基本式は、同期発電機のパラメータを求めるときにも使用します。過去の記事でも紹介しました。モータ全体で使用する式のため、暗記を推奨します。
誘導電動機の等価回路
変圧器の等価回路と似ています。変圧器は回転機では無いためすべりは発生しませんが、誘導機の場合はこの概念を回路上に表現する必要があります。
結論、2次側の負荷抵抗の部分がすべりの影響を受けます。
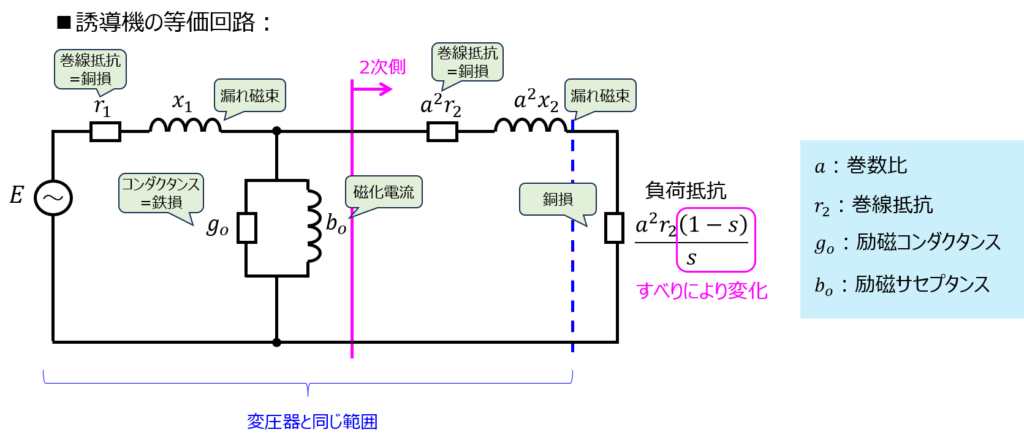
回転子が回転していない\(s=1\)のとき回路は短絡となり、回転するほど2次側の負荷が大きくなるイメージです。
誘導機の特性を確認したいときは、無負荷試験、拘束試験を行います。
誘導電動機の損失
変圧器にも鉄損、銅損があったように、電動機にも損失(機械損、鉄損、銅損)は存在します。
いま、誘導機が機械損の無い理想的な構成であるとすると、入力と損失はすべり\(s\)を用いて下記で表されます。
電動機への入力を\(P_{in}\)、二次銅損を\(P_{c2}\)、二次出力を\(P_{2}\)とすると
\begin{aligned}P_{in}:P_{c2}:P_{2}=1:s:1-s\end{aligned}
電動機の速度が大きくなるほどすべりが小さくなり、銅損が減少するイメージです。
なお、二次出力\(P_{2}\)は、定格出力+機械損で表されることが多いです。
問題文で機械損が与えられている場合は、加算を忘れないようにしましょう。
定格出力4kW、機械損が200Wの誘導電動機がすべり5%で運転しているとする。
このとき、二次出力\(P_{2}\)、二次銅損\(P_{c2}\)、一次入力\(P_{in}\)を求めよ。なお、鉄損は無視できるものとする。
<解答>
二次出力は、\(P_{2}=4000+200=4200[W]\)だから、(5)式より
\begin{aligned}P_{c2}=4200*\frac{0.05}{1-0.05}=221[W] \\ P_{in}=4200+221=4421[W]\end{aligned}
回転速度
誘導電動機が回転し始める時、すべりは\(s=1\)から始まります。このとき、2次側で誘導起電力が大きくかかるため、大きな電流が流れます。
一方で、始動がひと段落し、定格回転速度まで到達したときは、すべりは小さくなり、誘導起電力が小さくなります。このため、電流は小さくなります。
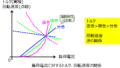
これを示したのが下記の図(電流-速度特性曲線)になります。
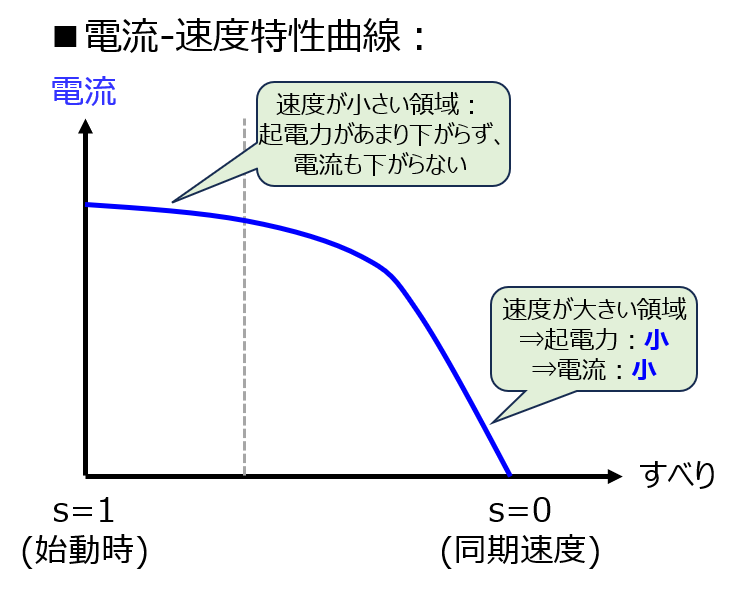
他、トルク\(T\)に関しては、\(P=\omega T\)と前章の等価回路の関係を考えることで
\begin{aligned}T=\dfrac{KE_{2}^{2}・\frac{r_{2}}{s} }{x_{2}^{2}+\left(\frac{r_{2}}{s}\right)^{2}}\end{aligned}
と表されます。(\(K\)は定数。\(r_{2},x_{2}\)は、2次側の抵抗、リアクタンス。)
トルクの最大化条件について、すべり\(s\)と誘導起電力\(E_{2}\)に注目します。
すべりが小さいほど、\(\frac{r_{2}}{s}\)が大きくなるが、誘導起電力\(E_{2}\)は小さくなるトレードオフの関係になっています。よって、両者の塩梅が最大トルク点になります。
(7)式を書き直して
\begin{aligned}T=\dfrac{KE_{2}^{2}・r_{2} }{sx_{2}^{2}+\left(\frac{r_{2}^{2}}{s}\right)}\end{aligned}
分母が最小になるためには、相加相乗平均の関係により、最大トルクになるための条件式は
\begin{aligned}\dfrac{r_{2}^{2}}{s}=sx_{2}^{2} \end{aligned}
比例推移
(7)式をもう一度見てみましょう。トルク\(T\)は2次側抵抗\(r_{2}\)に依存します。
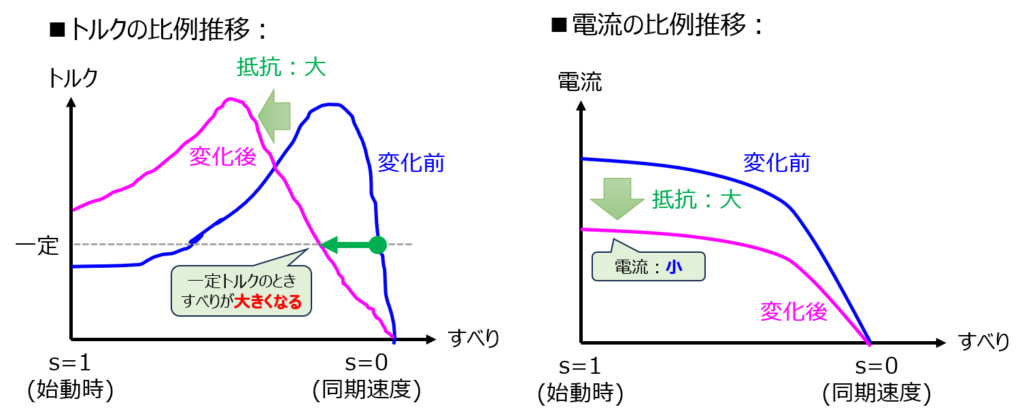
と言うことは、外部から抵抗を接続し、\(r_{2}\)を変化させてやれば同じトルクを出すためにすべりが変化することが分かります。これを比例推移と言います。
抵抗が大きくなる(負荷が大きくなる)ほど、回転数が小さくなり、すべりが大きくなるイメージです。(現実でも、平坦な道を自転車で漕ぐのと、坂道を漕ぐのとでは後者の方が負荷が高いです。よって、回転数が小さくなります。)
このとき、外部抵抗が大きくなるので、二次側の電流も同じく低下します。
<注意>
現実的には、巻線型誘導電動機に対して比例推移を考えます。かご型誘導電動機では、外部抵抗を物理的に接続できないためです。
一相分の巻き線抵抗が\(r_{2}=0.036[Ω]\)の巻線型三相誘導電動機が存在する。定格電圧、定格周波数の元で120%の始動トルクを発生させるために必要な外部抵抗を求めよ。
なお、定格負荷状態におけるすべりを\(s=0.03\)とする。
<解答>
比例推移より、120%のトルクを発生させるときのすべり\(s\)は
\begin{aligned}T:1.2T=0.03:s \Leftrightarrow s=0.036\end{aligned}
始動時のすべりは\(s=1\)なので、同じトルクを発生させるための外部抵抗\(R\)は
\begin{aligned}\dfrac{r_{2}}{s}=\dfrac{r_{2}+R}{1} \\ R=0.964[Ω]\end{aligned}
誘導電動機の速度制御
本節では、いくつか代表的な方式について説明します。
極数制御方式
(1)式より、誘導電動機の極数\(P\)を物理的に変更し、同期速度を変化させる方式です。極数は1,2,3の離散値を取りますので、同期速度も離散的に変わります。
主に、かご型誘導電動機で用いられます。
滑り調整制御方式
これは、前節で説明した比例推移の考えを利用します。
抵抗を接続することで、すべりが変化し、速度制御することができます。特に、始動時に用いられますが、銅損が大きくなるため、効率は悪いです。
周波数(V/f一定)制御方式
(1)式により、誘導電動機に対し回転磁界を変化させると回転数が変化します。インバータなどを用いて周波数を変化させます。
また、周波数を変化させた分、電圧も変化すると磁気飽和を防ぐことができ、継続運転できます。
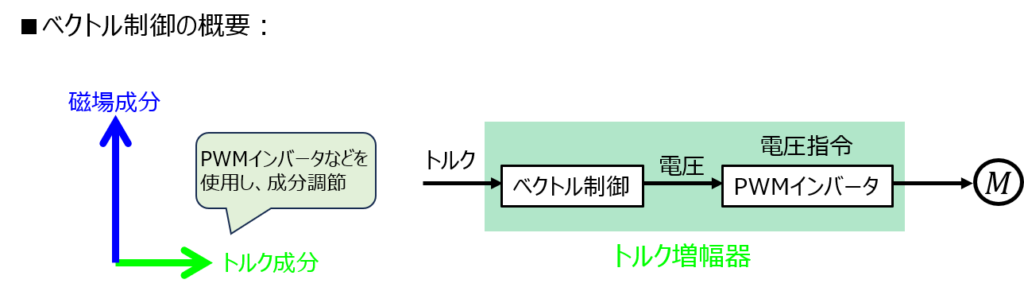
ベクトル制御方式
二次鎖交磁束を基準に、一次巻線に流れる電流を磁束成分とトルクを発生させる成分に分解し、それぞれを制御する方式です。制御機器には、PWMインバータを用いた電圧指令がよく使用されます。
それぞれのベクトル成分を独立して制御することから、本命名となっています。
最後に
誘導電動機は、プラントや日常家電など、様々な現場で使用される電気機器です。私たちの生活に無くてはならないものです。
院試対策だけでなく、電験でも多数出題されます。
本記事では基本的な事項をまとめましたので、全て理解、覚えることを推奨します。