はじめに
電動機の種類と、その機械出力または電気出力を求める問題は電験の科目(機械)で毎年1,2問出題されます。
工場で電気設備設計をする上でも計算する場面があり、仕事をする上でも欠かせません。本記事では、電動機の種類をリストアップするとともに、動力を求めるうえでの計算式をまとめました。
機械出力の計算
電磁気学を勉強すると出てきますが、仕事の概念が重要です。
ある物体に力F[N]を加えて、1秒間にv[m/s]動かすときの機械出力\(P_{m}[W]\)は
\begin{aligned}P_{m}=Fv\end{aligned}
となります。回転機の場合は、トルク\(T[N・m]\)、回転速度\(n[1/s]\)を用いて下記のようになります。
\begin{aligned}P_{m}=2 \pi n T\end{aligned}
上記2つが基本になります。(1)式はまだしも、(2)式は人によっては覚えていない方も居るかもしれません。この機に是非覚えましょう。
電動機ごとの機械出力
- 揚水ポンプの電動機出力[kW]:\(P=\frac{9.8 Q H k}{60 \eta}\)
- \(Q:1分間の揚水量[m^3/min]、H:全揚程[m]、k:余裕係数、\eta:ポンプ効率\)
- 送風用電動機の電動機出力[kW]:\(P=\frac{q H k}{1000\eta}\)
- \(q:1秒間の風量[m^3/s]、H:風圧kPa、\eta:送風機効率、k:余裕係数\)
- 巻上機用電動機の電動機出力[kW]:\(P=\dfrac{9.8 m v}{\eta}\)
- \(m:巻上荷重[t],v:巻上速度[m/s]、\eta:巻上機効率\)
- 電車用電動機の電動機出力[kW](1台分):\(P=\dfrac{Fv}{N \eta}\)
- \(F:牽引力[kN]、v:列車速度[m/s]、N:電動機台数、\eta:動力伝達係数\)
揚水ポンプ
1.の分子は位置エネルギーmghに起因しています。1分間の揚水量\(Q\)に60秒を割ると1秒間の揚水量が出てくるわけですから、これをベースに瞬時出力[kW]を考えます。gは重力加速度で9.8[m/s^2]ですから、これらをmghに当てはめることで上式のようになるのですね。
たまに、余裕係数とポンプ効率を分子分母どちらに持っていけば良いか分からなくなることがあります。このときは、瞬時出力\(P\)が大きくなる側に配置すれば、間違えることはありません。(余裕係数は、その名の通り装置設計上の余裕度合いを設定するもので、一般的に1より大きいので分子に配置。効率は1より小さいので、分母に配置)
送風用電動機
2.の分子は圧力が流体にする仕事\(P dV\)に起因しています。流量=微小体積dVとみなせることから、提示したような式になっています。その他の考え方は1.と同じです。
巻上機用電動機、電車用電動機
3.は1.と殆ど同じです。1は、文字mが揚水量に対応していましたが、今回は巻上対象の物体の質量です。問題文で提示された値をそのまま代入すれば良いです。(ただし、単位には気を付けること。kg、gのオーダー違いなど)
4.は、前節で紹介した仕事の概念Fvをそのまま適用すれば良いです。電動機の台数分だけ、取り持つ仕事が分散するわけですから、N台あればその分を分母に入れることで1台分の出力を考えることができます。
機械効率について
前節で説明した式の分母には、●●効率などと効率を表す係数が有ります。これは、電動機出力を100%機械出力に使用できるわけでは無いからです。”機械”効率などと呼び方が変わる場合がありますので注意しましょう。
いずれも、先の式で求めた電動機出力に、機械効率分を除算した値が最終的な答えになります。(実質、余裕係数の一種になります。)
式ばかり紹介しても面白くないので、実際に例題を解いて確認してみましょう。
例題
揚水ポンプの計算問題
揚水ポンプを用いて、毎分20m^3の水を全揚程12m、有効落差11mの溜め池に揚水することを考える。ポンプ効率を0.85、余裕係数を1.1としたとき、必要な電動機出力[kW]を求めよ。
<解答例>
有効落差についてはひっかけです。あくまでも、揚水した水を発電に使用する際に利用できる位置エネルギー分を指しているのであって、揚水自体は全揚程踏まえて計算する必要があります。
このため、前章で説明した計算式から
\begin{aligned}P=\dfrac{9.8*20*12*1.1}{60*0.85}=50.7kW\end{aligned}
送風用電動機の計算問題
送風用電動機を用いて、毎秒10m^3の風量を1kPaの風圧で送風することを考える。機械効率を0.8、余裕係数を1.1としたとき、必要な電動機出力[kW]を求めよ。
<解答例>
単位に注意です。kWの出力を考える時、圧力はPa、kPaどちらで考えるのが正しいのか気になってしまうかもしれません。
この場合は、kPaで考えるのが正解です。kWで問われているのだから、kPaで考える。と覚えると良いかもしれません。問題で与えられた数値を素直に代入すれば答えにたどり着きます。
\begin{aligned}P=\dfrac{10*1*1.1}{0.8}=13.75kW\end{aligned}
巻上用電動機の計算問題
天井クレーンを用いて、30000kgの荷物を吊り上げることを考える。巻上速度を0.1m/sとする。この時、巻上用電動機の出力[kW]を求めよ。ただし、巻上機の効率を0.8、余裕係数を1.2とする。
同じく、公式に適用する値を精査する作業が必要です。与えた荷重はkgのため、t(トン)に換算しないとkWで求めることができません。30000kg=30t ですので、下記の計算になります。
\begin{aligned}\dfrac{30*9.8*0.1*1.2}{0.8}=44.1kW\end{aligned}
なお、問題によっては、引き上げ対象の荷物をkg、tと質量で与えることはせず、重力加速度9.8を掛けたN、kN(ニュートン)表記で問われることが有ります。(電車用電動機の式と同じになります。)このときは、9.8を再度掛けることは不要です。
その他、下記のようなエレベータ問題も出てくることが有ります。一緒に演習しておきましょう。
かご全体に加わる力が20kN、つり合いの重りに加わる力が5kNのエレベータがある。これを昇降速度0.4m/sで運転するとき、必要な電動機出力[kW]を求めよ。ただし、機械効率を0.8とする。
筆者はエレベータを設計したことが無いです。そのため、詳しい構造を知っているわけではありませんが、かごを単純に懸垂するわけではなく、重りを用いて上下する構造のようです。(下記)

そのため、重りは電動機が行う仕事を補助する立場にあり、その分だけ電動機が賄う仕事は減ると考える必要があります。20kNに対し5kNを減算した15kN分を電動機が負担する必要があるため、下記の計算式になります。
\begin{aligned}P=\dfrac{(20-5)*0.4}{0.8}=7.5kW\end{aligned}
補足
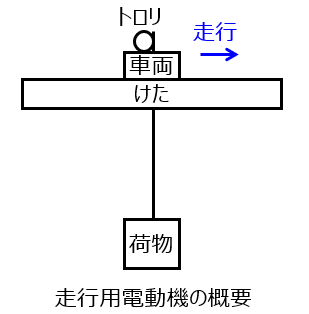
問題によっては、下記のようにクレーンの上に車両が存在し、左右に走行する場合も存在します。
トロリの重量を\(m_{2}\)、けたに加わる重量を\(m_{3}\)、走行抵抗を\(r\)[kN/kN]、走行速度を\(v\)[m/s]としたとき、必要な電動機出力は下記のようになります。
\begin{aligned}P=\dfrac{r(m+m_{2}+m_{3})*9.8*v}{\eta}\end{aligned}
電車用電動機の計算問題
ここまでくれば、公式を暗記していなくとも、物理的な動きをイメージできれば解答できるかもしれません。
電車の走行速度が30km/hで、10kNでけん引するとき、走行用電動機1台あたりの電動機出力[kW]の値を求めよ。ただし、機械出力を0.8とし、電動機の数を4台とする。
30km/hをm/sに単位変換する作業だけ注意が必要です。km⇒mには、10の3乗。1時間=3600秒であることから、h⇒sには、3600を割り算すれば良いです。
\begin{aligned}\dfrac{10*30*1000}{0.8*4*3600}=26kW\end{aligned}
最後に
厳密には、はずみ車に関する問題も出題されますが、、、出題頻度と公式を覚える時間のめんどくささから、筆者は捨てていました。
余裕のある方は覚えると良いかもしれませんが、そんな時間があるなら法規の完成度を上げる時間に費やした方が良いと思っています。公式については調べれば出てきますので、ここでは割愛します。