カウンタとは
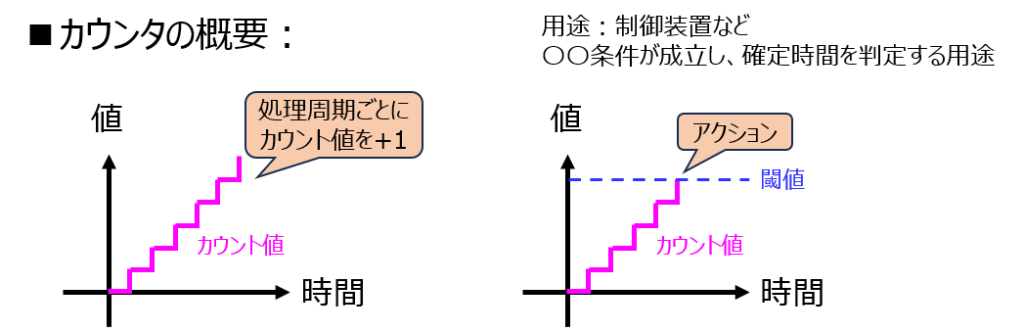
クロック(処理周期)のたびに、0→1→2→3→4、または4→3→2→1と数値を逐次加算/減算していく回路です。
前者はアップカウンタ。後者はダウンカウンタ(タイマ)と呼ばれています。
ストップウォッチ、制御装置など、あらゆる産業機器で使用されています。
このように、私たちの生活において身近に使用されている機器ですが、動作原理としては論理回路で説明することができます。
特に、院試ではDフリップフロップを用いてカウンタ作成をすることが多いです。
本記事では、最初にDフリップフロップの動作説明を行います。
その次に、代表的なカウンタの種類と回路の作成方法について取り上げていきます。
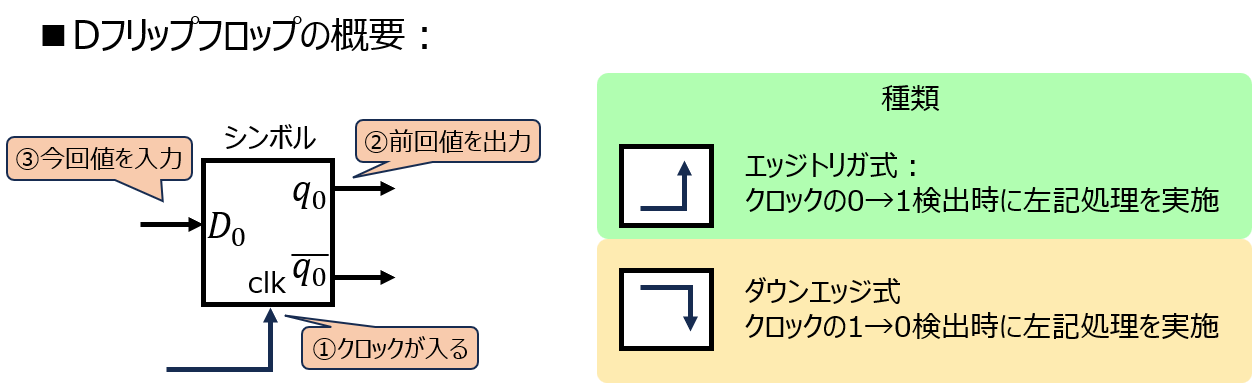
Dフリップフロップ(DFF)とは
1周期前の入力を保存する素子です。
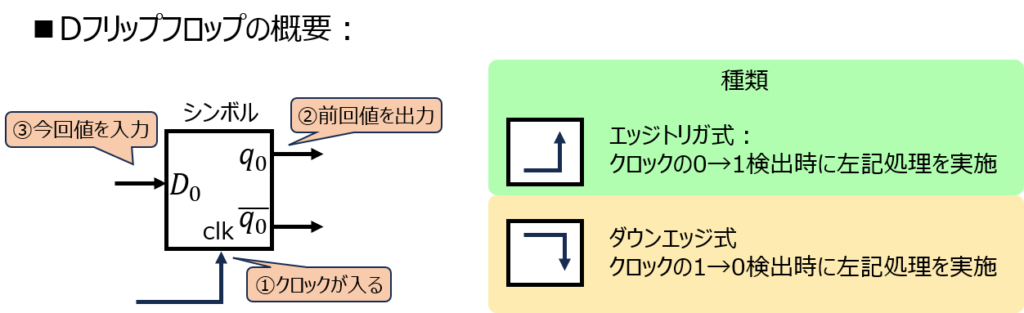
クロック入力が入った時(0→1)、入力されている値をDフリップフロップ内部に格納(更新)し、今まで入っていた値を出力します。
次回のクロック入力が来るまで格納した値は保持します。
ダウンエッジ型Dフリップフロップも存在し、この場合はクロック入力が取り下がった時(1→0)に上記の動作をします。
一般的にはエッジトリガ式(0→1)の方が多く使われます。本記事では、こちらを前提に説明を進めていきます。
6進アップカウンタ
0→1→2→3→4→5のように、初期値から6段階、クロックごとに加算し続けます。
6つの状態を区別しなければならず、過去の状態から1を加算して今回の状態を決定しなければならないです。
1つのDフリップフロップ(DFF)につき、0,1の2つの状態を区別できます。
よって、3つのDFFがあれば、最大\(2^{3}=8\)つの状態を区別することができます。6進カウンタを表現するためには、0~5の6つの状態を表現する必要があります。
これより、DFFが3つあれば6進カウンタを作成することができます。
3つのDFFを区別して\(D_{0},D_{1},D_{2}\)とし、それぞれの状態変数を\(d_{0},d_{1},d_{2}\)とします。
クロックが入った後の次の状態を\(q_{0},q_{1},q_{2}\)とします。
3つのDFFに入る値について、下記のように定義します。
0(10進数)→\((d_{2},d_{1},d_{0})=(0,0,0)\)
1(10進数)→\((d_{2},d_{1},d_{0})=(0,0,1)\)
2(10進数)→\((d_{2},d_{1},d_{0})=(0,1,0)\)
3(10進数)→\((d_{2},d_{1},d_{0})=(0,1,1)\)
4(10進数)→\((d_{2},d_{1},d_{0})=(1,0,0)\)
5(10進数)→\((d_{2},d_{1},d_{0})=(1,0,1)\)
いわゆる10進数→2進数の変換と同じように定義します。試験でも、同じように定義する問題が多いですが、\(d_{2}\)と\(d_{0}\)の対応が逆のこともあるので注意しましょう。
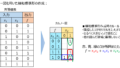
この考えを用いると、真理値表は下記のようになります。
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | clock | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
前述の通り、Dフリップフロップはクロック入力が入るまで値を前回値保持する素子です。
このため、真理値表を記載する上では、clock=1の表記は出来る限り行った方が良いです。(試験問題で省略しても良い条件文があるときを除く)
上記の真理値表ではclock=0の場合を省略していますが、前回値保持のため、\(d_{i}=q_{i}\)になります。(自明なので省略しています。)
\((d_{2},d_{1},d_{0})=(1,1,0),(1,1,1)\)の場合が定義されていないですが、ドントケア入力となります。(7進、8進カウンタになった場合は使用するので、この時は出力0,1が明確に決まります。)
真理値表を元に、各状態変数の論理式をカルノー図を用いて考えます。
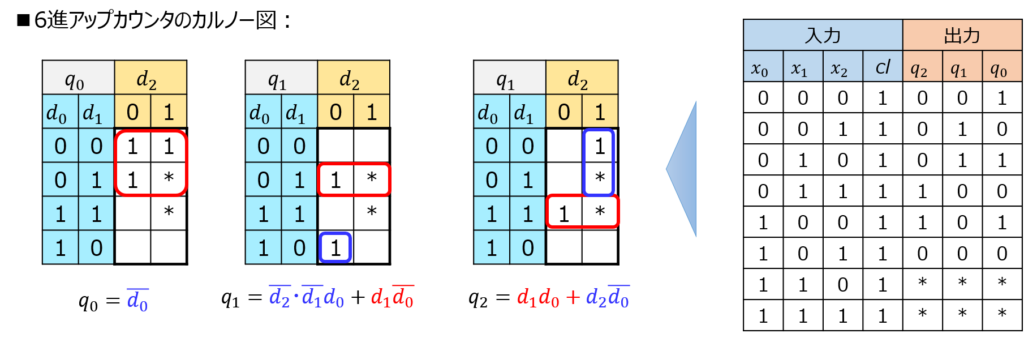
結局、下記のように表すことができます。
\begin{cases}q_{0}=\overline{d_{0}} \\ q_{1}=\overline{d_{2}}・\overline{d_{1}}d_{0}+d_{1}\overline{d_{0}} \\ q_{2}=d_{1}d_{0}+d_{2}\overline{d_{0}} \end{cases}
最下位bitの\(q_{0}\)はクロックが来るたびに1が入力されることを想定しているので、前回値に対し反転するシンプルな式となっています。
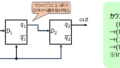
論理回路として表すと、下記のようになります。
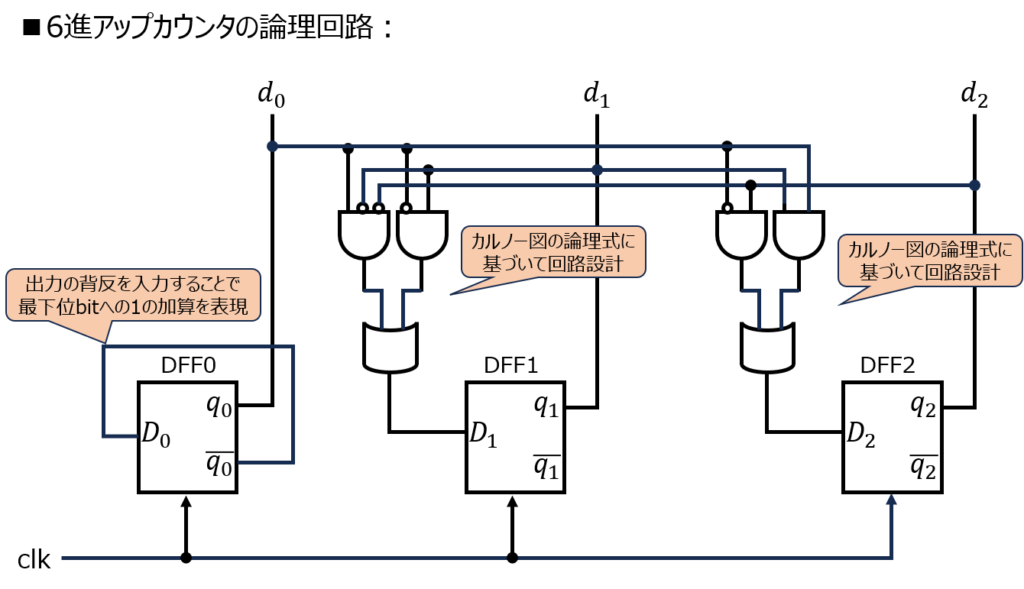
初期値としては、\(d_{0}=d_{1}=d_{2}=0\)の想定です。院試問題でも、特に断りが無ければ全て0の想定で回路を書いて良いと思います。
8進アップカウンタ (テクニック有り)
6進カウンタの真理値表に対し、ドントケアだった部分に明確な入出力を与えることで作成できます。
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | clock | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
同じくカルノー図を作成することで、6進カウンタと同じ手順で論理式を求めることはできます。
ただ、この作業をせずとも、下記の着眼点で論理式を書くことができます。
各状態変数\(q_{i}\)には、下記の性質があります。
- \(q_{0}\)は、クロックごとに必ず反転する。
- \(q_{i} \quad (i=1,2,\cdots) \)は、\(q_{0}=q_{1}=\cdots q_{i-1}=1\)のとき反転する。
1.については、6進カウンタで説明した通りです。実際の論理式でも(1)式のように示されています。
2.については、2進数の桁上げを考えると分かりやすいです。
\(q_{1}\)は、\(q_{0}=1\)の状態で1を加算すると\(q_{1}=1\)になります。
\(q_{2}\)についても同様に、\(q_{1}=q_{0}=1\)の状態で1を加算すると\(q_{2}=1\)になります。
\(q_{3}\)以上も同じことが言えるので、一般的に2.が成立します。
結局、下記の論理式になります。
\begin{cases}q_{0}=\overline{d_{0}} \\ q_{1}=d_{1} \oplus d_{0} \\ q_{2}=d_{2} \oplus d_{1}d_{0} \end{cases}
回路としては、下記で表すことができます。
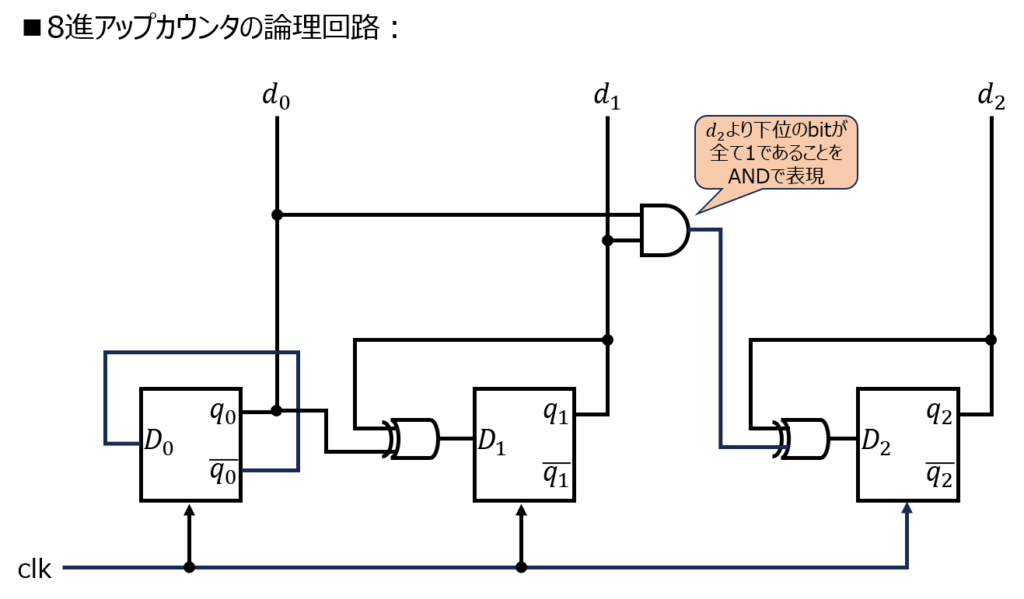
なお、この考え方(テクニック)は、\(2^{n}=2,4,8\)など、2の指数で丁度表すことができるカウンタに対して使えます。
6進、7進もリセット条件を頑張れば一部使える部分もありますが、その手間があるならばカルノー図からの論理式の簡単化を頑張った方が良いです。
8進ダウンカウンタ (テクニック有り)
同じ考えで、ダウンカウンタについても作成できます。
結局、真理値表さえ作成することができれば、後はその結果に基づいて論理式を求める流れに変わりが無いからです。(極論、ある数値ではアップしたり、別の数値ではダウンしたりする回路も設計できます。)
8進ダウンカウンタの真理値表は下記になります。
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | clock | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
同じく、カルノー図を書いて論理式を求めても良いのですが、アップカウンタと同様下記の規則性があります。
- \(q_{0}\)は、クロックごとに必ず反転する。(アップカウンタと同じ)
- \(q_{i} \quad (i=1,2,\cdots) \)は、\( q_{0}=q_{1}= \cdots q_{i-1} =0 \)のとき反転する。
2.だけアップカウンタと異なります。
あるbitが反転する条件は、アップカウンタでは下位のbitの数値が全て1でしたが、ダウンカウンタは全て0の時に反転します。
これは、10進数:4→3 ⇔ 2進数:100→011 を考えると分かりやすいです。
この規則性から、結局下記の論理式になります。
\begin{cases}q_{0}=\overline{d_{0}} \\ q_{1}=d_{1} \oplus \overline{d_{0}} \\ q_{2}=d_{2} \oplus \overline{d_{1}}・\overline{d_{0}} \end{cases}
排他的論理和の右側に入っている項にNOTが入るところが、アップカウンタとの違いです。
DFFの出力の\(\overline{q_{i}}\)の端子を活用することで、下記の論理回路になります。
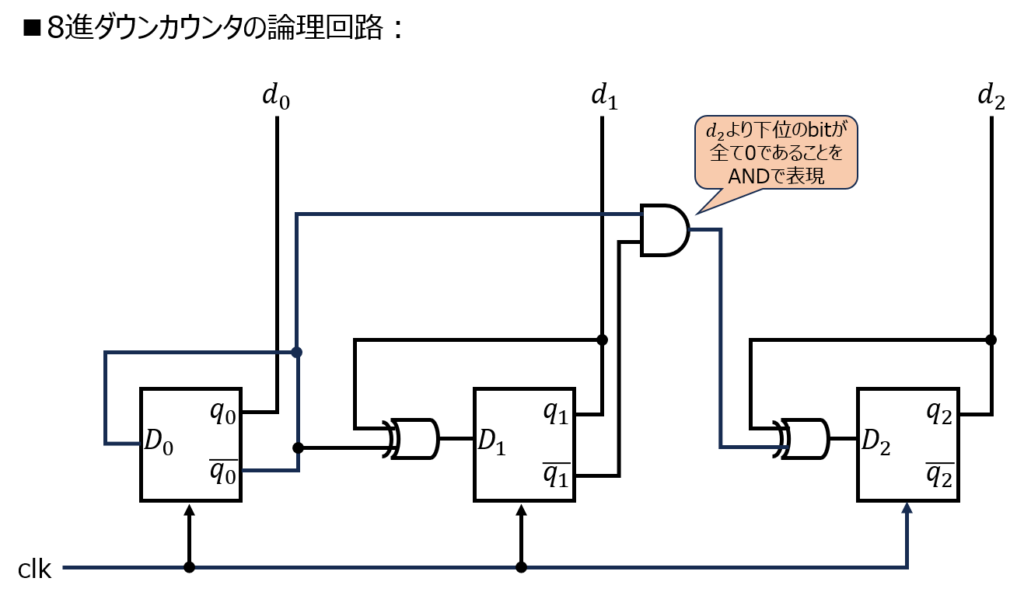
8進アップダウンカウンタ
今までの章で、アップカウンタとダウンカウンタそれぞれを説明してきました。
本章では、一つの回路でアップとダウン両方を表現できる構成を示します。
(2)(3)式より、排他的論理和の右側にNOTが入る/入らないでダウン/アップの計算を切り替えることができます。
ということは、アップ/ダウンを区別する入力\(u\)を定義し、\(u=1\)のとき加算。\(u=0\)のとき減算の想定で組むならば、下記の論理式で実現できます。
\begin{cases}q_{0}=\overline{d_{0}} \\ q_{1}=d_{1} \oplus (\overline{u} \oplus d_{0}) \\ q_{2}=d_{2} \oplus (\overline{u} \oplus d_{1})・(\overline{u} \oplus d_{0})\end{cases}
NOTを排他的論理和(XOR)で表現することがキーポイントです。
このようにすることで、回路を分けることなく、ただ入力\(u\)を切り替えることでアップダウンを切り替えることができます。
この考え方は加算、減算回路でも利用します。
論理回路としては下記になります。DFFの入力の手前にXORが追加になります。
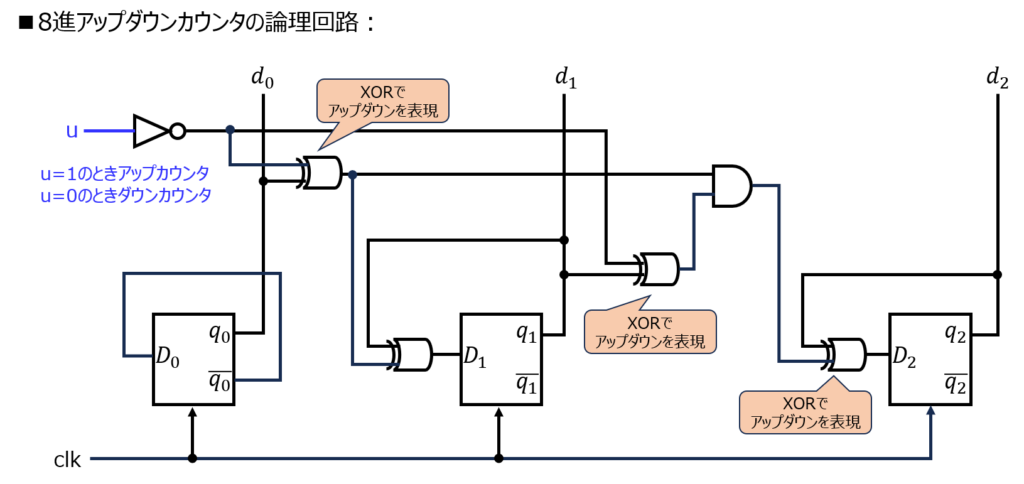
最後に
本記事を題材とした問題は、東大、京大、農工大、京工繊など様々な大学で出題されます。
テクニック部分の考え方も覚えると、大いに試験に役立つと思います。