シフトレジスタとは
クロックごとに、下位bitからその次の上位bitへ情報を伝搬する機能を持った回路を言います。
下記の図に概要を示します。左のDFFに格納された値をクロックごとに右に伝搬していく構造となっています。
1クロック目:入力x∊(0,1)がDFF0に入る
2クロック目:DFF0に入っていた入力x∊(0,1)がDFF1へ入る
3クロック目:DFF1に入っていた入力x∊(0,1)がDFF2へ入る
…
このようにして、クロックごとに値が上位のDFFへ伝搬(シフト)していきます。
そのため、シフトレジスタと呼ばれています。
シフトレジスタの用途
リレー形式のように、値が伝搬することから、シーケンサによく用いられます。
シーケンサとは、工場の制御装置でよく使われる機械です。決められた手順通りに命令をこなしていく役割を担っています。
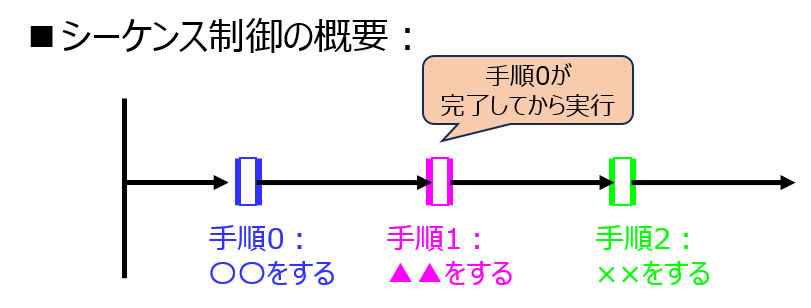
それぞれのDFFを手順0,1,2…と捉え、1が入っているDFFに対し、決められた手順を実行する手番を考えます。
最初に、手順0を示すDFF0に1を代入し、必要な作業を行います。
完了後、クロックを実行し、DFF1に1を代入すると、必要な作業を自動で行うことができます。
ある製品を製造する際、原料を混ぜる工程などで必ず順番があります。これを各DFFで区別するということですね。
シフトレジスタの真理値表、論理回路
ここまでの説明で察しが付いているかもしれませんが、下記になります。
(入力\(d_{i},clock\)、出力\(q_{i}\))
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | \(clock\) | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
※DFF0に対する入力は常時0の想定です。DFF2まで1が流れた後は全て0になります。
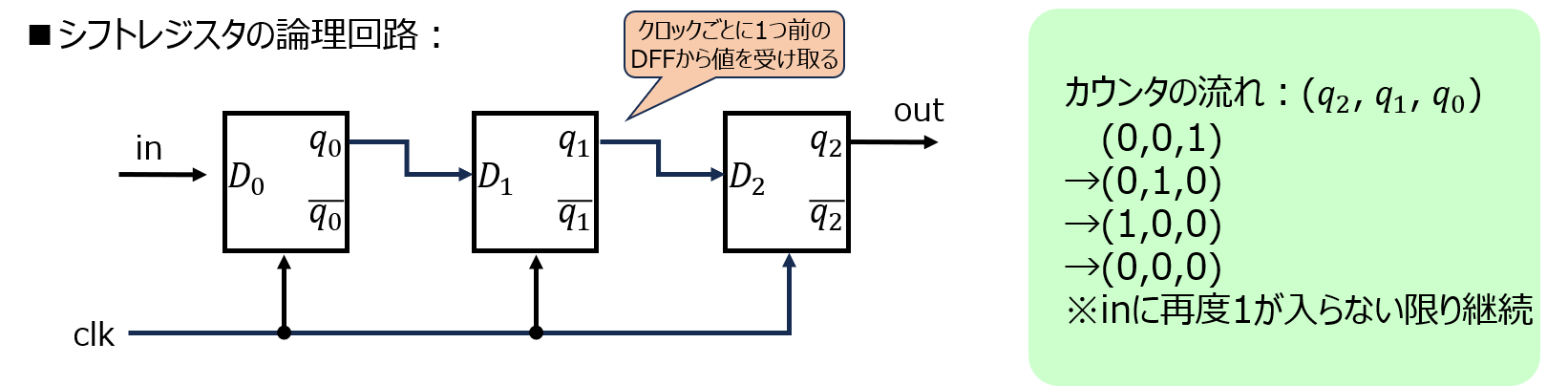
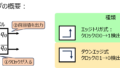
論理式としては次のように表されます。
\begin{cases}q_{1}=d_{0} \\ q_{i}=d_{i-1} (i=1,2,…)\end{cases}
このことから、回路構成も非常にシンプルです。
シフトレジスタの考えを用いたカウンタ
リングカウンタ
最後のDFFに1が入り、必要な作業を実行した後、同じ作業を繰り返したいこともあります。
その時は、最後のDFFの出力を最初のDFF0に入力することで、必要な作業をずっと行うことができます。
これをリングカウンタと言います。DFFがn個ならば、n個の状態を表現できます。
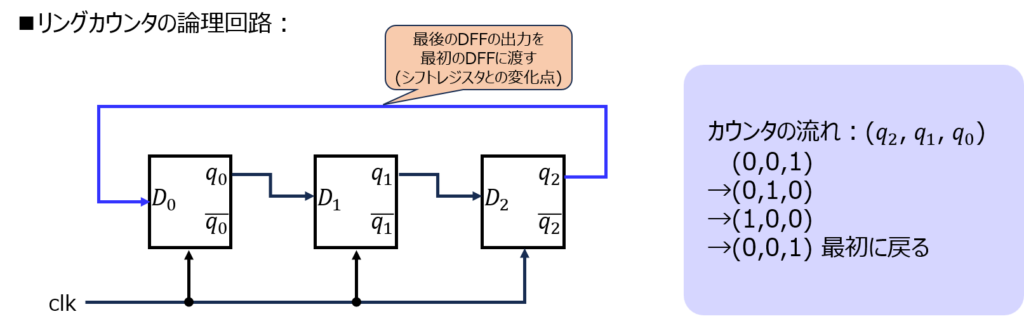
シフトレジスタでは、最上位bit(DFF2)に1が入った後は、DFF0に入力が来ない限りは全てのDFFに0が入り続ける仕様になっています。
一方で、リングカウンタはもう一度最下位bitに1が入り、ずっとカウントし続けることができます。
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | \(clock\) | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
\begin{cases}q_{0}=d_{n-1} \\ q_{i}=d_{i-1}\end{cases}
ジョンソンカウンタ
リングカウンタの派生です。
一番最後(右)にあるDFFのNOT出力を一番最初(左)にあるDFFに繋げるものです。
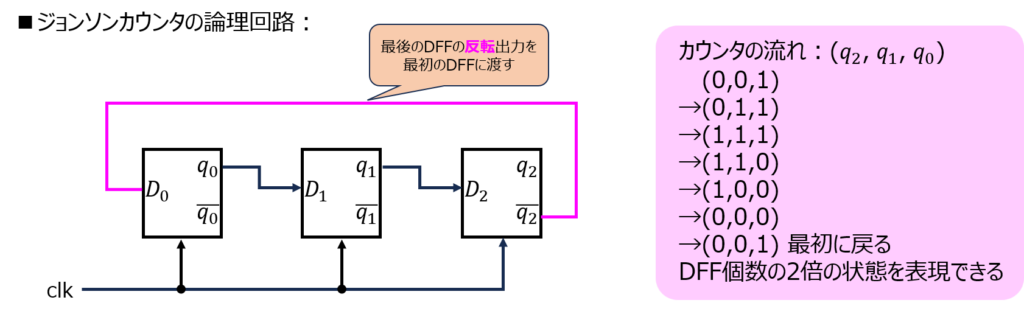
一番右のDFFが0である限り、一番左のDFFには1を入力し続けます。
一方で、一番右のDFFが1である限り、一番左のDFFには0を入力し続けます。
真理値表は下記のようになり、1になるDFFが複数個あることで2n個の状態を表現できます。
| \(d_{2}\) | \(d_{1}\) | \(d_{0}\) | \(clock\) | \(q_{2}\) | \(q_{1}\) | \(q_{0}\) |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
\begin{cases}q_{0}=\overline{d_{n-1}} \\ q_{i}=d_{i-1}\end{cases}
注意点
本記事では1bitのシフトを前提に説明していきました。
ですが、試験問題によっては一度に2bit伝搬する場合や、1が入っているDFFが1つではない場合もあります。
こういった場合は、真理値表を元に専用の論理式を求めていく必要があります。
最後に
本問は、京工繊でよく出題されます。
その他、DFFをよく出題する大学院(京大)でも出題される可能性があるため、考え方を理解しておきましょう。