グラフとは
点と辺からなる図形を言います。
数学的には、点集合\(V\)と辺集合\(E\)を合わせ、グラフGを下記のように表記することが多いです。
\begin{aligned}G=(V,E)\end{aligned}

グラフの種類
有名なものとして、下記のグラフがあります。
無向グラフ、有向グラフ
- 無向グラフ:点と点を結ぶ辺に向きが無いこと。
- 有向グラフ:点と点を結ぶ辺に向きが有ること。
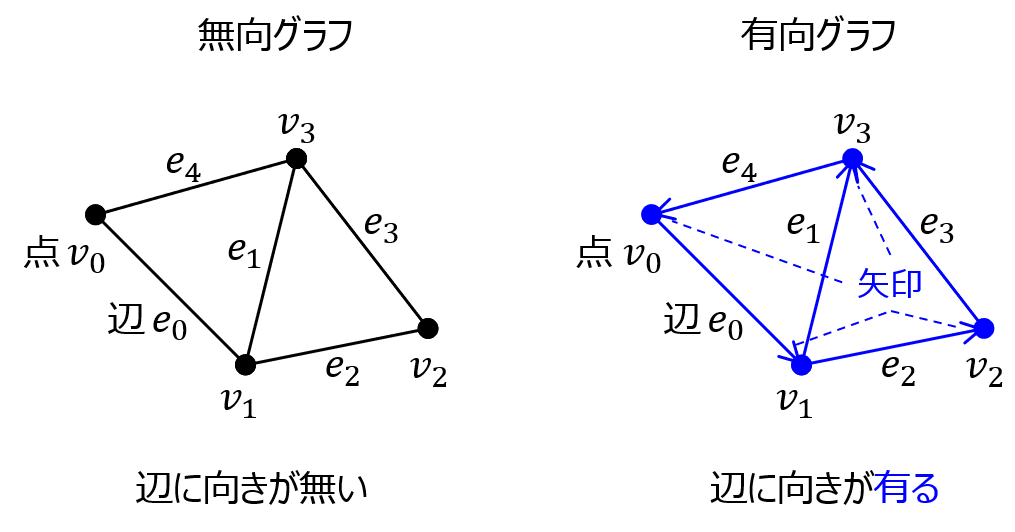
院試では、無向グラフが良く問われます。よって、本記事でも無向グラフに焦点を当てて説明していきます。
単純グラフ
グラフを構成する点と点を結ぶ辺(多重辺)が複数個存在せず、自己ループ辺も存在しないグラフを言います。
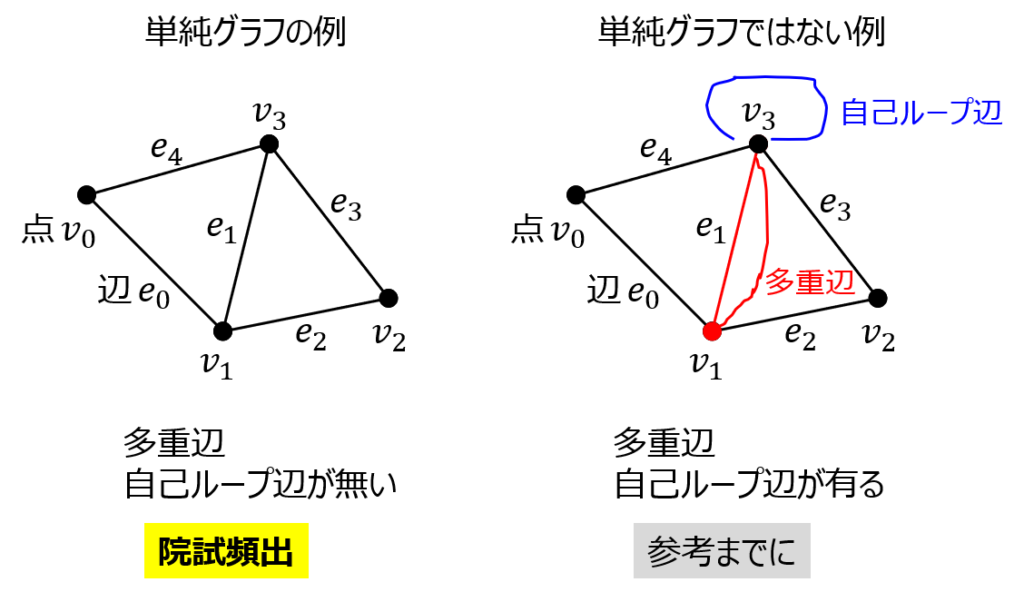
なお、多重辺が存在するグラフは多重グラフと呼ばれています。
院試問題でグラフ理論を出題する際は、無向グラフかつ単純グラフであることを暗黙の了解として作問することが多いです。
連結グラフ
グラフを構成する任意の点xと点yを結ぶ辺が存在することを言います。
直接xとyを結ぶ場合は勿論連結になりますが、別の点を経由するが、必ず最終地点yに至る道がある場合も連結になります。
要は、グラフが2つに分かれておらず、1つの塊になっているならば、そのグラフは連結であると言えます。
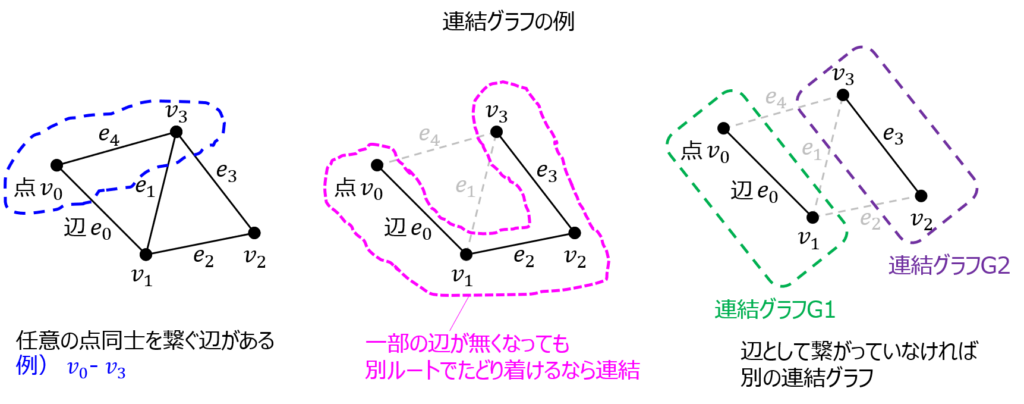
連結成分とは、グラフGを構成する塊の個数を意味しています。連結成分1のとき、グラフは分離しておらず、全て一つの塊になります。
院試では、問題の後半でよく問われます。
グラフの性質
点Vの個数がn個、辺Eの個数がm個である任意のグラフ\(G=(V,E)\)について、下記の関係が成立します。(多重グラフ含む)
握手定理
\(\deg(v)\)を、集合\(V\)に属するある点\(v\)に接続する辺の次数(本数)とすると、次数の総数は辺の個数の2倍と等しいです。
\begin{aligned}\sum _{n\in V }\deg \left( v\right) =2m\end{aligned}
証明
ある点\(v\)について、辺が\(\deg(v)\)本出ているとする。
それぞれの辺に対し、2本の点が必ず存在し、これが全ての点に対しても成立することから式(2)は証明できた。
奇数次の点の総数は偶数個存在する。
グラフ上の各点から伸びる辺の数は、偶数次、奇数次の2通りに分けられます。
偶数次の辺の場合、総数が奇数、偶数に依らず、(2)式の右辺は必ず偶数(2k)になります。
もし、奇数次の点の総数が奇数個の場合、右辺は奇数(2k’+1)になります。
両者を足しあわせると、右辺は奇数となってしまい、矛盾します。
よって、奇数次の点の総数は偶数個である必要があります。
十分性についても、同様に示すことができます。
単純グラフの性質
グラフを構成する点の最小次数が2以上ならば、Gには閉路が存在する。
背理法を用いて証明します。
閉路が存在しないと仮定するが、そのようなグラフは存在しないことを説明していきます。
具体的には、グラフが連結である場合、長さn-1の点が存在することに注目します。
証明
グラフGを構成するある点\(v_{0}\)について、最低次数が2なので、辺で結ばれている点\(v_{1},v_{2}\)が存在する。
よって、長さ2の道\(v_{0},v_{1},v_{2}\)が存在する。
長さn-1の道\(v_{0},v_{1},\cdots,v_{n-1}\)がグラフGの一部にあるとする。各点の次数は最低でも2以上のため、もし\(v_{n-1}\)が他の点\(v_{0},v_{1},\cdots,v_{n-2}\)と2つ接続するとき、閉路ができ、仮定と反する。
よって、\(v_{n-1}\)と接続する点の1つは\(v_{n}\)は\(v_{0},v_{1},\cdots,v_{n-1}\)に存在する必要がある。
しかし、この操作を繰り返すと、道の長さが∞に発散する。(矛盾)
以上より、閉路は存在する。
辺の個数mは、点の個数nに対し\(m≦n(n-1)/2\)以下である。
これは、単純グラフに対して成立します。前節の関係までは、多重グラフに対しても成立していましたが、ここからは別です。
証明
(2)式を変形し
\begin{aligned}m=\dfrac{1}{2}\sum _{n\in V }\deg \left( v\right)\end{aligned}
単純グラフのとき、任意の点vの次数は、点の個数nに対し自身の点を引いたn-1個までなので
\begin{aligned}\deg(v)≦n-1\end{aligned}
これを(3)式に代入することで
\begin{aligned}m≦\dfrac{1}{2}\sum _{n\in V }(n-1)=\dfrac{n(n-1)}{2}\end{aligned}
点の次数は、点の個数nに対し1つ引いた値が最大である考え方は、情報数学に限らずよく使います。
例えば、アルゴリズム論の最小全域木の計算時間を考えるうえでも、探索時間として辺の個数が影響してきます。
このとき、(4)式の関係を頭に抑えておくと、オーダー計算がスムーズにできます。
n≧2のとき、グラフG内には次数が等しい2点が存在する
証明
(4)式より、グラフ上の各点vについて、存在可能な次数は、\(0,1,2,\cdots,n-1\)
もし、ある点の次数がn-1\のとき、自身の点以外全てと辺で繋がる。よって、グラフ全体で見ても次数0の点は存在しないことが分かる。
逆に、次数0の点が存在するならば、次数n-1の点は存在しない。
よって、グラフGの各点で存在可能な次数の組み合わせは、下記の2通り考えられる。
\begin{cases}0,1,2,\cdots,n-2 \\ 1,2,3,\cdots , n-1\end{cases}
いずれの場合でも、n個ある点のそれぞれの次数はn-1個の値から取られる。
よって、少なくとも2つの点の次数は等しくなることが分かる。
連結グラフの性質
グラフGを構成する任意の点vの次数が\(\deg(v)≧(n-1)/2\)のとき、Gは連結である。
グラフGが単純グラフであることが前提です。
感覚的に、各点の次数がグラフを構成する点の総数nに1を引いた(n-1)/2以上ならば、辺を繋ぐ相手の辺の次数も含めてn-1以上になるので、連結になるだろうと予想できます。
数学的に証明すると、以下になります。
証明
グラフGに存在する連結成分の数をkとする。前提条件より
\begin{aligned}\deg(v)≧(n-1)/2\end{aligned}
点の数は、頂点の数より1つ多い。よって、各連結成分の点の個数\(m_{k}\)は
\begin{aligned}m_{k}≦\dfrac{n-1}{2}+1=\dfrac{n+1}{2}\end{aligned}
グラフを構成する点の数はnなので、連結成分の数もこの数以下になる。
\begin{aligned}k*\dfrac{n+1}{2}≦n\end{aligned}
これを変形し、
\begin{aligned}k≦\dfrac{2n}{n+1}=2-\dfrac{2}{n+1}\end{aligned}
kは1以上ないとグラフとして存在できなくなる。また、グラフを構成する点nは2つ以上無いと、辺が作れず、これもグラフとして成立しない。
n=2を上式に代入すると
\begin{aligned}1≦k≦\dfrac{4}{3}\end{aligned}
これより、\(k=1\)が成立し、前提条件を満たすとき、どのグラフも連結成分が1であることが分かった。つまり、グラフは分割しておらず、一つの塊である。
\(G_{1},G_{2}\)をグラフGの異なる連結成分のとき、\(G_{1},G_{2}\)は共有点を持たない。
証明
異なる連結成分=分離されたグラフであることから、互いのグラフは共有点を持ちません。
同様に、分離されたグラフを結ぶ辺も存在しません。
感覚的に理解しやすく、上記で十分と考えます。数学的な証明はここでは割愛します。(ただ、試験で問われた際は数式をしっかり用いましょう。)
\(G_{1}\)をGの任意の連結部分グラフとし、\(G_{2}\)をGの連結成分のとき
\(G_{1}\)と\(G_{2}\)が共有点を持つならば、\(G_{1} \subseteq G_{2}\)である。
証明
\(G_{1},G_{2}\)が共通の点\(v\)を持つとし、集合\(G’\)を下記のように置く。
\begin{aligned}G’=G_{1}\cup G_{2}\end{aligned}
\(G’\)上の任意の点(x,y)について両者をつなぐ道があることを示せば良い。
\((x,y)\in G_{1}\)および\((x,y)\in G_{2}\)のときは、それぞれ連結である前提なので、道は存在する。
\(x \in G_{1}\)、\(y \in G_{2}\)のとき、\((x,v) \in G_{1}\)で、\((v,y) \in G_{2}\)のため、(x,y)を繋ぐ道(x,v,y)が存在する。
よって、\(G’\)は連結であるが、\(G_{2}\)はGの連結成分として極大であるため、\(G’=G_{2}\)
以上から、\(G_{1} \subseteq G_{2}\)である。
グラフの行列表現、リスト表現
プログラミングを行う上で、グラフは行列表示、リスト表示し、コンピュータで計算できる形にすることが多いです。
行列表現
グラフを構成する各点に番号を振り、点と点の間が辺で結ばれている(隣接している)場合は、対応する行列の要素に1を設定する表記方法です。隣接行列とも呼ばれます。
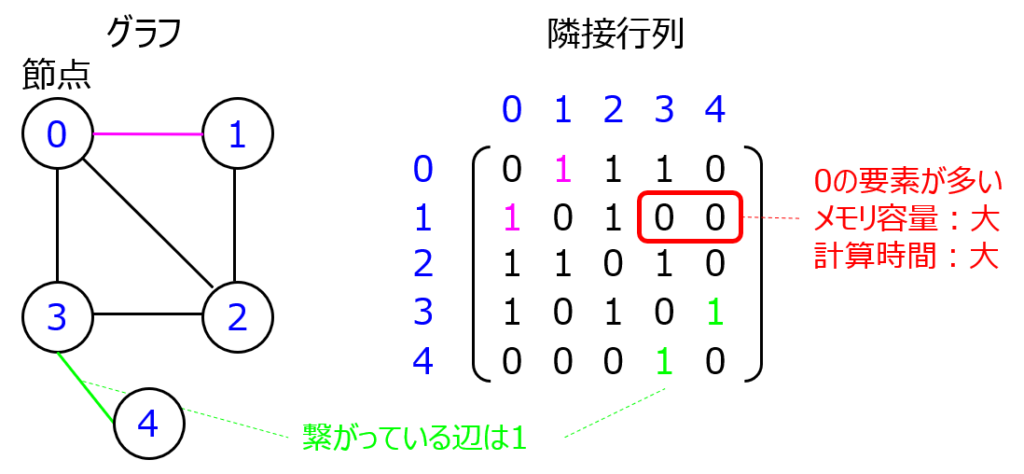
- 直感的であるため、人間の目で見ても点と点の関係が分かりやすい。
- 点同士が隣接しているとき、隣接行列に辺の重みを設定することで、コストも表現できる。
- 隣接していない要素に対し0を設定する必要があり、その分のメモリを消費する。
- 大規模なグラフを扱う場合、計算負荷が大きい。
リスト表現
グラフを構成する各点に対し、ポインタでリスト化し、接続関係を表す方法です。(隣接リストとも呼ばれます。)
この場合、接続している点同士のみをリストで対応すれば良く、隣接行列のようにメモリ負荷をかけることがありません。
一般的に、計算機でグラフを表現するときに最もよく使われる手法になります。

最後に
本記事では、グラフ理論の基礎が詰まっています。
数学的な証明として、集合を気にする必要があり、抽象的になることが多いです。じっくり練習し、自分のものにしましょう。