下記の微分方程式をべき級数を用いて解け。
(1)\(y’-2xy=x\)
(2)\(y^{”}-xy’+2y=0\)
微分方程式とは

微分項\(y^{”},y’\)が含まれた方程式を言います。
微分方程式を解くことにより、ある地点で発生している現在の出来事に対し、次に起こる出来事を求めることができます。(物理学的視点)
微分方程式には変数分離法など様々な型がありますが、直接計算して解を求める型と解を仮定して求める型の2通りに分かれます。
べき級数解法は、解を仮定して求める型になります。
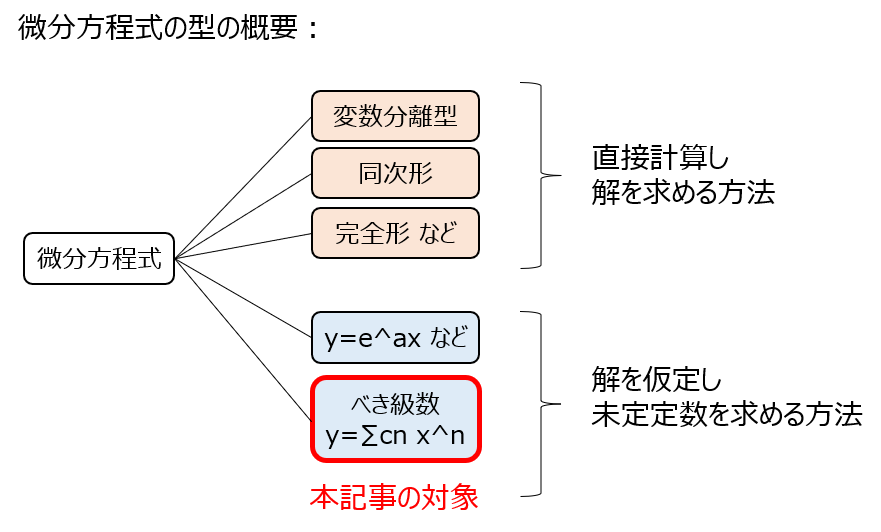
べき級数を用いた微分方程式の解き方
下記の手順で解いていきます。
- 与えられた微分方程式の通常点を求める。(後述)
- 通常点を\(x=x_{0}\)とすると、定数\(c_{n} \quad (n=0,1,\cdots) \)を用いて\(y=\sum ^{\infty }_{n=0}c_{n}\left( x-x_{0}\right) ^{n}\)で解を仮定できる。
- 仮定した解を微分方程式に代入し、未定定数\(c_{n}\)の関係式を求める。
- 最終的に求まった\(c_{n}\)を2.で仮定した式に代入することで、解が求まる。
多少計算が複雑になりますが、全体的な操作は\(y=e^{ax}\)を仮定するときと変わりません。
\(y=e^{ax}\)を与えられた微分方程式に代入。
未定定数\(a\)の値を求める。求めたaの値を\(y={ax}\)に適用し直すことで、解を求めていました。
級数型でも同じ手順で解を求めます。
通常点の求め方
文献を見ると難しいことが書かれていますが、まずは下記に注目すると良いです。
\begin{aligned}P_{0}(x)y^{”}+P_{1}(x)y’+P_{2}(x)=0\end{aligned}について、
\(P_{0}(x_{0}≠0)\)のとき、通常点
\(P_{0}(x_{0}=0)\)のとき、特異点
通常点のとき、\(y=y=\sum ^{\infty }_{n=0}c_{n}\left( x-x_{0}\right) ^{n}\)で解を仮定できる。
問題を解くうえではまず上記を知っておくことが重要です。もし、間違った点で級数展開すると、正しい解が求められなくなるからです。
問題を解くうえでの留意点
「微分方程式を解け」なる問題が院試で出題されたとき、これが変数分離型なのか、同次系なのか、完全微分方程式なのかを自力で判断することが多いです。
ただ、級数型については誘導が付いていることが多いです。(と言うか、ノーヒントで解く問題は今のところ見たことがありません。)
決められたルールで判別できないことが理由かもしれませんが、問題文の誘導に則って解く。を基本線に進めて良いと思います。
解答例
(1)\(y’-2xy=x\)
\(P_{0}(x)=1\)より、\(x=0\)は通常点である。
これより、\begin{aligned}y=\sum ^{\infty }_{n=0}c_{n}\left( x\right) ^{n}\end{aligned}と級数解を置ける。
(2)式を微分し、\begin{aligned}y’=n\sum ^{\infty }_{n=1}c_{n}\left( x\right) ^{n-1}\end{aligned}を得る。
(2)式(3)式を、与えられた微分方程式に代入すると
\begin{aligned}c_{1}+2c_{2}x+3c_{3}x^{2}+\cdots+nc_{n}x^{n-1}-2x(c_{0}+c_{1}x+c_{2}x^{2}+\cdots+c_{n}x^{n})=x\end{aligned}
上式より恒等式を立てると
\begin{cases}c_{1}=0 \\ 2c_{2}-2c_{0}=1 \\ 3c_{3}-2c_{1}=0 \\ 4c_{4}-2c_{2}=0 \\ … \\nc_{n}-2c_{n-2}=0 \end{cases}
\(c_{1}=0\)より、\(c_{3}=0\)。これが\(c_{5}\)以降も続くから、\(n\)が奇数の時は0。
\begin{aligned}c_{2k-1}=0 \quad (k=1,2,3…)\end{aligned}
\(n\)が偶数のとき、
\begin{aligned}c_{2}=\dfrac{1+2c_{0}}{2},c_{4}=\dfrac{1+2c_{0}}{2*2},c_{6}=\dfrac{1+2c_{0}}{2*3*2} \cdots \end{aligned}
以上から、任意の自然数\(k\)に対し
\begin{aligned}c_{2k}=\dfrac{1+2c_{0}}{2*k!}\end{aligned}
を得る。(6)式(8)式を(1)式に代入すると
\begin{aligned}y&=c_{0}+\dfrac{1+2c_{0}}{2}\sum ^{\infty }_{n=1}\dfrac{x^{2n}}{n!} \\ &=c_{0}+\dfrac{1+2c_{0}}{2}\left(\sum ^{\infty }_{n=0}\dfrac{x^{2n}}{n!}-1\right)\end{aligned}
ネイピア数の定義式
\begin{aligned}e^{x}=\sum ^{\infty }_{n=0}\dfrac{x^{n}}{n!}\end{aligned}
を(9)式に適用すると
\begin{aligned}y=c_{0}+\dfrac{1+2c_{0}}{2}(e^{x^{2}}-1)\end{aligned}
が与えられた微分方程式に対する一般解になる。
(2)\(y^{”}-xy’+2y=0\)
(1)と同じく、\(P_{0}(x)=1\)より、\(x=0\)は通常点である。
これより、\begin{aligned}y=\sum ^{\infty }_{n=0}c_{n}x^{n}\end{aligned}と級数解を置ける。
\begin{aligned}y=\sum ^{\infty }_{n=2}n(n-1)c_{n}x^{n-2}\end{aligned}
だから、(2)(3)(12)式を与えられた微分方程式に代入し
\begin{aligned}2c_{2}+3*2c_{3}x+4*3c_{4}x^{2}+\cdots +(n+2)(n+1)c_{n+2}x^{n}\\-x(c_{1}+2c_{2}x+3c_{3}x^{2}+\cdots+nc_{n}x^{n-1})\\+2(c_{0}+c_{1}x+\cdots+c_{n}x^{n})=0\end{aligned}
下記の恒等式を得る。
\begin{cases}c_{2}+c_{0}=0 \\ 3*2c_{3}-c_{1}+2c_{1}=0 \\ 4*3c_{4}-2c_{2}+2c_{2}=0 \\ 5*4c_{5}-3c_{3}+2c_{3}=0 \\…\\ (n+2)(n+1)c_{n+2}-nc_{n}+2c_{n}=0\\ \end{cases}
\(12c_{4}=0\)なので、\(k=1,2,\cdots \)に対し
\begin{aligned}c_{2k+2}=0\end{aligned}
\(c_{3}=-\dfrac{c_{1}}{3*2},c_{5}=\dfrac{c_{3}}{5*4}=-\dfrac{c_{1}}{5*4*3*2}\)と展開できることから、同じく\(k=1,2,\cdots \)として
\begin{aligned}c_{2k+1}=-\dfrac{1*3*5\cdots(2n-3)}{(2k+1)!}c_{1}\end{aligned}
を得る。(16)(17)式を(12)式に代入すると
\begin{aligned}y&=c_{0}+c_{1}x+c_{2}x^{2}+\sum ^{\infty }_{n=1}c_{2n+1}x^{2n+1} \\ &=c_{0}(1-x^{2})+c_{1}\left(x-\sum ^{\infty }_{n=1}\dfrac{1*3*5\cdots(2n-3)}{(2k+1)!}\right)\end{aligned}
が与えられた微分方程式に対する一般解になる。