【線形代数】行列のn乗の計算問題

はじめに

行列のn乗を求めるには、固有値を用いて対角化を行うことが多いです。この方法については、イレギュラーケースも含めてこちら1、こちら2の記事で説明しています。

本問も上記の考え方で解くこともできます。しかし、nをある値にして計算(実験)し、規則性を見つけることで答えを出すことも可能です。また、そのほうが時間がかからないケースもあり、本問がそれに該当します。

ちなみに、本問の行列はパウリ行列と言います。ただ、知らなくても問題ありません。

本記事で身に着けたいこと

「規則性」について、条件を明確に言語化することが難しいです。しかし、本問のようにある要素の転置成分のみ1で他は0になっている場合。上三角行列の場合、などは実験してみる価値ありです。

パウリ行列の話について、後述する解答例のネタバレと化していますが、実験してみると上記になることが分かります。実際に次の章で行ってみます。

実験から推測できる事実と解答例

実験

まず、2*2行列$A=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$を考えます。

このとき、$A^2=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=E$で、確かに単位行列であることが分かりました。

続いて、3*3行列$A=\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right)$でも試してみます。

このとき、$A^2=\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right)\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)=E$で、同様に単位行列になることが分かりました。

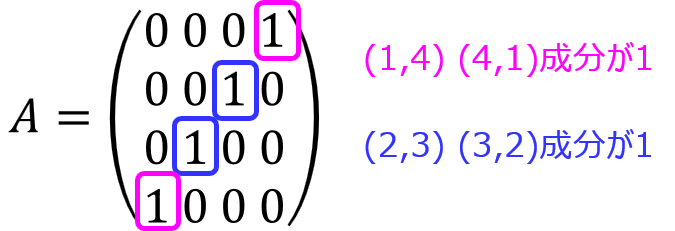
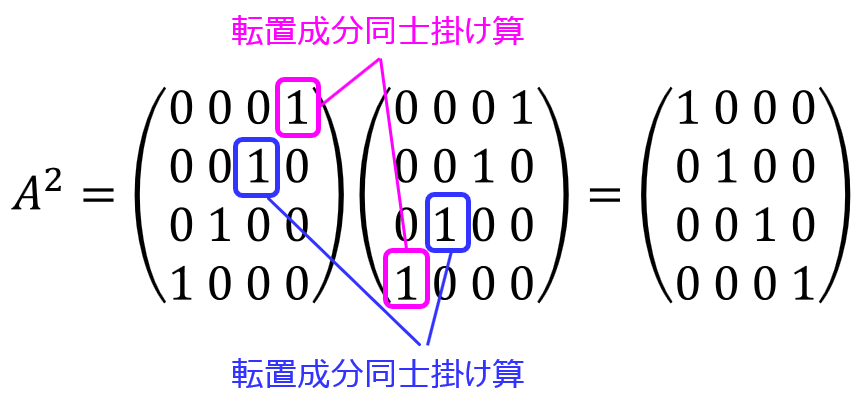
結局、Aのある要素(i,j)が1の場合、その転置成分(j,i)も1になっていることが分かります。この計算が発生する場合のみ1が立つことが分かります。この計算が発生する条件が、$A^2$の対角成分を求めるときにのみ発生します。こちらに気づくかどうかがポイントになります。・・・(*)

解答例

前節の(*)の考察から、任意のn次行列の2乗は単位行列$E$となる。

このことから、$A^3=A^{2}A=EA=A$、$A^4=A^2{A}^2=EE=E$になる。

よって、$n=2k-1(k=1,2,\dots )$ nが奇数のとき、$A^n=A^{2k}A=A$

$A^n$のnが偶数のとき、$A^n=A^{2k}=E$になることが分かる。

最後に

本問は、固有値を$\lambda$から式変形して求めようとすると、計算に時間がかかります。(行基本変形次第では上手い計算があるかもしれませんが･･･)

与えられた行列に規則性が見受けられないときは、素直に対角化を考えたほうが良いです。しかし、本問のように特徴的な行列を扱う場合は、実験してみるとそのほうが早いかもしれません。

参考文献

パウリスピン行列の性質 - 物理とか

whyitsso.net