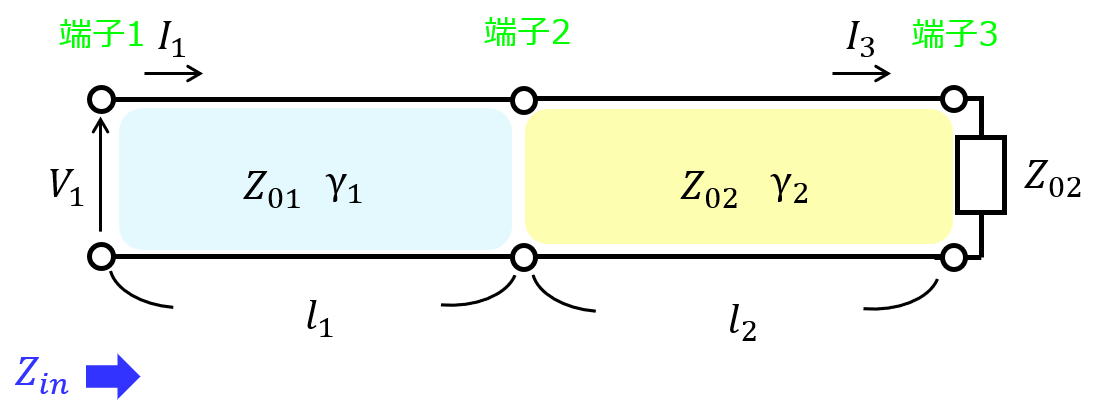
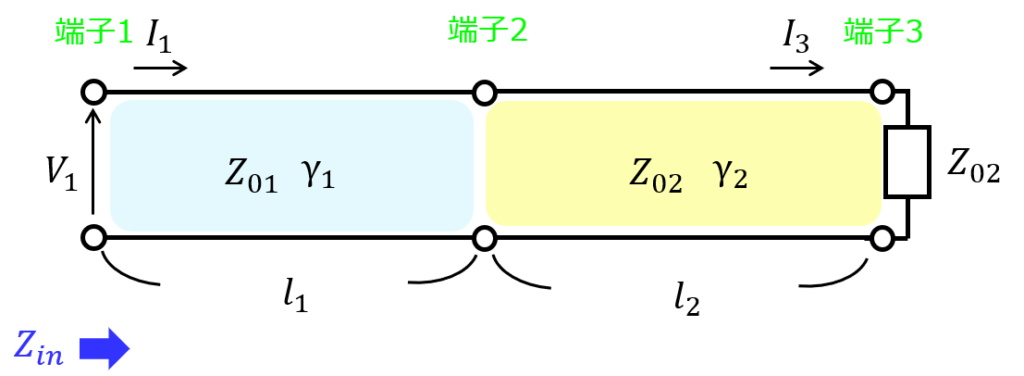
下記のように、端子2を境に特性インピーダンスが異なる分布定数回路を直列接続する。端子3を特性インピーダンス\(Z_{02}\)で終端したとき、端子1から見る入力インピーダンス\(Z_{in}\)を求めよ。なお、回路は無損失ではない。伝搬定数\(\gamma\)を使用し、F行列は双曲線関数で計算せよ。
はじめに
前回の記事では、端子2を境に線路が分岐した並列回路を解説しました。今回は、直列接続だが特性インピーダンスが途中で変わる回路について解説していきます。
どのような問題であれ、F行列を用いることが解法の起点になります。
この記事で覚えてほしいこと
- 分布定数回路も、直列接続の場合、F行列を掛け合わせることができる。
- 掛け合わせたF行列を元に、回路全体のF行列を求める。
- 終端抵抗の条件を代入し、入力インピーダンス\(Z_{in}\)を求める。
集中定数の二端子対回路問題で、下記のような回路を見かけたことはありませんか。
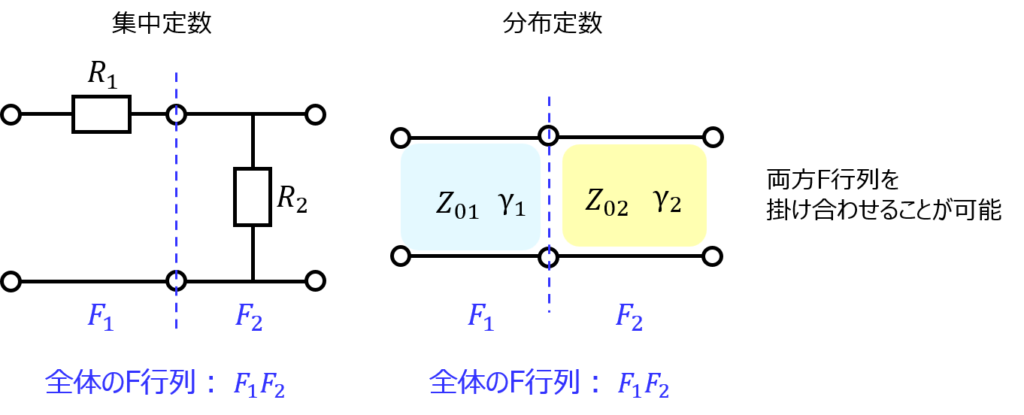
端子間のF行列が分かっていれば、それを掛け合わせることで全体のF行列が分かりました。
分布定数に関しても同じで、特性インピーダンスが切り替わる前後のF行列をそれぞれ求め、掛け合わせることができます。
全体のF行列\(F=\begin{pmatrix} F_{11} & F_{12} \\ F_{21} & F_{22} \end{pmatrix}\)が分かれば、後は下記の関係から入力インピーダンス\(Z_{in}\)を求められそうです。
\begin{eqnarray}\begin{pmatrix} V_{1} \\ I_{1} \end{pmatrix}=\begin{pmatrix} F_{11} & F_{12} \\ F_{21} & F_{22} \end{pmatrix}\begin{pmatrix} V_{3} \\ I_{3} \end{pmatrix}\end{eqnarray}
※\(V_{3}\)は端子3(出力端)にかかる電圧です。
解答例
全体のF行列
端子1-2間のF行列を\(F_{1}\)、端子2-3間のF行列を\(F_{2}\)とすると
\begin{eqnarray}F_{1}=\begin{pmatrix} \cosh \gamma_{1}l_{1}, & Z_{01} ,\sin h\gamma_{1}l_{1}, \\ \dfrac{\sinh \gamma_{1}l_{1}}{Z_{01}} & \cosh \gamma_{1}l_{1} \end{pmatrix}\end{eqnarray}
\begin{eqnarray}F_{2}=\begin{pmatrix} \cosh \gamma_{2}l_{2}, & Z_{02} ,\sin h\gamma_{2}l_{2}, \\ \dfrac{\sinh \gamma_{2}l_{2}}{Z_{02}} & \cosh \gamma_{2}l_{2} \end{pmatrix}\end{eqnarray}
なので、全体のF行列は、\(F=F_{1}F_{2}\)より
\begin{align}F&=\begin{pmatrix} \cosh \gamma_{1}l_{1}, & Z_{01} ,\sin h\gamma_{1}l_{1}, \\ \dfrac{\sinh \gamma_{1}l_{1}}{Z_{01}} & \cosh \gamma_{1}l_{1} \end{pmatrix}\begin{pmatrix} \cosh \gamma_{2}l_{2}, & Z_{02} ,\sin h\gamma_{2}l_{2}, \\ \dfrac{\sinh \gamma_{2}l_{2}}{Z_{02}} & \cosh \gamma_{2}l_{2} \end{pmatrix} \\ &=\begin{pmatrix} \cos \gamma_{1}l_{1}\cos h\gamma_{2}l_{2}+\dfrac{Z_{01}}{Z_{02}}\sin h\gamma_{1}l_{1}\sin h\gamma_{2}l_{2} & Z_{01}\sin h\gamma_{1}l_{1}\cos h\gamma_{2}l_{2}+Z_{02}\cos h\gamma_{1}l_{1}\sin h\gamma_{2}l_{2} \\ \dfrac{\sin h\gamma_{1}l_{1}\cosh \gamma_{2}l_{2}}{Z_{01}} +\dfrac{\cos h\gamma_{1}l_{1}\sin h\gamma_{2}l_{2}}{Z_{02}} & \dfrac{Z_{02}\sin h\gamma_{1}l_{1}\sin h\gamma_{2}l_{2}}{Z_{01}}+\cos h\gamma_{1}l_{1}\cos h\gamma_{2}l_{2} \end{pmatrix} \end{align}
入力インピーダンスの計算
前章の説明から、(1)式のF行列には(5)式の内容が入る。
\(V_{3}=Z_{02}I_{3}\)より、\(I_{2}\)を消去して\(Z_{in}\)を計算する。
\begin{align}Z_{in}&=\dfrac{V_{1}}{I_{1}} \\ &=\dfrac{Z_{02}\cosh \gamma_{1}l_{1}\left( \cosh \gamma _{2}l_{2}+\sinh \gamma_{2}l_{2}\right) +Z_{01}\sinh \gamma_{1} l_{1}(\cosh \gamma _{2}l_{2}+\sinh \gamma_{2}l_{2})}{ \dfrac{Z_{02}}{Z_{01}}\sin h\gamma_{1}l_{1}\left(\cosh \gamma _{2}l_{2}+\sinh \gamma_{2}l_{2} \right) +\cosh \gamma_{1}l_{1}\left( \cosh \gamma _{2}l_{2}+\sinh \gamma_{2}l_{2}\right)} \\ &= \dfrac{Z_{02}\cosh \gamma_{1}l_{1}+Z_{01}\sin h\gamma_{1}l_{1}} {\dfrac{Z_{02}}{Z_{01}}\sinh \gamma_{1}l_{1}+\cosh \gamma _{1}l_{1}} \\ &=Z_{01}\dfrac{Z_{02}+Z_{01}\tan h\gamma_{1}l_{1}}{Z_{02}\tanh \gamma_{1}l_{1}+Z_{01}} \end{align}
であることが分かった。
最後に
本問は、非常に計算が大変です。。
途中の計算ミスが怖いですが、防止するためのイメージだけ最後にお伝えします。
本問の条件だと、端子3が特性インピーダンス\(Z_{02}\)で終端されています。
この結果、端子2以降は無限長であるとみなせます。この結果、端子1から見ると端子2が特性インピーダンス\(Z_{02}\)で終端されているようになるため、\(\gamma_{2}\)は答えに出てこないです。
こういったイメージを掴んでおくことで、計算ミスを防ぐことができます。